RSA暗号で公開鍵と秘密鍵を生成する

RSA暗号とは

RSA暗号方式は公開鍵暗号方式における鍵の生成のアルゴリズムである。
巨大な2つの素数 $(p, q)$ の積 $pq$ が公開されているとき、その合成数 $pq$ から因数分解によって元の2組の素数 $(p, q)$ を求める難しさを安全性としている。本記事では小さな素数のペア $(p, q) = (97, 13)$ をもとに、RSA暗号方式による公開鍵と秘密鍵の生成の仕組みとデータの暗号化、送信、復号化の手順を図解する。また手計算が困難な場合はpythonを利用する。

公開鍵と秘密鍵の生成

公開鍵の生成

2組の素数$p, q$によって定まる定数値$n, \phi(n)$を次のように定める。

\begin{align}
 n &= pq　\\
 \phi(n) &= (p - 1)(q - 1)
 \end{align}

今回は $(p, q) = (97, 13)$ であるため

\begin{align}
n &= 97 \times 13 = \underline{1261} \\
\phi(n) &= 96 \times 12 = \underline{1152} \\
\end{align}

と計算され、$n = 1261, \phi(n) = 1152$と値が一意に決定する。nに関する関数$\phi(n)$は一般的に オイラー関数（Euler's function） もしくはオイラーのトーシェント関数（Euler's totient function）と呼ばれる。nが2つの素数$(p,q)$の積である場合のみ$\phi(n) = (p-1)(q-1)$と表すことができる。

次に定数$\phi(n)$と互いに素な正の素数を$e$を決定する。$\phi(n) = 1152$と互いに素であれば$e = 5$でも$e = 7$でもよい。説明の便宜上、ここでは$e = 5$とする。互いに素は2つの数の最大公約数が1であることを意味する。1152と5は最大公約数が1であるため、互いに素である。

ここまでの計算によって2組の素数$(p,q) = (97,13)$から$n = 1261, \phi(n) = 1152, e = 5$という3つの定数値を求めた。このうち$n = 1261$と$e = 5$はRSA暗号の公開鍵である。この公開鍵$(n, e)$はネットワーク上で公開する。nが今回は4桁という非常に小さい値であるため、この値1261から2つの素数$(p,q)$の組み合わせを第三者が特定するのは非常に簡単である。（$1261 = 97 \times 13$）実際の運用で利用される素数の組$(p, q)$はもっと巨大な素数のペアであり、それゆえ$n$も巨大な合成数となり、第三者がこの素因数分解をするのが困難になる。

公開鍵の生成のまとめ
1. 2組の素数$(p, q)$を決定する　$= (97, 13)$
2. $(n, \phi(n))$を計算する　$= (1261, 1152)$
3. 定数$e$を$\phi(n)$と互いな素な正の素数として決定$(= 5)$

秘密鍵の生成

秘密鍵を生成するために次の1次不定方程式を考える。

\begin{equation}
\alpha \cdot e + \beta \cdot \phi(n) = 1 \tag{1}
\end{equation}

今回の場合$\phi(n) = 1152, e = 5$であるから

\begin{equation}
5\alpha + 1152\beta = 1 \tag{2}
\end{equation}

という$\alpha$と$\beta$に関する一次不定方程式になる。これを満たす整数解$(\alpha, \beta)$は無数に存在する。任意の整数$k$として、この一般解は次のように表される。

\begin{equation}
\left\{ \, \tag{3}
    \begin{aligned}
     \alpha &= 461 - 1152k \\
     \beta &= -2 + 5k 
    \end{aligned}
\right.
\end{equation}

一次不定方程式の一般解の求め方は次回の記事で投稿する。
またこれからの説明の便宜上、この一次不定方程式の解$(\alpha, \beta)$を別の文字で次のように置き換える。

\begin{equation}
\left\{ \, \tag{4}
    \begin{aligned}
        d &:= \alpha \\
        x &:= -\beta
    \end{aligned}
\right.
\end{equation}

(4)式における等号記号（:=）は左辺式を右辺式で定義することを意味する。(4)式を元の(1)式に代入すると次の式を得る。

\begin{equation}
d\cdot e = x\cdot \phi(n) + 1 \tag{5}
\end{equation}

この式における整数$d$が秘密鍵となる。(5)式はRSA暗号方式の通信によるデータの完全性を証明するための重要な式である。Wikipediaに詳細が記載されていますので余力のある人のみ確認してみてください。完全性の証明

秘密鍵$d$を求めるために(3)式における任意の整数$k$を決定する。ここでは$k = 0$として$\alpha = 461$、$d = 461$という値を秘密鍵として採用する。

秘密鍵の生成のまとめ
1. 公開鍵を生成するときのパラメータ$(e, \phi(n))$を用いて次の1次方程式の一般解$(\alpha, \beta)$と特殊解1つ求める。

\alpha \cdot e + \beta \cdot \phi(n) = 1 \tag{*}

2.上の式の1つの特殊解$(\alpha, \beta) = (d, -x)$と置いて$d$の値を秘密鍵とする。

送信データの暗号化

データの準備

送信するデータとして次のファイルmessage.txtを用意する。

message.txt (テキストエディタでの表示)

I love you.

テキストエディタで表示すると上のように人間が理解できる文字列で表示される。このファイルをバイナリエディタという特殊なソフトで開くと16進数の数値データを確認することができる。

message.txt （バイナリエディタでの表示）

上の図において1文字に対して16進数2桁のコードが対応している。例えば先頭の'I'は0x49、スペースは0x20という16進数の値である。接頭辞0xはその数値が16進数であることを意味する。このアルファベッドの1文字/1記号と16進数の2桁の数値データの変換対応はASCIIコード表という表で定まっている。

16進数の2桁のデータ量は1バイトに相当する。上の図からmessage.txtは11文字分のデータがあるため、11バイトのファイルである。

暗号化の方針

公開鍵である$(n, e) = (1261, 5)$のうち$n = 1261$は非常に小さな値であるため、暗号化できる数値も非常に小さな値に限定される。ここでバイトの単位で表現できる数値の範囲は次のとおりである。

各サイズの数値の範囲
1バイト: 0～255
2バイト: 0～65,535
3バイト: 0～16,777,215

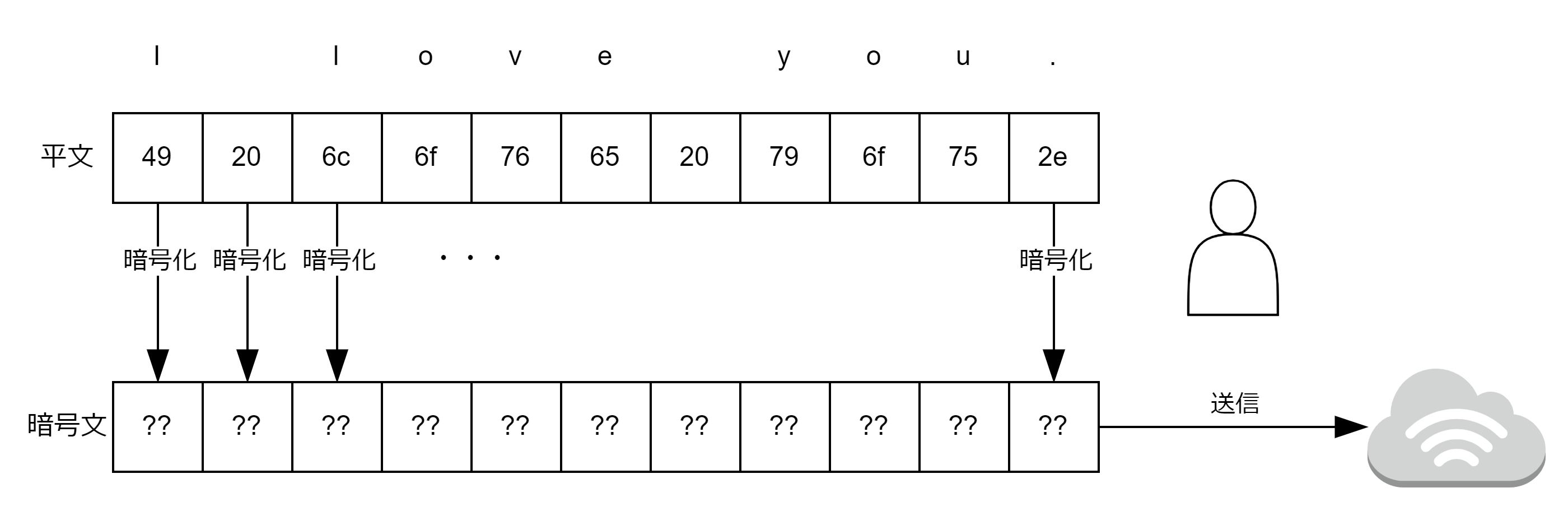
$n = 1261$を超えるデータを暗号化することができない。そのため、上の情報からmessage.txtのデータを暗号化する最小単位を1バイトにする。データの流れを図解すると次のようになる。

平文とは暗号化前のメッセージである。1文字分ごとに暗号化の処理を行い、ファイルの終端の文字まで暗号化が完了したものをインターネットで送るイメージである。

16進数表示の平文と10進数表示の平文の対応表の図を以下に示す。

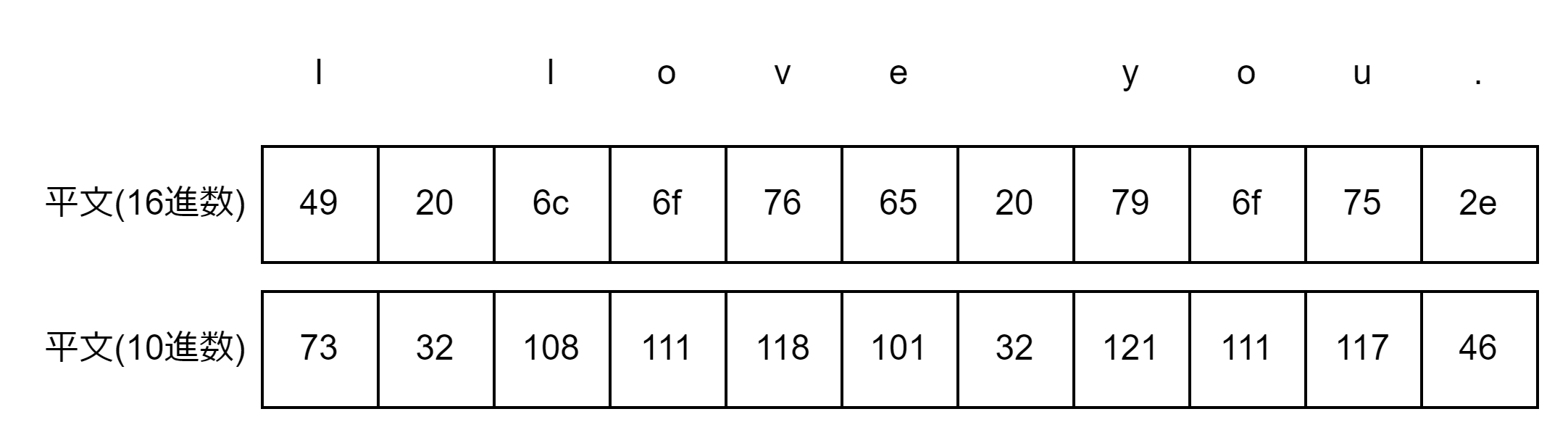
平文の文字列と暗号化後の文字列を配列で表すことにする。平文のメッセージを配列 a[] として、暗号化後のメッセージを配列 b[] とする。配列はプログラミング言語における記法でa[0] = 73, a[1] = 32, a[2] = 108, a[3] = 111, $\ldots$ ,a[10] = 46のように表す。
次の章でa[0]の値からb[0]の値を求める方法について図解する。

暗号化

一般的に公開鍵$(e, \phi(n))$を使い、平文$a$から暗号文$b$を求める式は次となる。

b \equiv a^{e} \mod{n} \ \ \in \mathbb{Z}_{n} \tag{6}

$\mathbb{Z}_n$は整数環$\mathbb{Z}$の中で$n$を法とした剰余類を表す。つまり$\mathbb{Z}_n$は0から$n - 1$までの整数の集合である（$0, 1, 2, \ldots n - 1$）。この条件により$b$の値は0以上$n - 1$以下という整数の範囲に限定される。(6)式に今回の公開鍵の値$(e,\phi(n))$を代入して(7)式を得る。

b \equiv a^{5}\mod{1261} \ \ \in \mathbb{Z}_{1261}  \tag{7}

具体的に計算してみる。a[0] = 73を(7)式の$a$に代入しb[0]を求めてみよう。modの記号と集合の記号は省略する。

\begin{align}
b[0] &\equiv a[0]^5 \\
&\equiv (73)^5 \\
&\equiv 203
\end{align}

73の5乗は計算したくない。数が大きくなってしまうからだ。合同式の性質を利用した剰余類を少ない計算量で求めるアルゴリズムが存在する。ここではpythonのターミナルコマンドを使い、以下のように計算した。

剰余類を計算する

>>> (73 ** 5) % 1261
203

上記の計算ではa[0]からb[0]を求めることができた。図で表現すると次のようなイメージである。

図の中の関数f(a)は(7)式の計算を表している。同様の計算手順でa[1]からb[1]、a[2]からb[2]、$\ldots$、a[10]からb[10]を求める。その結果を次の図に示す。

データの送信

具体的に暗号化されたメッセージがネットワークを通じて宛先まで届く順番を図として表現した。

上の図においてAさんがBさんに message.txt を送る。つまり、Aさんが送信者、Bさんが受信者である。RSA暗号は公開鍵暗号方式であり、送信者が受信者の公開鍵で暗号化する。Bさんが公開しているのは公開鍵の組$(e, n)$のみであり、秘密鍵$(p,q,d)$は自分だけの秘密にしておく。

送信者であるAさんは、平文であるファイルの中身をASCIIコード表を参照して数値データにする。次に数値データを前述の合同式の計算によって暗号化の配列を計算する。その後、ネットワークを通してBさんに暗号化したほうの文字列を送信する。

受信者であるBさんは、秘密鍵をもっているため、自分宛てに送られてきたメッセージを解読することができる。暗号化されたものを解読することを 復号化 と呼ぶ。この復号化の手順は次の章で図解する。復号化できるのは秘密鍵を持っているBさんのみである。ネットワーク中の経路で悪意のあるユーザがパケットの中身を盗み見た場合でも、秘密鍵を知らなければ元の平文を特定することができない。