Chainer Advent Calendar 2017の7日目です。
はじめに
みなさん、Deep Learningしてますか?正直Deep Learningって疲れますよね。パラメータチューニングの毎日、下がらないLoss、過学習するモデル、スタープラチナに殴られたようなGANで生成された大量の顔。
そんな鬱憤を晴らすべく、今日はChainerでDeep Learningをしない、という記事を書きます。
Computer Visionの多くの問題は、何らかの最小化問題として定式化されます。最小化する際は、殆どの場合は式を立て、微分し、最適なパラメータを求めます。そこには大きな問題があります。
微分めんどい
微分が複雑・・・式が複雑だと計算間違える・・・手法を変更するたびに微分しなくてはいけない。そんな問題を解決する凄いライブラリがあるのです。そう、Chainerです。Chainerではニューラルネットしか解けないと思っていませんか?
そんなことはありません。Chainerを使えばこの世の全ての問題が解けるのです。
ということで、本日は、3次元点群のマッチング、写真からの3次元復元、SLAMの問題、をChainerで解いてみることにします。なお、本日のコードはここに置きました。
ちなみに、最近は上記問題もDeep Learningで解こうという試みもありますが、今回はDeep Learningでは解きません。教師データとか軟弱なことはしません。また、後にも話題にでますが、単に自動微分につかってるだけじゃねーかというツッコミがあると思いますが、最近のDeep界隈の強い最適化もやってくれたり、GPUで計算できたりと、微分以外についても色々効果があります。
3D Point Registration
3次元点群をマッチングする手法として、ICPアルゴリズムが有名です。ICPアルゴリズムは、2組の点群同士で、同じ箇所の点同士を対応付け、対応間距離を最小にする点群の回転・並進パラメータを求める問題です。手始めに、この問題をChainerで解いてみましょう。本来はどの点同士が対応関係にあるかは未知のため探索問題を解いたりもしますが、今回は割愛することとします。
ここでは、3D点群界隈で最も有名なStanford Bunnyを対象に実験を行いましょう。同じ点群データを2つ用意し、それぞれの初期位置姿勢を下図のように設定します(なお、全く同じ点群というのもつまらないので、各点に対してランダムでノイズを与えておきます)。図のように位置がズレていることが分かります。今回はこの位置ズレを推定することとします。

定式化
はじめに、定式化をします。対応する3次元点を${\bf x}_i, {\bf y}_i$とし、${\bf x}$に対する回転行列を${\bf R}$、並進ベクトルを${\bf t}$とします。この場合、点群間の一致度合いは点間の距離の合計となります。従って、
\sum_i ({\bf y}_i - {\bf Rx}_i - {\bf t})^2
を最小化することで、点群のマッチングが行えます。
ここで、回転行列を含む最小化問題を解かなくてはいけないのですが、chainerには回転行列の微分は入っていません。そこで、回転行列の関数を書くことにします。回転行列の微分はその道の人でないと知らないと思いますので、簡単に解説します。回転行列${\bf R}$は、その転置行列${\bf R}^T$との行列積${\bf RR}^T$が単位行列${\bf I}$となり、かつ行列式$\left|{\bf R} \right| =1$を満たす3次特殊直交行列であり、回転群$SO(3)$をなします。
・・・という面倒な説明をするとボロが出るので、教科書に任せることとしましょう。結論のみ言うと、${\bf R}$は3x3行列の9個の要素を持ちますが、実際は3パラメータ$r_1, r_2, r_3$で構成され、回転行列の変換は、
G_1 = \left(
\begin{array}{ccc}
0 & 0 & 0 \\
0 & 0 & 1 \\
0 & -1 & 0
\end{array}
\right),
G_2 = \left(
\begin{array}{ccc}
0 & 0 & -1 \\
0 & 0 & 0 \\
1 & 0 & 0
\end{array}
\right),
G_3 = \left(
\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 0
\end{array}
\right)
と置いて、
{\bf R} = \exp \left( \sum_i {\bf G_i} r_i \right)
と書けます。上記計算は$\exp$が入ったりして一見意味不明ですが、ロドリゲスの回転公式と等しく、opencvのRodrigues関数で、3次元のベクトル${\bf r}$から回転行列${\bf R}$に変換できます。
さて、前置きが長くなりましたが、いよいよ微分です。$\exp$の微分は、その中身を外に出せば良いだけですので、
\frac {d{\bf R}}{dr} = \left( \frac {d}{dr} \sum_i {\bf G}_i r_i \right) \exp \left( \sum_i {\bf G_i} r_i \right)
と書けます。すなわち、$r_1$に関する微分の場合は、
\frac{d{\bf R}}{dr_r} = {\bf G}_1 \exp \left( \sum_i {\bf G_i} r_i \right) = {\bf G}_1 {\bf R}
と、非常に簡単に計算できます。結果として、$r_1$での微分は、${\bf G}_1$と、元のパラメータ$r_i$をRodrigues関数で変換して計算した${\bf R}$との行列積を取ればOKです。
これを元にchainerのルールに従ってrotation3d関数を書いてみます。
class Rotation3DFunction(function.Function):
def check_type_forward(self, in_types):
''' 省略 '''
def rodrigues(self, r, xp):
''' 省略 '''
def forward(self, inputs):
x = inputs[0]
r = inputs[1]
xp = cuda.get_array_module(*inputs)
rmat = self.rodrigues(r, xp)
y = x.dot(rmat.T).astype(x.dtype, copy=False)
return y,
def backward(self, inputs, grad_outputs):
x = inputs[0]
r = inputs[1]
gy = grad_outputs[0]
xp = cuda.get_array_module(*inputs)
rmat = self.rodrigues(r, xp)
gx = gy.dot(rmat).astype(x.dtype, copy=False).reshape(inputs[0].shape)
dR = xp.asarray([
[[0, 0, 0], [0, 0, -1], [0, 1, 0]],
[[0, 0, 1], [0, 0, 0], [-1, 0, 0]],
[[0, -1, 0], [1, 0, 0], [0, 0, 0]],
]).astype(r.dtype)
dRR = np.tensordot(dR, rmat, axes=((2), (0)))
dRRx = np.tensordot(dRR, x, axes=((2,),(1,))).transpose((2,0,1))
gr = np.tensordot(gy, dRRx, ((0,1), (0,2)))
return gx, gr
def rotation3d(x, r):
return Rotation3DFunction()(x, r)
という感じです。
rotation3d(x, r)
と呼び出すことで、3次元の回転を計算できます。
ネットワーク作成
通常はネットワークの重みをパラメータとして最適なパラメータを求めますが、今回はネットワークではなく、回転行列と並進ベクトルのパラメータを最適化します。勿論そのようなレイヤーはないので、EmbedIDを使うことにしましょう。なお、Biasレイヤーや、回転行列レイヤーを書いても良いですが、EmbedIDの方が別の問題でも同様に使えるので、こちらを使うことにします。教師データを${\bf y}$ とし、入力データ${\bf x}$とします。ネットワークのパラメータを$r, t$とします。以下のように実装しました。
class Net(chainer.Chain):
def __init__(self):
super(Net, self).__init__()
with self.init_scope():
self.embd = L.EmbedID(2, 3)
def __call__(self, x):
xp = chainer.cuda.get_array_module(x.data)
r = self.embd(xp.array([0], dtype=np.int32))
r = F.reshape(r, (3,))
t = self.embd(xp.array([1], dtype=np.int32))
t = F.broadcast_to(t, x.shape)
return rotation3d(x, r) + t
class loss_function(chainer.link.Chain):
def __init__(self, predictor):
super(loss_function, self).__init__(predictor=predictor)
def __call__(self, x, y):
py = self.predictor(x)
self.loss = F.mean_squared_error(py, y)
return self.loss
Netクラスで${\bf Rx}+{\bf t}$を計算し、loss_functionで教師データとのlossを計算しています。
実験結果
これを元に最小化すると、こうなります。

Chainerを使って点群のマッチングができる事を確認できました。めでたし。
余談ですが、回転群SO(3)以外(例えばホモグラフィ行列であればSL(3)、このへん参照)についても、$\exp$の出てきた式をテイラー展開して計算する事で、パラメータから行列への変換が求まります。ですので、今回はやりませんが、3次元の点群以外でも同様のアプローチで解けます。例えば、パノラマ画像作成などが可能となります。
ロバスト推定
さて、ここで終わっては勿体無い。なぜなら、上記は実はSVDをすれば解析的に解けてしまうからです。そこで、この発展系について解説します。このような最小化問題を解く際に、通常は外れ値を含むため、ロバスト推定が重要となってきます。ロバスト推定では2乗誤差を最小化する代わりに、L1ノルムを最小化したり、M推定をしたり、Huberノルムを最小化したりします。通常は、これらを最小化しようとすると、それぞれの微分を計算しなくては行けないのですが、Chainerを使えば、なんと微分を自動でやってくれます。例えば、L1ノルムにするのであれば、誤差関数を
loss = F.mean_absolute_error(py, y)
とするだけ。M推定の一つとして有名なtukeyのbiweight推定法であれば、
d = F.absolute(py - y)
D = xp.ones_like(d.data)
loss = F.sum((1-(F.maximum(D,d)/D)**2)**2)
とするだけ。Huber lossなら
d1 = F.absolute(py - y)
d2 = (py - y) ** 2
loss = F.sum(F.minimum(d1, d2))
とすれば良く、簡単にロバスト推定ができてしまいます。また、点と点の距離ではなく、面と点の距離の最小化を対象としても、同様に簡単に最小化できます。ここでは誤対応の可視化は結構難しく、しかもあまり画像としてインスタ映えしないので、実験結果は割愛しますが、ぜひ試してください。
Structure from Motion
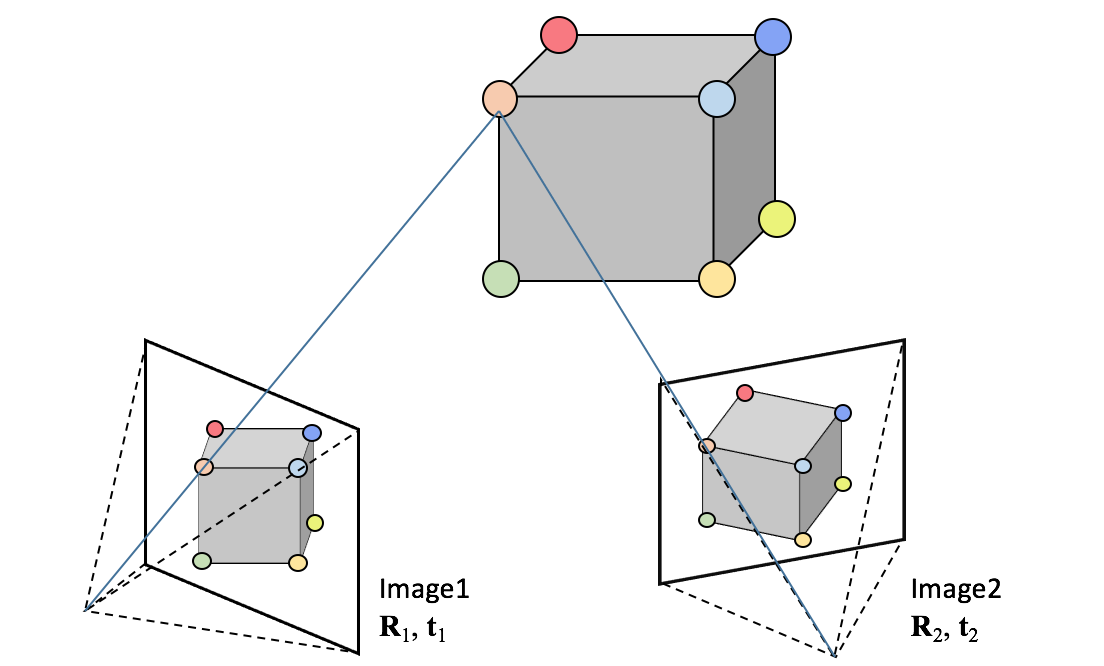
次のテーマはStructure from Motionです。Structure from Motionとは、簡単に言えば複数枚の2次元画像から3次元形状を復元する方法の事です。以下のように、3次元のオブジェクトを2箇所から撮影すると、それぞれの撮影地点の姿勢に応じて異なる見え方となります。この見え方と無矛盾となるような、カメラの姿勢と撮像対象の形状を求めます。
定式化
3次元点群のマッチング同様に、詳細な解説は他に任せることとして、ここでは式のみ記載します。3次元座標${\bf X}$の位置にある点は、姿勢${\bf R}$、${\bf t}$、内部パラメータ行列${\bf A}$のカメラ画像には、下記の座標$(u, v)$に写ります。
{\bf P} = {\bf A} \left[ {\bf R} \mid {\bf t} \right] \\
u = \frac{P_{11} X_1 + P_{12}X_2 + P_{13}X_3 + P_{14}}{P_{31}X_1 + P_{32}X_2 + P_{33}X_3 + P_{34}} \\
v = \frac{P_{21} X_1 + P_{22}X_2 + P_{23}X_3 + P_{24}}{P_{31}X_1 + P_{32}X_2 + P_{33}X_3 + P_{34}} \\
3次元復元をするために、推定するパラメータはカメラ$i$の姿勢${\bf R}, {\bf t}$と、画像上の特徴点$j$の3次元座標${\bf X}$となります。最小化では、推定すべき上記パラメータで3次元点がカメラのどの画素に写ったかを計算し、実際の撮影画像から得た値$(u, v)$と等しくなるようにします(なお、文中に添え字付きの数式を入れると表示がバグるようなので心の目で見てください)。撮影画像と、パラメータの誤差関数は
\sum_{ij} \left( u_{ij} - u({\bf R}_i, {\bf t}_i, {\bf X}_j) \right)^2 + \left( v_{ij} - v({\bf R}_i, {\bf t}_i, {\bf X}_j) \right)^2
となります。この式を最小化することで、カメラの姿勢と撮影対象の3次元形状が得られます。なおこの最小化をBundle Adjustmentと呼びます。Chainerを使わずにこの式を微分しようとすると、ここで導出されているように、かなり大変です。Chainerを使えば、この辺の導出から実装までをしなくてよいので、非常に楽になりますね。
ネットワーク作成
特に解説するところもないですが、姿勢パラメータと、形状を表す点群をEmbedIDとし、call時に点群が画面のどの位置に写るかを返します。loss関数で、実際に写った位置との差分である逆投影誤差を出力します。
class Net(chainer.Chain):
def __init__(self, matA, nb_data, rvec, tvec, points):
super(Net, self).__init__()
self.matA = matA.astype(np.float32)
embd = np.stack((rvec, tvec), axis=0)
pts = points.reshape(-1)
with self.init_scope():
self.embd = L.EmbedID(2, 3, initialW=embd)
self.points = L.EmbedID(1, 3 * nb_data, pts)
def proj(self, x):
xy, z = F.split_axis(x, (2,), axis=1)
r = xy / F.broadcast_to(z, xy.shape)
return r
def __call__(self):
xp = self.xp
matA = xp.asarray(self.matA)
pts = self.points(xp.array([0], dtype=np.int32))
pts = F.reshape(pts, (-1, 3))
p0 = F.matmul(pts, matA, transa=False, transb=True)
p0 = self.proj(p0)
r = self.embd(xp.array([0], dtype=np.int32))
r = F.reshape(r, (3,))
t = self.embd(xp.array([1], dtype=np.int32))
t = F.broadcast_to(t, pts.shape)
rxt = rotation3d(pts, r) + t
p1 = F.matmul(rxt, matA, transa=False, transb=True)
p1 = self.proj(p1)
return p0, p1
class loss_function(chainer.link.Chain):
def __init__(self, predictor):
super(loss_function, self).__init__(predictor=predictor)
def __call__(self, p0, p1):
q0, q1 = self.predictor()
self.loss = F.mean_squared_error(p0, q0) + F.mean_squared_error(p1, q1)
reporter.report({'loss': self.loss}, self)
return self.loss
実験結果
実験では、下記2枚の画像を対象として、SIFTで特徴点の検出・マッチングを行います。マッチング結果は上位100件の対応のみ表示します。


2画像の場合、姿勢と形状に関して近似による解を持つので、それを初期値とします。OpenCVの機能で実行でき、以下のようにして姿勢と形状を求めます。
# Estimation of essential matrix and decomposition to pose
E, mask = cv2.findEssentialMat(p0, p1, matA, method=cv2.RANSAC, prob=0.999, threshold=3.0)
_, rmat, tvec, _ = cv2.recoverPose(E, p0, p1)
rvec, _ = cv2.Rodrigues(rmat)
# traiangulation
pl = np.dot(matA, np.eye(3, 4, dtype=np.float32))
pr = np.dot(matA, np.concatenate((rmat, tvec.reshape(3,1)), axis=1))
point4d = cv2.triangulatePoints(pl, pr, p0.T, p1.T).T
point3d = (point4d[:] / point4d[:,3:])[:,:3]
これを初期状態として、姿勢と形状をRefineすると以下のような点群が得られます。なお、2画像だと十分な点群が得られないので、結果は正直いってショボいです。枚数を増やせば、より密な点群が得られるのですが、実装がめっちゃ大変なので、本記事ではここまでとします。

ここで特筆すべきは、最適化にAdamを使っている事です。本来、Bundle Adjustmentするためには、大規模な疎行列の逆行列を計算してMarquardt法などで収束させます。それには疎行列のソルバも必要になるので非常に大変です。これに対し、今回のサイズでしか試してはいないのですが、Adamを使ってみた所、容易に収束させられる事が分かりました。Chainerを使えばGPU化も簡単にできるので、既存の疎行列を使う方法より、メモリ効率・速度ともに良かったりするかもしれませんが、そこは要調査ですね。
Simultaneous Localization and Mapping
最後はSimultaneous Localization and Mapping (SLAM)です。SLAMとは、ロボットが周囲の形状を計測しつつ移動した場合に、自分の位置を推定しつつ、周囲形状の地図を作成する手法です。ロボットの問題ですが、これもこれまで同様に最小二乗の枠組みで解けるので、Chainerの出番です。SLAMといっても様々な種類があるのですが、ここではGraphSLAMの問題を扱ってみましょう。
実験環境について
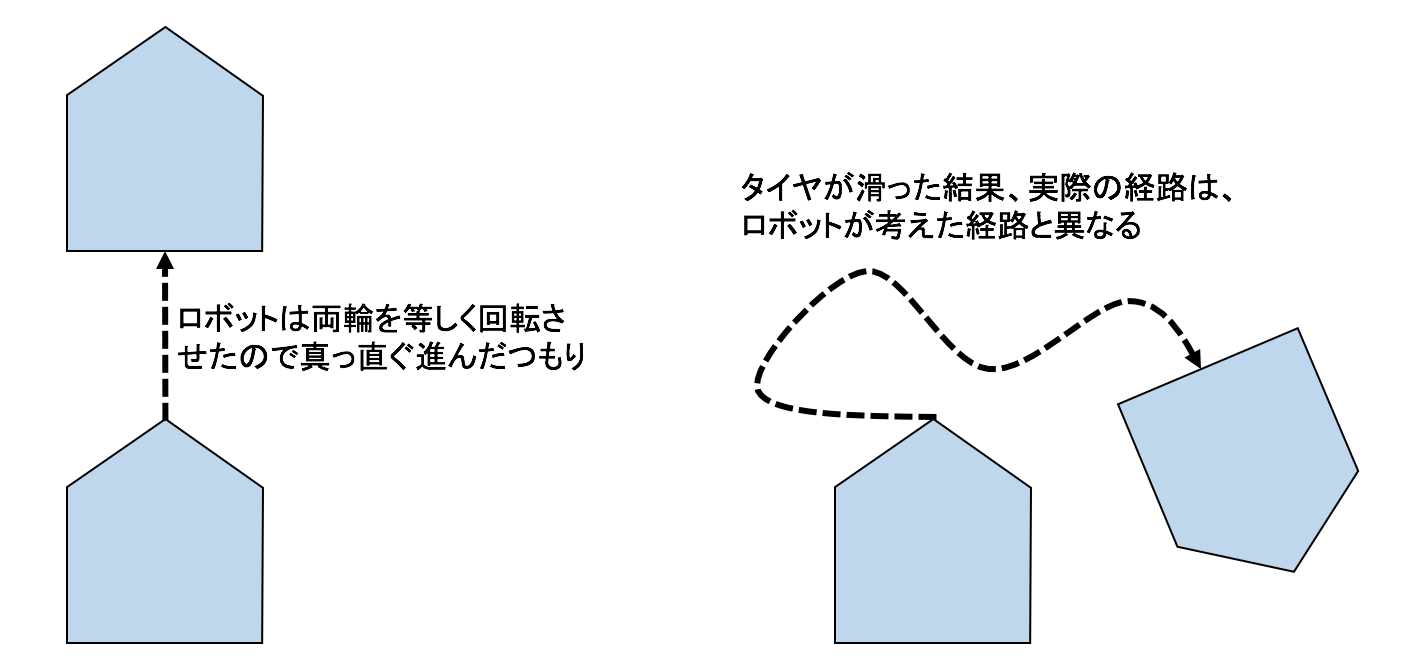
ロボットを実際に動かすのは大変なので、今回はシミュレーションで実験を行います。さて、ロボットは移動の際に、タイヤの回転数(オドメトリ)を記録して自分の経路を記録します。ところが、実際はタイヤの滑りがあるため、オドメトリのみで自分がどのような経路を通ったかを復元することはできません。イメージとしては以下のようになります。
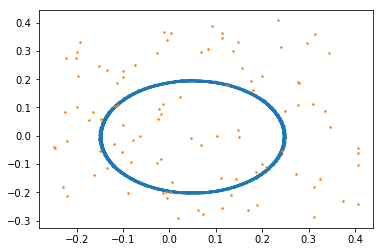
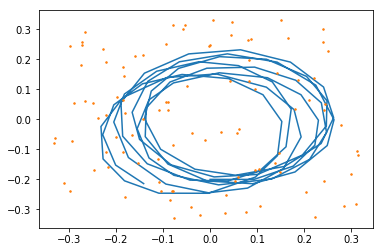
実験では、ロボットは一定のスピードで一定の範囲を回り続ける動作をすることとします。なお、シミュレーションではロボットが1ステップ進む度に、移動距離と変化角度にランダムに誤差を与えることとします。また、ランドマークの計測についても同様に誤差を与えることとします。ロボット自身に記録されたオドメトリと計測したランドマークから、経路とランドマークを復元したのが下記となります。
青い線がロボットの軌跡、オレンジの点が周囲の形状(ランドマーク)です。ロボットは、あるコースをグルグル回り続けていると自分では思い込んでいます。ところが、タイヤの滑りおよび計測誤差を持つため実際には上記図のようにはなりません。実際に走ったコース、配置したランドマークは下記であったとします。
上記のように、ロボットに記録された情報とは経路、ランドマーク位置共に異なっていることがわかります。今回はSLAMによって、ロボットに記録された情報から、実際の経路・ランドマーク位置を推定していきます。
定式化
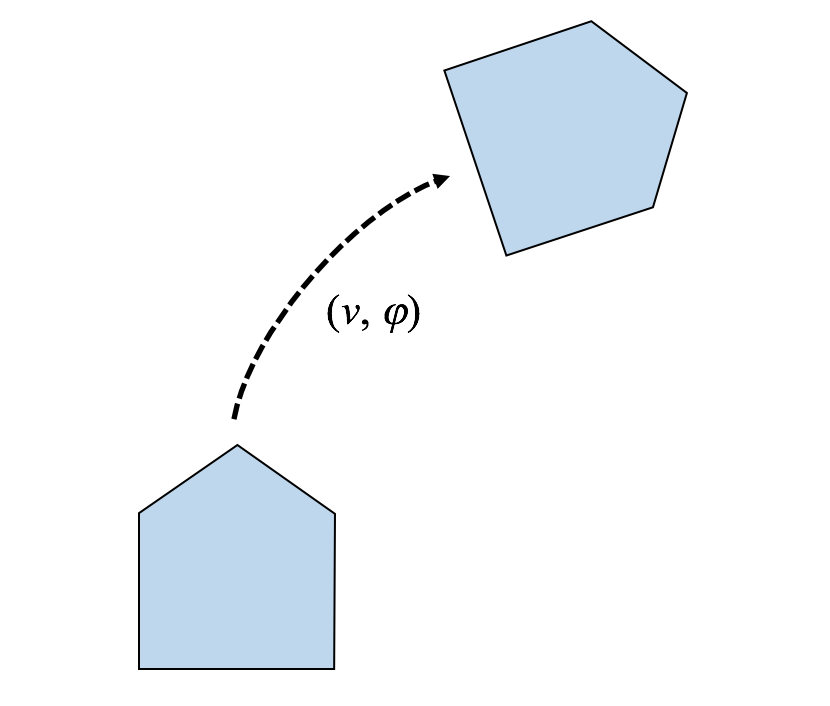
まず、ロボットの動作を定式化します。ここでは比較的簡単な回転と直進の動作を行えるロボットとします。ロボットが1ステップ動くと以下のように位置姿勢$x,y,t$が変化することとします。
x_{t+1}=x_{t} + v \cos (t_{t}) \\
y_{t+1}=y_{t} + v \sin (t_{t}) \\
t_{t+1}=t_{t} + \varphi
周囲の形状として、ここでは簡単のためポールが立っている事として、これをランドマークと見なし、ロボット$(x,y,t)$からランドマーク$(p,q)$までの相対距離・角度を計算することにします。
d=\sqrt{(m_x-x)^2+(m_y-y)^2}\\
\theta=\arctan (m_y-y, m_x-x) - t

SLAMでは、推定した結果が、ロボットに記録されたオドメトリ情報と、ランドマーク計測情報からなるべく離れないようにするのが目的となります。すなわち、下記の最小化が目的となります。
\sum_{t} \left( {\bf x}_{t} - g({\bf x}_{t-1}, {\bf u}_t) \right) {\bf V}^{-1} \left( {\bf x}_{t} - g({\bf x}_{t-1}, {\bf u}_t) \right)^T + \\
\sum_{ti} \left( {\bf z}_i - h({\bf x}_{t}, {\bf m}_{ti}) \right) {\bf Q}^{-1} \left( {\bf z}_i - g({\bf x}_{t}, {\bf m}_{ti}) \right)^T
なお、$g({\bf x}, {\bf u})$は、姿勢${\bf x}$のロボットがオドメトリ${\bf u}$として移動した場合の移動結果の姿勢とします。また、$h({\bf x}, {\bf z})$は、姿勢${\bf x}$のロボットが位置${\bf m}$にあるランドマークを計測した場合の、計測結果とします。${\bf V}$と${\bf Q}$は、それぞれオドメトリと計測に関する誤差の共分散とします。
ネットワーク作成
今までと異なり多少複雑になってきます。理由としては、ロボットのステップと、計測の2つのモジュールがある事や、角度の差分を出力するため1周回ったかどうかを判定する必要があるからです。まず、全体から見ていきましょう。callの前半はロボットの1ステップ、後半は計測を行います。idxは時刻tを表します。最後はそれらの合計をlossとして出力します。
class Net(chainer.Chain):
def __init__(self, pose, landmark, R, S):
super(Net, self).__init__()
self.R = R
self.S = S
self.nb_pose = len(pose)
self.nb_landmark = len(landmark)
with self.init_scope():
self.pose = L.EmbedID(self.nb_pose, 3, initialW=pose)
self.landmark = L.EmbedID(self.nb_landmark, 2, initialW=landmark)
def step(self, pos, odm):
'''省略'''
def observation(self, pos, lm):
'''省略'''
def diff_theta(self, d):
'''省略'''
def __call__(self, idx, odm, obs):
xp = self.xp
#
p0 = self.pose(idx-1)
p1 = self.step(p0, odm)
q1 = self.pose(idx)
r = q1 - p1
dxy, dr = F.split_axis(r, (2,), axis=1)
dr = self.diff_theta(dr)
r = F.concat((dxy, dr), axis=1)
#
idx = np.arange(self.nb_landmark, dtype=np.int32)
lm = self.landmark(idx)
z = self.observation(q1, lm)
s = obs - z
dlen, dt = F.split_axis(s, (1,), axis=2)
dt = self.diff_theta(dt)
s = F.concat((dlen, dt), axis=2)
s = F.reshape(s, (-1, 2))
self.loss = F.sum(F.matmul(r, R)*r) + F.sum(F.matmul(s, S)*s)
return self.loss
姿勢のステップ関数は以下となります。xyに関する更新と、tに関する更新が異なるので、split_axisして別々に計算した後にconcatします。
def step(self, pos, odm):
x, y, r = F.split_axis(pos, (1,2), axis=1)
u, v = F.split_axis(odm, (1,), axis=1)
x += u * F.cos(r)
y += u * F.sin(r)
r += v
return F.concat((x, y, r))
計測処理の関数は以下となります。時刻tにおいけるi番目のランドマークの計測結果を計算するため、次元が一つ増えるため少し複雑です。broadcast_toを使いつつ、次元数を合わせて計算していきます。
def observation(self, pos, lm):
xy, r = F.split_axis(pos, (2,), axis=1)
nb_pos = len(pos)
_lm = F.reshape(lm, (1, self.nb_landmark, 2))
_lm = F.broadcast_to(lm, (nb_pos, self.nb_landmark, 2))
_xy = F.reshape(xy, (-1, 1, 2))
_xy = F.broadcast_to(_xy, (nb_pos, self.nb_landmark, 2))
_r = F.reshape(r, (-1, 1, 1))
_r = F.broadcast_to(_r, (nb_pos, self.nb_landmark, 1))
d = _lm - _xy
length = F.sqrt(F.sum(d ** 2, axis=2, keepdims=True))
dx, dy = F.split_axis(d, (1,), axis=2)
t = myF.arctan2(dy, dx) - _r
回転に関する差分は、差異が±180度を超えたら、逆回りで差異を計算した方が正しく、fmodを利用しながら計算します。
def diff_theta(self, d):
d = F.fmod(d + np.pi, np.array([2*np.pi], dtype=np.float32)) - np.pi
d = F.fmod(d - np.pi, np.array([2*np.pi], dtype=np.float32)) + np.pi
return d
実験結果
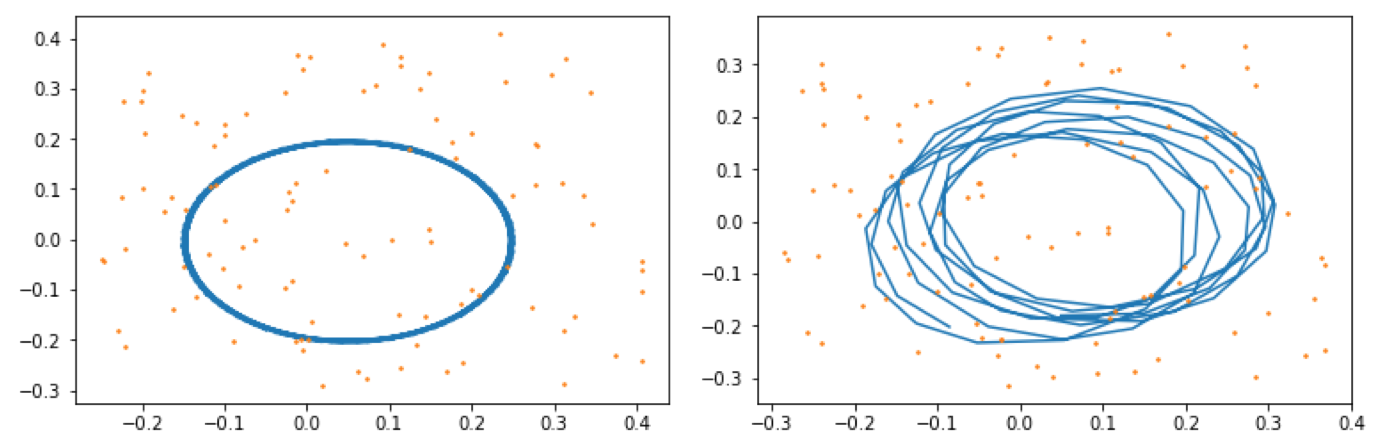
結果が分かりづらいので、先に誤った経路・地図(左)とGround Truth(右)を再掲します。
これを最適化した結果下記になります。
きちんとロボットが通った経路やランドマークを推定できている事が確認できました!
終わりに
ChainerでDeep Learningをせず、他の用途に使ってみました。色々使える事が確認できましたし、Adamの効果など新しい知見も得られました。上記以外にも、式が定式化されていさえすれば、このほかにも色々使えると思います。