Chainer Advent Calendar 2017の17日目です。
はじめに
枠に空きができたので、最近の実装して見た論文の簡単な解説と結果を紹介します。今日も今日とて、人の褌で相撲を取っていこうと思います。
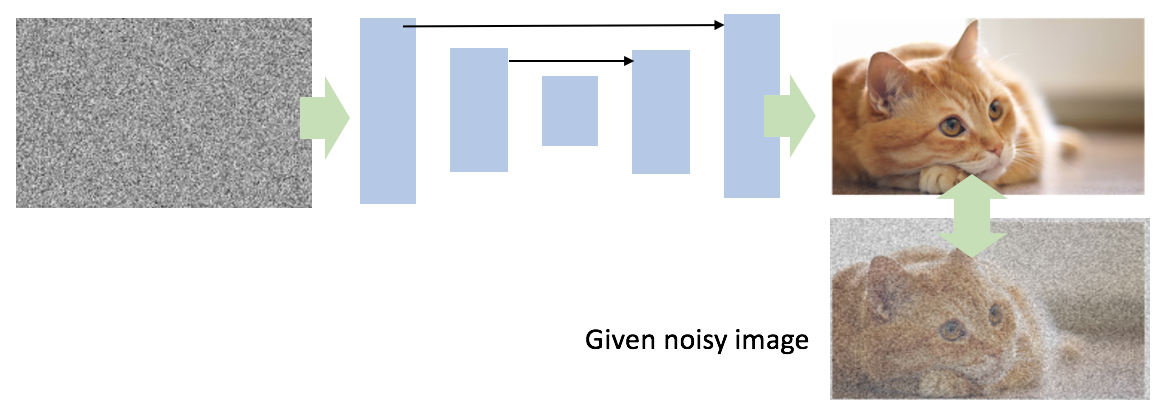
今日紹介する論文は「Deep Image Prior」というものです。画像処理の基本タスクとして、ノイズ除去・超解像・インペインティングなど、色々な手法が研究されていますが、Deep Image Priorは、これらのタスクに汎用的に使える中々便利なテクニックです。
以下の図が著者の論文で扱われているタスク群です。色々使えてすごいですね。
ということで、本日はこれを実装していきましょう。
前提知識
上記に挙げた画像処理群は、基本的には以下の式を最小化することで行われます。
x^* = \min_x E(x;x_0) + R(x)
$x_0$は元の画像であり、例えばノイズなどを含む画像、$x$は生成画像とします。$E$は元の画像と処理後の生成画像の一致度、$R$は画像が自然かどうかの指標です。後者の指標が必要な理由は以下です。Eのみを最小化すると生成画像が元の画像と一致しますが、するとノイズを含んだ不自然な画像になります。そこで、$R$は自然っぽさ、すなわちノイズが無いような画像であれば値が小さくなります。$R$を用いることで、元の画像を維持しつつ、ノイズが無い画像が生成されます。
以下の画像は、もっとも左がノイズを含む画像$x_0$で、もっとも右はノイズの一切ない自然な画像を示します。このバランスを取った良いところを探すことで、ノイズを除去できます。
さて、この場合、何を以って自然とするかの指標を作るのが難しいと言うのが課題です。これまでも、以下の表に示すように様々な研究がされてきましたが、十分な指標がないのが現実です。
Deep Image Prior
概要
さて、この問題を解決しようというのがDeep Image Priorです。Deep Image Priorとは、画像$x$をニューラルネットワークで生成する事で、ニューラルネットワーク自体が自然な画像を生成できる能力を持っている為に、陰的に先ほどの制約を満たす画像が生成される、というものです。簡単に言うと、ニューラルネットワークで画像生成してみたら、何も考えなくても綺麗な画像が生成されちゃった、という中々驚きの手法なのです。
具体的には、綺麗にしたい画像$x_0$と、入力として与えるノイズ画像$z$を用意し、$z$から$x_0$に変換するネットワークパラメータ$\theta$を求めます。$f$はニューラルネットワークとします。
\theta^* = \arg\min_x E(f_\theta(z);x_0)
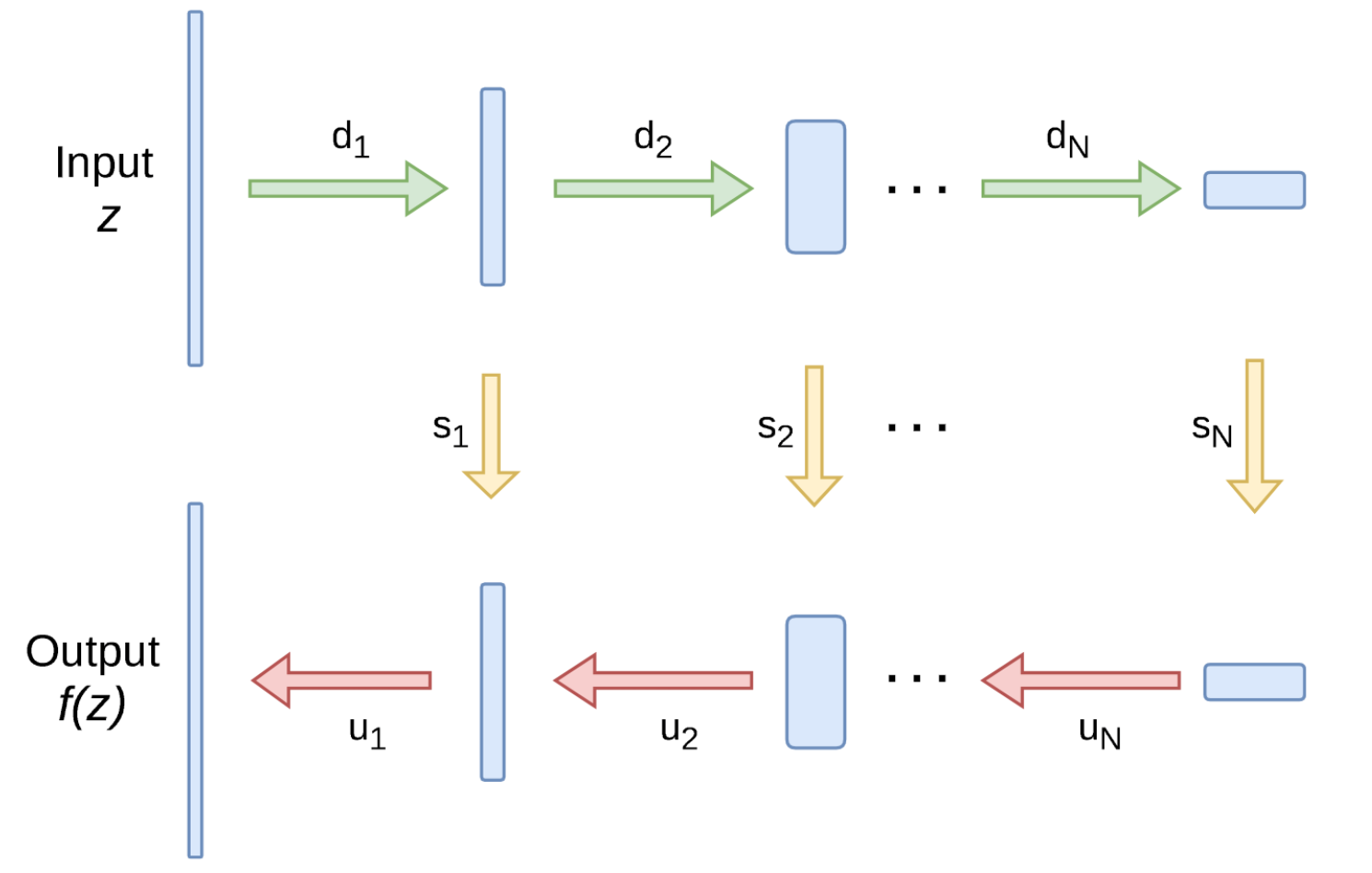
ネットワーク図にすると以下のような感じです。
動作する理由
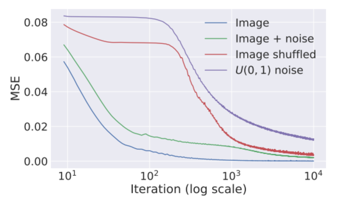
さて、ニューラルネットワークを使うと何故自然な画像が生成されるかですが、結局謎です。ただし、ノイズのようなランダムな画像と比べると、自然のような規則的な構造を持つ画像の方がニューラルネットワークで近似しやすいから、とのことです。実験として、自然画像とノイズ画像をそれぞれ生成しようとした時の学習速度を比較すると、自然画像の方がより簡単に学習できることがグラフで示されています。
青の線が自然画像を生成したケースで、100回程度パラメータを更新すれば、そこそこ元画像に近づいた結果を得られるのに対して、紫の線がノイズ画像を生成したケースでこの場合は10000回更新してようやく近似ができた、と言う結果になっています。畳み込み層は、線などの構造的なデータを表すのが得意という特徴がある為に、上記のような結果になるようです。なるほどー。
ネットワーク
ネットワークはダウンサンプリングモジュール($d_i$)とアップサンプリングモジュール($u_i$)及びU-Netのようなスキップモジュール$s_i$によって構成されます。入力は、固定したノイズ画像$z$となります。
ダウンサンプルモジュールは下記となり、Conv-Downsample-BN-Activation, Conv-BN-Activationで構成されます。
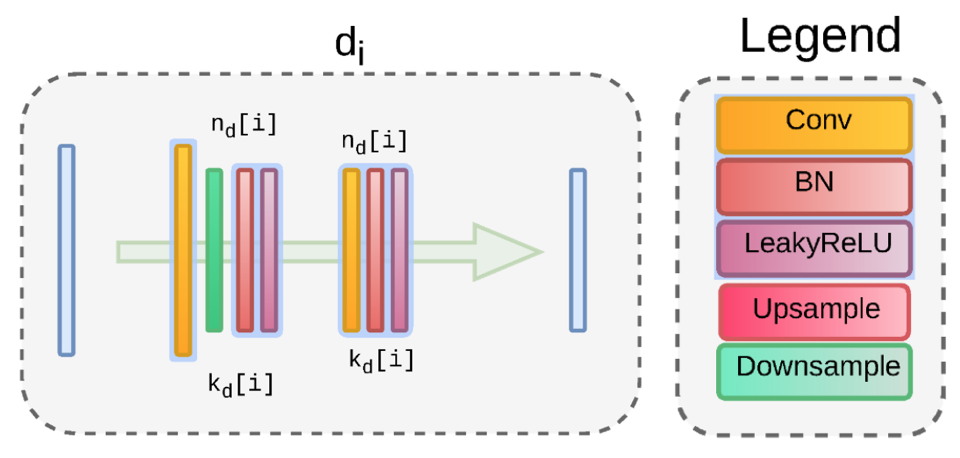
Chainerで書くと以下のようになります。
class DownsampleBlock(chainer.Chain):
def __init__(self, in_channel, out_channel):
super(DownsampleBlock, self).__init__()
with self.init_scope():
self.c1 = L.Convolution2D(in_channel, out_channel, 3, pad=1, stride=2)
self.b1 = L.BatchNormalization(out_channel)
self.c2 = L.Convolution2D(out_channel, out_channel, 3, pad=1)
self.b2 = L.BatchNormalization(out_channel)
def __call__(self, x):
h = F.leaky_relu(self.b1(self.c1(x)))
h = F.leaky_relu(self.b2(self.c2(h)))
return h
アップサンプルモジュールは以下のようになり、BN-Conv-BN-Activation, Conv-BN-Activation, Upsamplingのから構成されます。

Chainerで書くと以下になります。
def bilinear_upsampling(x):
_, _, height, width = x.shape
h = F.resize_images(x, (height*2, width*2))
return h
class UpsampleBlock(chainer.Chain):
def __init__(self, in_channel, out_channel, is_upsampling=True):
super(UpsampleBlock, self).__init__()
self.is_upsampling = is_upsampling
with self.init_scope():
self.b0 = L.BatchNormalization(in_channel)
self.c1 = L.Convolution2D(in_channel, out_channel, 3, pad=1)
self.b1 = L.BatchNormalization(out_channel)
self.c2 = L.Convolution2D(out_channel, out_channel, 3, pad=1)
self.b2 = L.BatchNormalization(out_channel)
def __call__(self, x):
h = self.b0(x)
h = F.leaky_relu(self.b1(self.c1(h)))
h = F.leaky_relu(self.b2(self.c2(h)))
if self.is_upsampling:
h = bilinear_upsampling(h)
return h
スキップモジュールは、Conv-BN-Activationというシンプルな構成です。
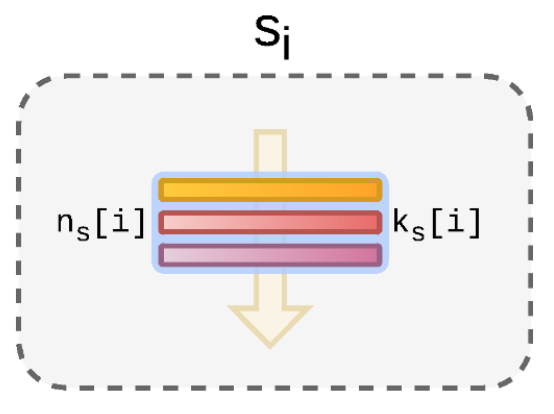
Chainerで書くと、以下のようになります。
class SkipBlock(chainer.Chain):
def __init__(self, in_channel, out_channel):
super(SkipBlock, self).__init__()
with self.init_scope():
self.c1 = L.Convolution2D(in_channel, out_channel, 3, pad=1)
self.b1 = L.BatchNormalization(out_channel)
def __call__(self, x):
h = F.leaky_relu(self.b1(self.c1(x)))
return h
さて、ネットワーク全体としては、以下のような構成になります。
class PriorNet(chainer.Chain):
def __init__(self, input_dim, latent_dim=128):
super(PriorNet, self).__init__()
with self.init_scope():
self.d1 = DownsampleBlock(input_dim, latent_dim)
self.d2 = DownsampleBlock(latent_dim, latent_dim)
self.d3 = DownsampleBlock(latent_dim, latent_dim)
self.d4 = DownsampleBlock(latent_dim, latent_dim)
self.d5 = DownsampleBlock(latent_dim, latent_dim)
self.s1 = SkipBlock(latent_dim, 4)
self.s2 = SkipBlock(latent_dim, 4)
self.s3 = SkipBlock(latent_dim, 4)
self.s4 = SkipBlock(latent_dim, 4)
self.u1 = UpsampleBlock(latent_dim + 4, latent_dim)
self.u2 = UpsampleBlock(latent_dim + 4, latent_dim)
self.u3 = UpsampleBlock(latent_dim + 4, latent_dim)
self.u4 = UpsampleBlock(latent_dim + 4, latent_dim)
self.u5 = UpsampleBlock(latent_dim, latent_dim, is_upsampling=False)
self.c0 = L.Convolution2D(latent_dim, 3, 1)
def __call__(self, x):
d1 = self.d1(x)
d2 = self.d2(d1)
d3 = self.d3(d2)
d4 = self.d4(d3)
d5 = self.d5(d4)
s1 = self.s1(d1)
s2 = self.s2(d2)
s3 = self.s3(d3)
s4 = self.s4(d4)
u5 = bilinear_upsampling(d5)
u4 = self.u1(F.concat((u5, s4)))
u3 = self.u2(F.concat((u4, s3)))
u2 = self.u3(F.concat((u3, s2)))
u1 = self.u4(F.concat((u2, s1)))
ret = self.u5(u1)
ret = F.sigmoid(self.c0(ret))
return ret
ロス関数
ロス関数は、単純に生成画像と元画像のMSEを取るだけです。
E(x;x_0) = ||x-x_0||^2
ただし、超解像をする場合は、
E(x;x_0) = ||D(x)-x_0||^2
と、目的の拡大後の生成画像$x$に対して、ダウンサンプルした$D(x)$によって評価します。また、インペインティングの場合は、
E(x;x_0) = ||(x-x_0) \odot m||^2
と、マスクされた領域$m$との要素積を取って、画像が存在する領域だけで評価するなど、ちょっとした変形を用います。
学習
Adamを使って、固定したノイズ$z$から所定の画像に変換するパラメータ$\theta$を学習しましょう。
for iter in tqdm.tqdm(range(1000)):
xp = model.xp
x_data = net_input.copy() + np.random.rand(1, input_dim, hh, hw).astype(np.float32) / 30
x = chainer.Variable(xp.asarray(x_data))
y = chainer.Variable(xp.asarray(img))
optimizer.update(model, x, y)
実験
さて、実験です。今回はこのAKBの画像を対象に色々やっていきましょう。誰が誰だか分かりますか?僕は3人くらい分かります(このページから拾ってきたけど、勝手に使って大丈夫だろうか・・・)。
Denoising
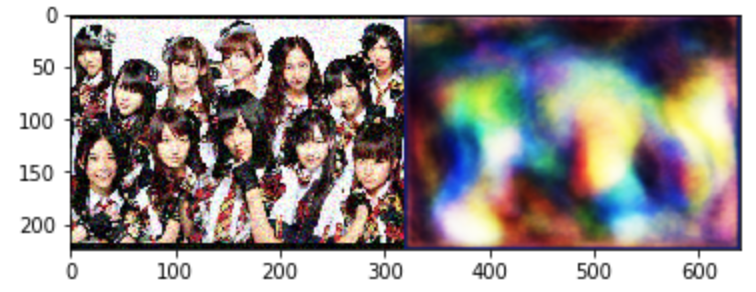
まずは、画像にガウシアンノイズを入れてみましょう。
ランダムノイズを入力して未学習のネットワークで出力すると以下の右のような模様が現れます。これが初期状態。完全にランダムな画像が出るのではなく、何となく規則性を持っているのが確認できます。これが、Convolutionが構造物を復元しやすい所以なのかもしれません。知らんけど。
で、1000回くらいパラメータを更新した結果がこちら。まぁまぁ綺麗になっていますね。とりあえず良しとしましょう。
JPEG Artifact
不可逆圧縮であるJPEG圧縮すると、アーティファクトが出るという問題があります。本手法はこのようなアーティファクトも消すことができます。まずは、先の画像にアーティファクトを乗せてやりましょう。背景や肌などの色が圴一の領域を中心として確かにアーティファクトが乗っている事が確認できます。
encode_param=[int(cv2.IMWRITE_JPEG_QUALITY),20]
result,encimg = cv2.imencode('.jpg', img, encode_param)
decimg=cv2.imdecode(encimg,1)
Image.fromarray(decimg)
これに対して、Deep Image Priorを掛けてみるとこんな感じになりました。アーティファクトは確か軽減されてはいますね。アヒル口も消えてしまっていますが、やはりニューラルネットワーク的にはアヒル口は不自然なのかもしれません。僕は好きなんですが。。
超解像
次は超解像をやってみましょう。先ほどの画像を縦横それぞれ1/4にするとこんな感じになります。
ちっさ。Bilinear補間で元に戻すとこんな感じになります。ボケてますね。正月明けの私のようです。本当にありがとうございました。
さて、これをDeep Image Priorで復元すると、以下のようになります。
・・・ちょっとマシ。元画像が小さすぎましたね。あまりインスタ映えしないので、元画像を大きくして再度チャレンジ。まずは、Bilinear補間画像はこうなります。
これをDeep Image Priorすると・・・。
惜しい感じ。折角なので、これに更にDenoisingを掛けた結果がこちら。
変わらない。
変わらない理由ですが、この画像に出てくるようなアーティファクトはConvolution特有のアーティファクトなのだと考えています。著者らはConvolutionだと自然画像の特徴が良い感じに出るぜ!と主張していますが、自然っぽさ以外にConvolution特有のアーティファクトも同時に出てしまうのが、現状なのだと思います。GANとかやってても、格子みたいな模様が出やすい的な。
Inpainting
最後は画像のInpaintingです。よく、体験版ソフトで画像を出力したら、思いっきり「Sample」とか出力画像に書かれていて腹が立つことがありますよね。それを消してやりましょう。取り敢えず、AKBの画像にモー娘。と書いてやりました。
さて、ちゃんとモー娘。からAKBになれるでしょうか。結果はこちら。
ちょーっとだけモー娘。が残ってますが、まぁAKBでしょう。めでたし。
終わりに
本当は、Convolutionのアーティファクトとか、結局何を学習できているのかとか、色々調査したいですが、もう2時なので、この辺で終わろうかと思います。