閲覧いただき、ありがとうございます。
pbirdyellowです。
今回はAAの出現回数を100万ハンドから推定してみました。
具体的には、今後プレーするであろう未知の2000ハンドに対して、AAがどれくらいの確率でどのくらい出現するのか推定します。
推定の手順は以下となります。
①ハンドを集計してヒストグラムを作成する
②集計したハンドに正規性があるかを検定する
③平均値、標準偏差値を求める
④AAの出現回数を精度95%で推定する
上記の内容や以降登場する専門用語については、下記の書籍がすごく分かりやすいので載せておきます。
・「完全独習 統計学入門 Kindle版」 小島 寛之 (著)
https://amzn.to/3mSPpqf
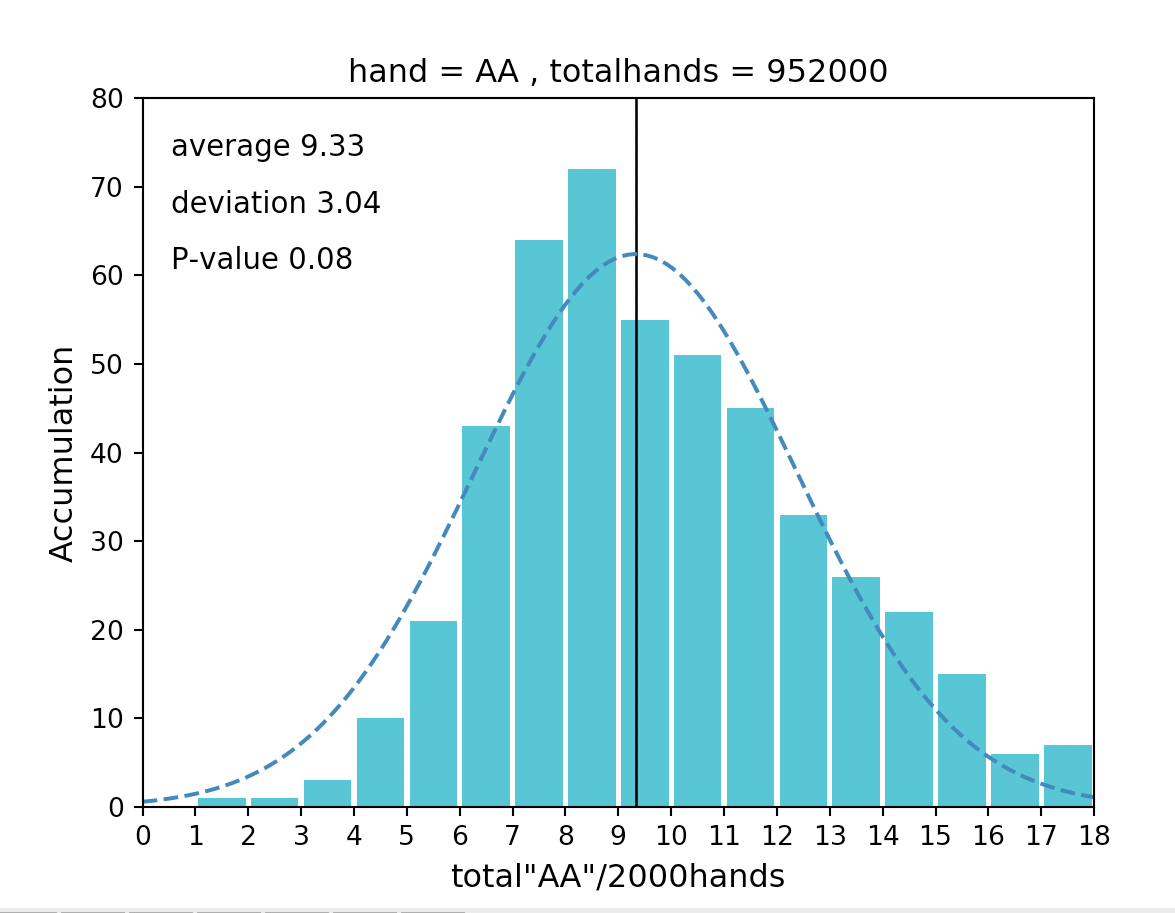
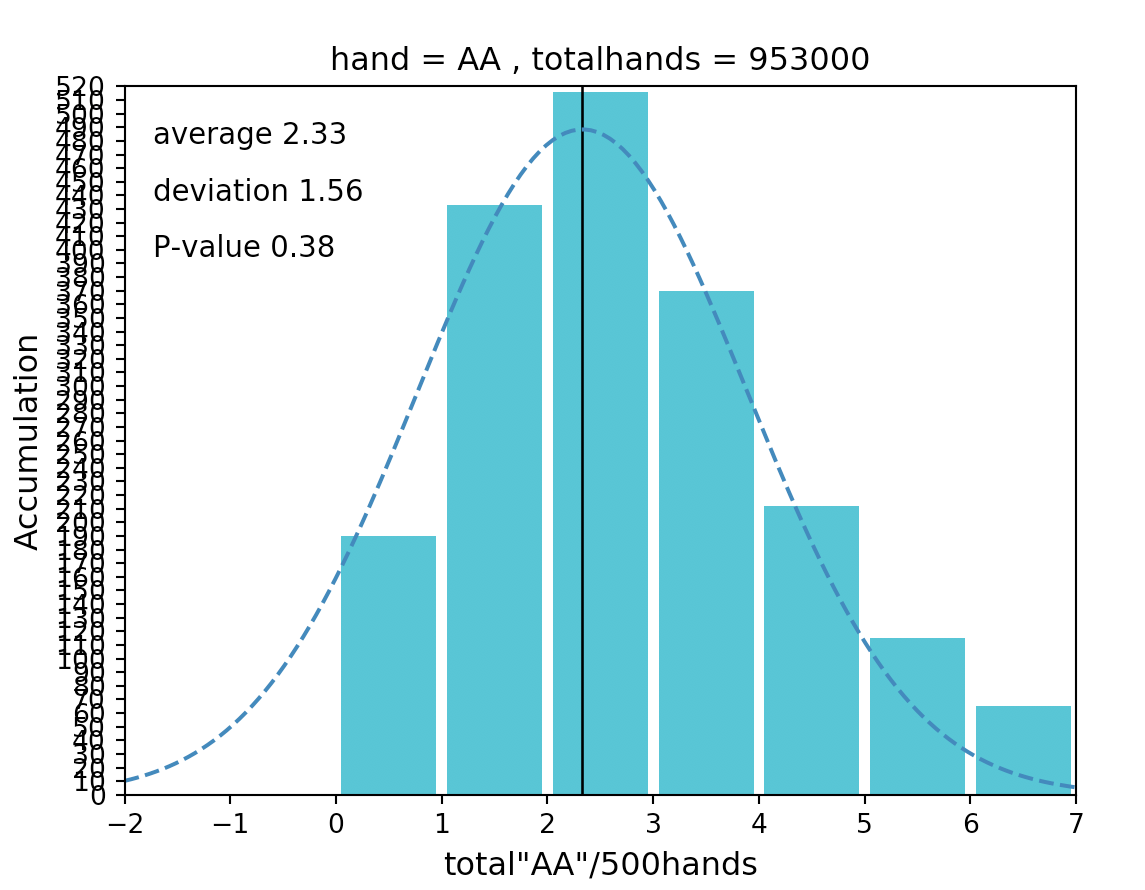
以下が結論をまとめたヒストグラムになります。
本記事のヒストグラムでは、縦軸は積算値、横軸は2000ハンドでAAが出現した回数を表しています。
■ヒストグラムとは
ヒストグラムとは、簡単に言うと「集計したデータを積み上げたグラフ」です。
上図を例にすると
・2000ハンド毎にAAが出現した回数が8回(横軸)であった事が、100万ハンドの中では72回(縦軸)あった
・2000ハンド毎にAAが出現した回数が2回(横軸)であった事が、100万ハンドの中では1回(縦軸)あった
などとなります。
■SW検定とは
正規性かどうかの検定方法は様々ありますが、今回はSW検定と言うものを使います。
SW検定とは集計したデータの、そもそものデータ群(=母集団)に正規性があるかを検証する手法です。
正規性があると様々な法則が使えます。そしてそれらの法則を用いてAAの出現回数を推定する事が可能です。
またSW検定ではp値を用いて正規性を判断します。
p値とは母集団に正規性があると仮定した場合、母集団からランダムにデータを選んで分布させた時、集計したデータのように分布する確率を表した値です。
一般的に、分布する確率が5%未満であった場合、それはあまりにも低すぎるので、そもそも母集団には正規性のもつ規則がない(=母集団には正規性がない)と判断されます。
上図ではp値(P-value)が0.08>0.05(=5%)なのでギリギリ正規性があると言えます。
■平均値と標準偏差値
上図の
・average→平均(μ)
・deviation→標準偏差(σ)
が該当します。
■精度95%の推定方法
集計したデータの平均値をμ、標準偏差値をσとすると
95%の確率で「μ-1.96σ≦x≦μ+1.96σ」内にAAの出現回数が収まります。
なので**「2000ハンドプレーするとAAは95%の確率で3.37回以上、15.29回以下の回数出現する」**
ことになります。
あくまで100万ハンドのデータを元に推定しているので上記の推定値には多少の誤差があります。
データが増え、平均値や標準偏差値が母平均値や母標準偏差値に近づくと推定値も正確な値となります。
※しかしこの数値は神のみぞ知る値になります
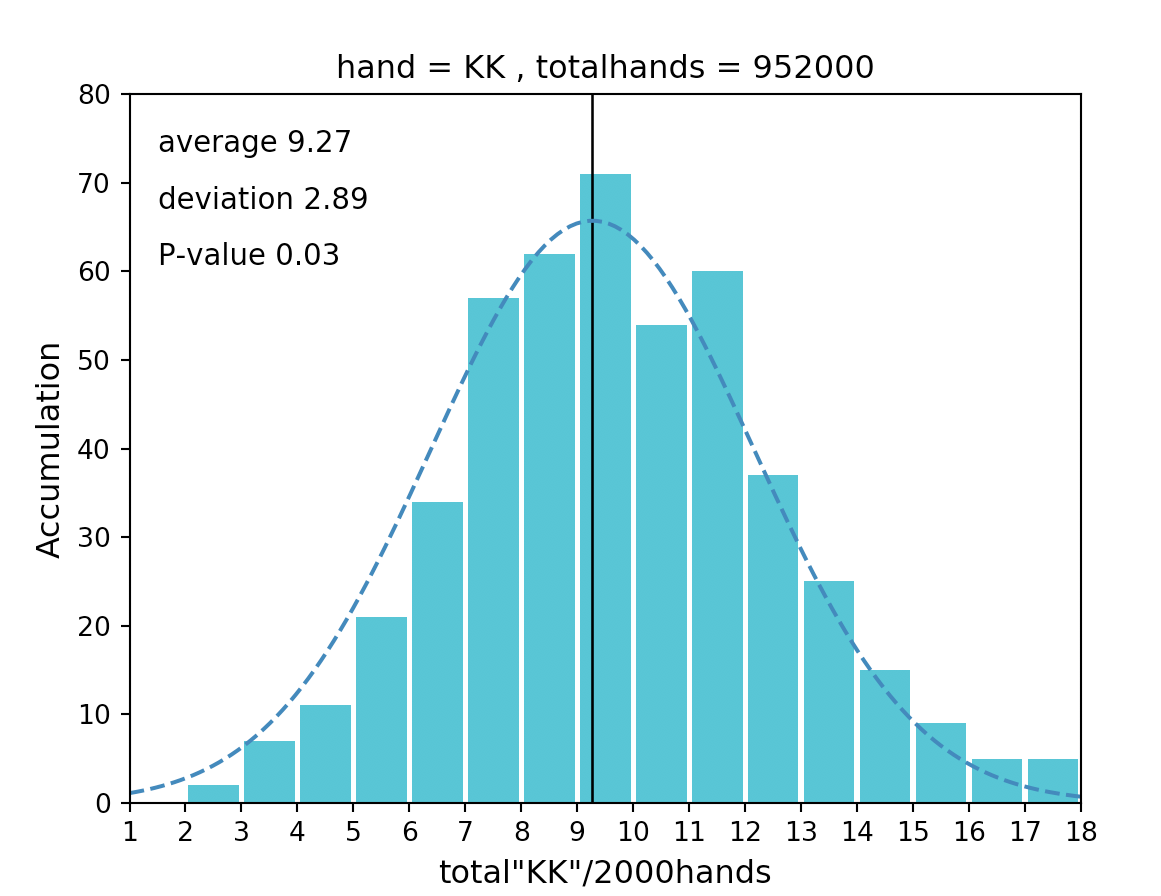
ちなみにKKの場合だと以下となります。
P-value=0.03<0.05 なので仮定が棄却されて母集団には正規性がないと言うことになります。
この場合、集計したデータにも正規性はないので精度95%の推定算出はできません。
しかし、ハンド数がもっと増えるとP-valueの値は大きくなり正規性があるデータになると思います。
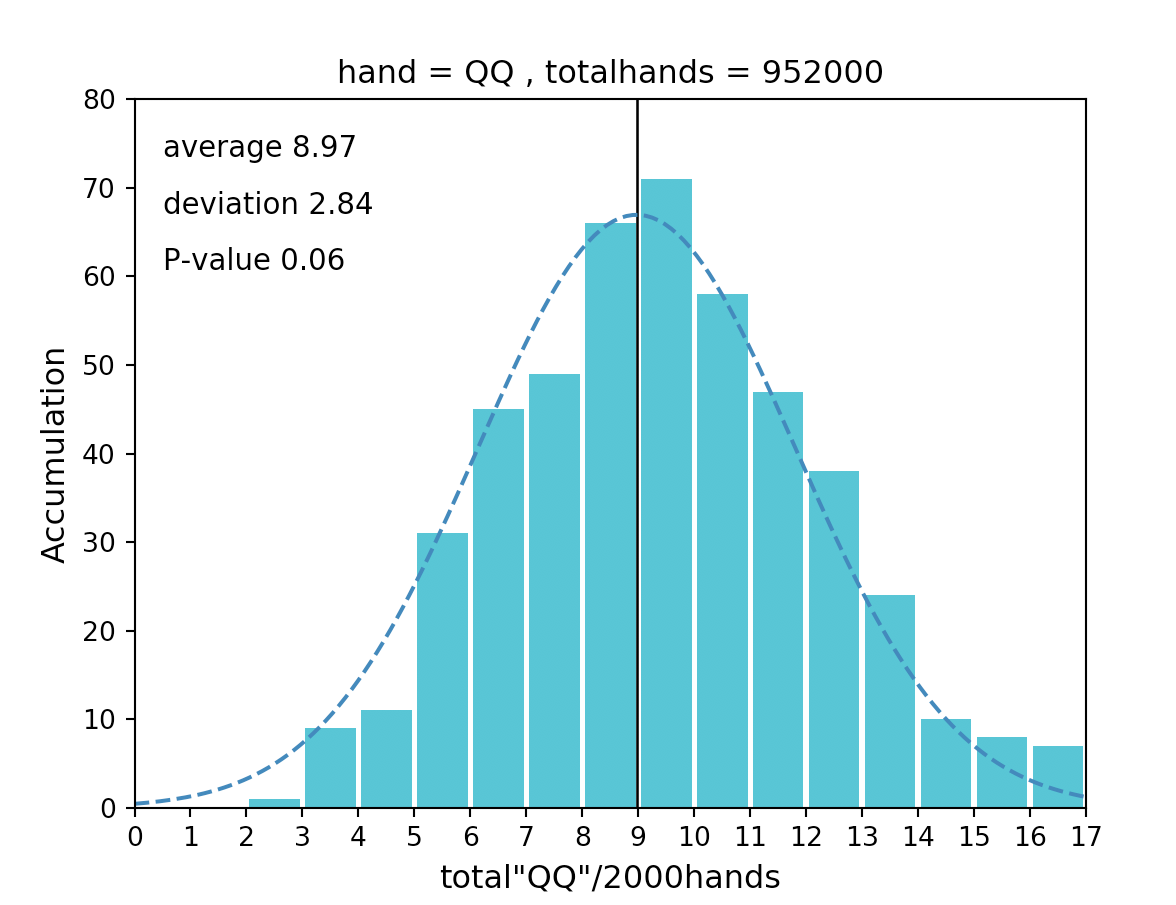
QQの場合だと正規性があり**「2000ハンドプレーするとQQは95%の確率で3.40回以上、14.54回以下の回数出現する」** となります。
ところで、なんでKKには正規性ないねん。AAとかQQのヒストグラムと何が違うんや!
と仰る方もいらっしゃると思います。
・・・仰るとおりです!!!
これはp値が境界ギリギリの数値周辺で推定しているのが悪いです。
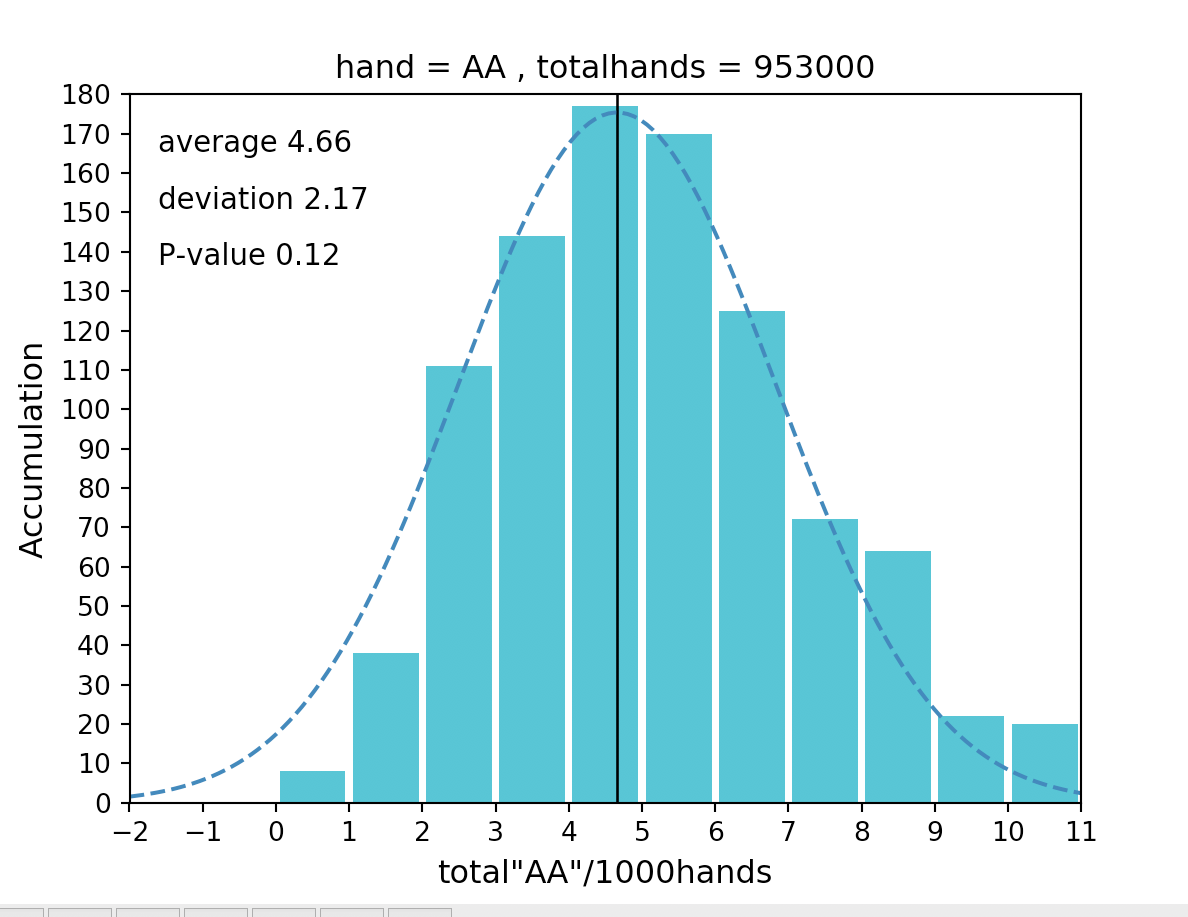
2000ハンドごとを1000ハンドごとに変えるなどすれば、この問題は解消されます。
しかしこれはこれで問題で、横軸の数値は0以上しかとらないので、きちんとした分析ができなくなってしまいます・・・
要は100万ハンドでは少なすぎるということです笑
とはいえこのような複雑な計算がPythonだと一瞬でできるので本当に便利です。
ソースコードを置いておくので、是非みなさまも活用してみてください!!
実のところ、SW検定の中身はあまりよく分かってないです。
Pythonではたった一行で計算できてしまうので、どういう数値が得られるのか分かっても計算過程は中々身につかないものです。
実例も交えて説明されている書籍等がありましたら、是非教えていただけると嬉しいです!
以下がソースコードになります。
プログラムは完全初心者なので、より良いコードの書き方等ありましたら是非ご指摘ください!!
from holdcards import Holdcards
from plotgraph import Plotgraph
import os
import glob
import re
path='ここにパスを記述'
hand = "AA" #調べたいハンドを記述
count = 2000 #調べたいハンド毎を記述
num = lambda val : int(re.sub("\\D", "", val))
filelist = sorted(glob.glob(os.path.join(path,"*.txt"),recursive=True),key = num)
totcards = []
graphdata = []
countdata = []
counthands = []
for item in filelist:
print(item)
with open(item) as f:
data = f.readlines()
card = Holdcards()
h_cards = card.find_holdcards(data)
totcards += h_cards
i = 0
while len(totcards[count*i:count*(i+1)]) == count:
graphdata.append(totcards[count*i:count*(i+1)])
i += 1
for item in graphdata:
countdata.append(item.count(hand))
graph= Plotgraph()
graph.writehist(countdata,hand,count,len(graphdata)*count) #SW検定-正規化
class Holdcards:
def __init__(self):
self.trump={"A":"14","K":"13","Q":"12","J":"11","T":"10","9":"9","8":"8","7":"7","6":"6","5":"5","4":"4","3":"3","2":"2"}
self.r_trump={"14":"A","13":"K","12":"Q","11":"J","10":"T","9":"9","8":"8","7":"7","6":"6","5":"5","4":"4","3":"3","2":"2"}
self.hands = 0
self.tothands = 0
self.handlist = []
def find_holdcards(self,data):
holdcards = []
for item in data:
if 'Dealt to' in item:
item = item[-7:-2]
if item[1] == item[4]:
if int(self.trump.get(item[0])) > int(self.trump.get(item[3])):
item = item[0] + item[3] + 's'
else:
item = item[3] + item[0] + 's'
else:
if int(self.trump.get(item[0])) > int(self.trump.get(item[3])):
item = item[0] + item[3] + 'o'
elif item[0] == item[3]:
item = item[0] + item[3]
else:
item = item[3] + item[0] + 'o'
holdcards.append(item)
return holdcards
import numpy as np
import pandas as pd
import scipy.stats as st
import math
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import matplotlib.transforms as ts
class Plotgraph:
def __init__(self):
pass
def writehist(self,countdata,hand,count,tothands):# 平均mu、標準偏差sig、正規乱数の個数n
df = pd.DataFrame( {'p1':countdata} )
target = 'p1' # データフレームのなかでプロット対象とする列
# (1) 統計処理
mu = round(df[target].mean(),2) # 平均
sig = round(df[target].std(ddof=0),2)# 標準偏差:ddof(自由度)=0
print(f'■ 平均:{df[target].mean():.2f}、標準偏差:{df[target].std(ddof=0):.2f}')
ci1, ci2 = (None, None)
# グラフ描画パラメータ
x_min = round(mu - 3*sig)
x_max = round(mu + 3*sig) # プロットする点数範囲(下限と上限)
j = 10 # Y軸(度数)刻み幅
k = 1 # 階級
bins = int((x_max - x_min)/k) # 区間の数 (x_max-x_min)/k (100-40)/5->12
d = 0.001
#ここから描画処理
plt.figure(dpi=96)
plt.xlim(x_min,x_max)
hist_data = plt.hist(df[target], bins=bins, color='tab:cyan', range=(x_min, x_max), rwidth=0.9)
n = len(hist_data[0]) # 標本の大きさ
plt.title("hand = "+hand+" , totalhands = "+str(tothands))
# (2) ヒストグラムの描画
plt.gca().set_xticks(np.arange(x_min,x_max-k+d, k))
# 正規性の検定(有意水準5%)
_, p = st.shapiro(hist_data[0])
print(hist_data[0])
print(st.shapiro(hist_data[0]))
if p >= 0.05 :
print(f' - p={p:.2f} ( p>=0.05 ) であり母集団には正規性があると言える')
U2 = df[target].var(ddof=1) # 母集団の分散推定値(不偏分散)
print(U2)
DF = n-1 # 自由度
SE = math.sqrt(U2/n) # 標準誤差
print(SE)
ci1,ci2 = st.t.interval( alpha=0.95, loc=mu, scale=SE, df=DF )
else:
print(f' ※ p={p:.2f} ( p<0.05 ) であり母集団には正規性があるとは言えない')
# (3) 正規分布を仮定した近似曲線
sig = df[target].std(ddof=1) # 不偏標準偏差:ddof(自由度)=1
nx = np.linspace(x_min, x_max+d, 150) # 150分割
ny = st.norm.pdf(nx,mu,sig) * k * len(df[target])
plt.plot( nx , ny, color='tab:blue', linewidth=1.5, linestyle='--')
# (4) X軸 目盛・ラベル設定
plt.xlabel('total"'+str(hand)+'"/'+str(count)+'hands',fontsize=12)
plt.gca().set_xticks(np.arange(x_min,x_max+d, k))
# (5) Y軸 目盛・ラベル設定
y_max = max(hist_data[0].max(), st.norm.pdf(mu,mu,sig) * k * len(df[target]))
y_max = int(((y_max//j)+1)*j) # 最大度数よりも大きい j の最小倍数
plt.ylim(0,y_max)
plt.gca().set_yticks( range(0,y_max+1,j) )
plt.ylabel('Accumulation',fontsize=12)
# (6) 平均点と標準偏差のテキスト出力
tx = 0.03 # 文字出力位置調整用
ty = 0.91 # 文字出力位置調整用
tt = 0.08 # 文字出力位置調整用
tp = dict( horizontalalignment='left',verticalalignment='bottom',
transform=plt.gca().transAxes, fontsize=11 )
plt.text( tx, ty, f'average {mu:.2f}', **tp)
plt.text( tx, ty-tt, f'deviation {sig:.2f}', **tp)
plt.text( tx, ty-tt-tt, f'P-value {p:.2f}', **tp)
plt.vlines( mu, 0, y_max, color='black', linewidth=1 )
plt.show()