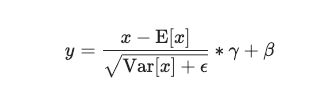Llama3のモデルを眺めていた際に、元のTransformerでLayerNormalization が使われていたところを RMS Normalization に置き換わっていることに気づいた。それらのPytorchでの実装がどのようになっているのかを確認したので備忘録として残す。ついでによく見るBatch Normalizationも確認する。
本記事の目的
- Batch, Layer, RMS Normalization の具体的な計算方法のNumpyによる確認
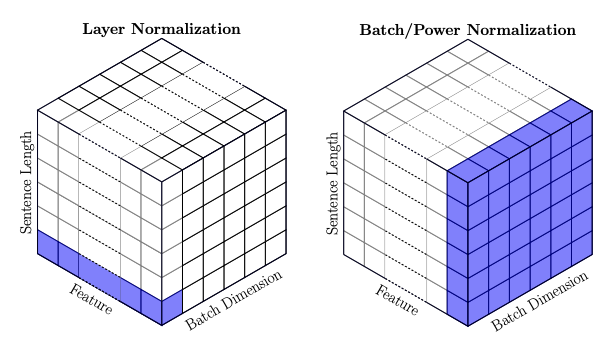
- 計算方法から保存される相対関係の軸とそうでない軸を特定
- 具体的な使用方法をみてどのような気持ちがあって使われているのかを推定(事実ではなく意見)
検証方法
ChatGPTを使用して以下のようにしてPytorch実装の中身を把握する。
- 適当なテンソルを作成
- Pytorch の forward メソッドで出力を得る
- Numpy 同様の Normalization の層を実装
- 上記の出力値が同じであることを確認し、Numpy の関数の眺め、具体的な処理を把握
入力のイメージと文字表記
今回は、3次元、4次元のテンソルを入力として考える。具体的なイメージがわかりやすいように以下のような具体例で話を進めていく。
- 3次元テンソル:$(N, L, C)$と表記し、BERT や GPT 等のNLPタスクを想像。(バッチサイズ, シーケンス長, トークンごとのチャネル数)で考える
- 4次元テンソル:$(N, C, H, W)$と表記し、VGG16 や ResNet 等の画像処理タスクを想像。(バッチサイズ, 高さ, 幅, チャネル数、)で考える
結論先出し
Normalization の目的はどれも学習の安定化であるが、保存できる相対関係と壊してしまう相対関係の軸が異なる。どの情報を残して起きたいかによって使い分ける必要がある。例えば、画像処理において、空間方向の相対関係を壊してしまうLayerNormalizationだけを使い続けるのは悪手となりうる。(他のNNの構造により役割分担するケースは考えられる)
| Batch Normalization | Layer Normalization | RMS Normalization | |
|---|---|---|---|
| 保存される相対関係 | トークン間(ピクセル間)とミニバッチ間の関係 | トークン(ピクセル)ごとのチャネル関係 | トークンごとのチャネル関係 |
| 破壊される相対関係 | トークン(ピクセル)ごとのチャネル関係 | トークン間(ピクセル間)の関係 | トークン間(ピクセル間)の関係 |
| 適している使用方法 | トークン(ピクセル間)の関係性を維持しつつ標準化 | チャネル間の関係性を維持しつつ標準化 | チャネル間の関係性を維持しつつ標準化 |
| 具体例 | ResNet50 | Transformer | Llama3 のTransformer |
Batch Normalization
まずはPytorchのBatchNorm1d、2d、から検証。なお、Pytorch に記載されている式は以下の通り。
BatchNorm1d
- 3次元以下のテンソル用の Batch Normalization のクラス
- Input : $(N,C)$ or $(N,C,L)$
- Output : $(N,C)$ or $(N,C,L)$
import torch
import numpy as np
# PytorchのBatchNorm1dの設定
batchnorm1d = torch.nn.BatchNorm1d(4, eps=1e-5, momentum=0.1, affine=False)
# 入力データ (2, 3, 4) - NumPy で生成し、PytorchのTensorに変換
x_np = np.random.randn(2, 3, 4).astype(np.float32)
x_torch = torch.tensor(x_np)
# PytorchでのBatchNorm1dの適用
# PytorchのBatchNorm1dは(Batch, Features, Length)の形式を期待するので、次元を変換する必要があります
x_torch_permuted = x_torch.permute(0, 2, 1) # (2, 4, 3) に変換
output_torch = batchnorm1d(x_torch_permuted)
output_torch = output_torch.permute(0, 2, 1) # 元の形状に戻す (2, 3, 4)
# NumPyでのBatchNorm1dの再現
def numpy_batch_norm(x, epsilon=1e-5):
mean = np.mean(x, axis=(0, 1), keepdims=True) # BatchとLengthに沿って平均を計算
var = np.var(x, axis=(0, 1), keepdims=True) # BatchとLengthに沿って分散を計算
normalized = (x - mean) / np.sqrt(var + epsilon) # 正規化
return normalized
# NumPyでの実装を適用
output_numpy = numpy_batch_norm(x_np)
# Pytorchでの出力とNumPyでの出力を比較
output_torch_np = output_torch.detach().numpy()
output_numpy, output_torch_np, np.allclose(output_numpy, output_torch_np, atol=1e-5)
これらの出力は一致する。注目すべきは、np.mean()でaxis=(0,1)と平均化の軸を指定しているということである。これはつまり、以下の処理を行うことである。
- $(N, L, C)$ → $(NL, C)$ に Reshape
- $\bar{c_i} = \sum_{n=1}^{NL}c_n$ として、チャネルごとに独立したC次元平均値ベクトルを算出
- 上記の平均値を使用してチャネルごとに独立したC次元平均値分散を算出
- チャネルごとに独立して平均が0、分散が1になるように標準化
つまり、バッチ方向、系列方向の相対関係は保存 され、チャネル方向の相対関係は破壊 される。NLPで言うと、単語間の相対関係と一緒に入力されるミニバッチ間の相対関係は保存されるということを意味している。
BatchNorm2d
- 4次元テンソル用の Batch Normalization のクラス
- Input : $(N,C, H, W)$ or $(N,C, H, W)$
- Output : $(N,C, H, W)$ or $(N, C, H, W)$
import torch
import numpy as np
# PytorchのBatchNorm2dの設定
batchnorm2d = torch.nn.BatchNorm2d(4, eps=1e-5, momentum=0.1, affine=False)
# 入力データ (2, 3, 3, 4) - NumPy で生成し、PytorchのTensorに変換
x_np = np.random.randn(2, 3, 3, 4).astype(np.float32)
x_torch = torch.tensor(x_np)
# PytorchでのBatchNorm2dの適用
# PytorchのBatchNorm2dは(Batch, Channels, Height, Width)の形式を期待するので、次元を変換する必要があります
x_torch_permuted = x_torch.permute(0, 3, 1, 2) # (2, 4, 3, 3) に変換
output_torch = batchnorm2d(x_torch_permuted)
output_torch = output_torch.permute(0, 2, 3, 1) # 元の形状に戻す (2, 3, 3, 4)
# NumPyでのBatchNorm2dの再現
def numpy_batch_norm2d(x, epsilon=1e-5):
mean = np.mean(x, axis=(0, 1, 2), keepdims=True) # BatchとHeightとWidthに沿って平均を計算
var = np.var(x, axis=(0, 1, 2), keepdims=True) # BatchとHeightとWidthに沿って分散を計算
normalized = (x - mean) / np.sqrt(var + epsilon) # 正規化
return normalized
# NumPyでの実装を適用
output_numpy = numpy_batch_norm2d(x_np)
# Pytorchでの出力とNumPyでの出力を比較
output_torch_np = output_torch.detach().numpy()
output_numpy, output_torch_np, np.allclose(output_numpy, output_torch_np, atol=1e-5)
これらの出力は一致する。注目すべきは、np.mean()でaxis=(0,1)と平均化の軸を指定しているということである。BatchNorm1dと同じことが言える。
- $(N, H, W, C)$ → $(NHW, C)$ に Reshape
- $\bar{c_i} = \sum_{n=1}^{NHW}c_n$ として、チャネルごとに独立したC次元平均値ベクトルを算出
- 上記の平均値を使用してチャネルごとに独立したC次元平均値分散を算出
- チャネルごとに独立して平均が0、分散が1になるように標準化
つまり、バッチ方向、画像の高さ方向、幅方向、相対関係は保存 され、チャネル方向の相対関係は破壊 される。CVで言うとピクセル同士の空間相対関係と、一緒に入力されるミニバッチ間の相対関係は保存されるということを意味している。
Layer Normalization
LayerNorm
- Layer Normalization を行うためのクラス。とりあえず一番最後の軸に沿って平均をとるので、何次元テンソルでも適用可能
- Input : (N, *)
- Output : (N, *)
import torch
import numpy as np
# PytorchのLayerNormの設定
layernorm = torch.nn.LayerNorm(4, eps=1e-5, elementwise_affine=False)
# 入力データ (2, 3, 4) - NumPy で生成し、PytorchのTensorに変換
x_np = np.random.randn(2, 3, 4).astype(np.float32)
x_torch = torch.tensor(x_np)
# PytorchでのLayerNormの適用
output_torch = layernorm(x_torch)
# NumPyでのLayerNormの再現
def numpy_layer_norm(x, epsilon=1e-5):
mean = np.mean(x, axis=-1, keepdims=True) # 特徴量に沿って平均を計算
var = np.var(x, axis=-1, keepdims=True) # 特徴量に沿って分散を計算
normalized = (x - mean) / np.sqrt(var + epsilon) # 正規化
return normalized
# NumPyでの実装を適用
output_numpy = numpy_layer_norm(x_np)
# Pytorchでの出力とNumPyでの出力を比較
output_torch_np = output_torch.detach().numpy()
output_numpy, output_torch_np, np.allclose(output_numpy, output_torch_np, atol=1e-5)
これらの出力は一致する。注目すべきは、np.mean()でaxis=-1と平均化の軸を指定しているということである。これはつまり、以下の処理を行うことである。
- $(N, L, C)$ → $(NL, C)$ に Reshape
- バッチ方向、シーケンス方向ごとに独立したNL次元平均値ベクトルを算出
- 上記の平均値を使用してチャネルごとに独立したNL次元平均値分散を算出
- バッチ、シーケンスごとに独立して平均が0、分散が1になるように標準化
つまり、トークンごとのチャネル方向の相対関係は保存 され、バッチ方向やシーケンス方向の相対関係 される。NLPで言うとトークンごとのチャネル方向の相対関係のみが保存されるということを意味している。
RMS Normalization
RMSNorm
- RMS Normalization を行うためのクラス。基本的な役割はLayerNormと同じだが計算量が7%から64%少ないというのが論文での主張
- Input : (N, *)
- Output : (N, *)
import torch
import numpy as np
# PyTorchのRMSNormのカスタム実装 (PytorchにはRMSNormがデフォルトではないため)
class RMSNorm(torch.nn.Module):
def __init__(self, dim, eps=1e-5):
super().__init__()
self.eps = eps
self.dim = dim
def forward(self, x):
rms = torch.sqrt(torch.mean(x ** 2, dim=-1, keepdim=True))
return x / (rms + self.eps)
# 入力データ (2, 3, 4) - NumPy で生成し、PytorchのTensorに変換
x_np = np.random.randn(2, 3, 4).astype(np.float32)
x_torch = torch.tensor(x_np)
# PyTorchでのRMSNormの適用
rmsnorm = RMSNorm(dim=4, eps=1e-5)
output_torch = rmsnorm(x_torch)
# NumPyでのRMSNormの再現
def numpy_rms_norm(x, epsilon=1e-5):
rms = np.sqrt(np.mean(x**2, axis=-1, keepdims=True)) # 特徴量に沿ってRMSを計算
normalized = x / (rms + epsilon) # 正規化
return normalized
# NumPyでの実装を適用
output_numpy = numpy_rms_norm(x_np)
# Pytorchでの出力とNumPyでの出力を比較
output_torch_np = output_torch.detach().numpy()
output_numpy, output_torch_np, np.allclose(output_numpy, output_torch_np, atol=1e-5)
これらの出力は一致する。注目すべきは、np.mean()でaxis=-1と平均化の軸を指定しているということである。これはつまり、以下の処理を行うことである。(Layer Norm と目的は大体一緒)
- $(N, L, C)$ → $(NL, C)$ に Reshape
- バッチ方向、シーケンス方向ごと独立したNL次元平均値ベクトルを2乗和によって算出
- 上記の2乗和で割る(分散を計算しなくて良いので計算量が抑えられる)
LayerNormと同様、トークンごとのチャネル方向の相対関係は保存 され、バッチ方向やシーケンス方向の相対関係 される。NLPで言うとトークンごとのチャネル方向の相対関係のみが保存されるということを意味している。
LayerNorm、RMSNormの気持ち
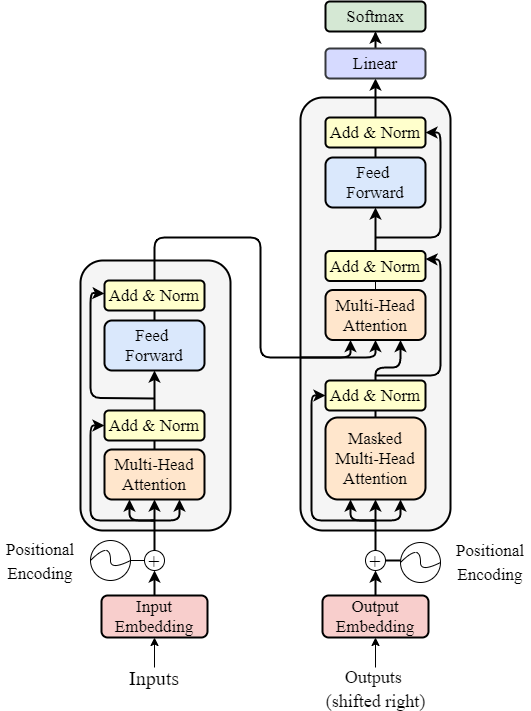
Transformerのアーキテクチャを観察して、LayerNormの気持ちを推測してみる。親の顔より見たであろうTransformer は以下の通り。
Encorder には2つの Add & Normが含まれており、それらの計算はそれぞれ以下のようになっている。
$$
h = \text{LayerNorm}(x + \text{Attention}(x))
$$
$$
\text{out} = \text{LayerNorm}(h + \text{FeedForward}(h_1))
$$
Attetion というのは、Multi-Head Self Attention を表しており、解説は他に譲る。FeedForwardも解説は他に譲るが、トークン間で独立に動く全結合層のように考えれば良い。Attention、FeedForward、LayerNorm には以下アルゴリズム的にの役割があると考えられる。
- Attention:トークン間の関係性に「注意」を向けつついい感じにトークンベクトルをミックスする
- LayerNorm:トークンごとの相対関係は(完全ではないだろうが)破壊され、トークンごとにチャネルの相対関係が保存される正規化をする
- FeedForward:トークンごとの相対関係を考慮せず、トークンごとにいい感じのベクトルに変換する
すなわち、Attenionの目的はトークン間の関係性を学習することで、FeedForward の目的は、チャネル間の関係性を学習することで、LayerNormの目的は、チャネル間の相対関係を維持しつつ、正規化することである。
このように考えると、なぜ、AttentionとFeedForwardの後にそれぞれスキップコネクションが入っているのかも何となくわかる気がする。(それぞれのブロックで学習できる情報と壊される情報をスキップコネクションの加算によって相互補完しているのでは?)
まとめ
結果の表を再掲します。
| Batch Normalization | Layer Normalization | RMS Normalization | |
|---|---|---|---|
| 保存される相対関係 | トークン間(ピクセル間)とミニバッチ間の関係 | トークン(ピクセル)ごとのチャネル関係 | トークンごとのチャネル関係 |
| 破壊される相対関係 | トークン(ピクセル)ごとのチャネル関係 | トークン間(ピクセル間)の関係 | トークン間(ピクセル間)の関係 |
| 適している使用方法 | トークン(ピクセル間)の関係性を維持しつつ標準化 | チャネル間の関係性を維持しつつ標準化 | チャネル間の関係性を維持しつつ標準化 |
| 具体例 | ResNet50 | Transformer | Llama3 のTransformer |
本記事では、3種類のNormalizationの具体的計算方法とその気持ちについて触れた。計算方法については、Python で実行すればNumpyが正しいことが確認できる。一方、気持ちの方は個人的な意見の域を出ていないので、補足訂正等があったらぜひ、コメントください。
参考資料