本記事の狙い
- ニューラルネットワークの記事などを読んでいると、全結合層や畳み込み層、損失関数といった「具体的な計算方法」に着目したものが多い
- 一方、論文や書籍を見ると、ニューラルネットワークを最適化数学の一部としてみて、抽象的な視点で語られていることが多い
- 本記事は、教師あり学習を最尤推定の視点から眺めるための、基礎をまとめたもの
何か間違いがありましたら、報告いただけると幸いです。
確率分布 (Probability Distribution)
以下の記事を参考にさせていただく。
確率変数(Random Variable)は、ある値を確率的に取る変数のことであり、確率変数が取る値とそのペアとなっる確率の対応の分布を確率分布(Probability Distribution)と呼ぶ。確率変数が連続値であるものを連続型確率分布、離散値であるものを離散確率分布と呼ぶ。今回は、各種確率分布を視覚化してわかりやすく理解することを目的としているので、離散確率分布で内容を記載する。
同時確率分布(Joint probability distribution)
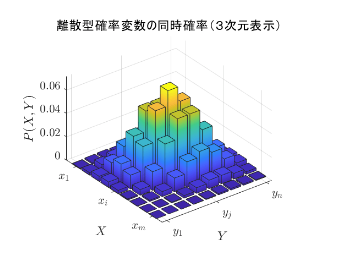
2つの確率変数を持つ確率分布である。2つの確率変数を$x_i, y_j$とすると、$x_i, y_j$の1組み合わせごとに、確率値が割り当てられている。以下の式を満たす。
$$P(x_i, y_j) >0 $$
$$ \sum_{i=1}^{m}\sum_{i=1}^{n}P(x_i, y_j) = 1$$
これは、確率分布の定義である。これを3次元に描画すると以下のようになる。高さが各$x_i, y_j$ペアの確率値を示す。
周辺確率分布(Marginal probability distribution)
同時確率分布$P(X,Y)$の一方の確率分布に着目し、その総和によって定義される確率分布を周辺確率という。
$$\sum_{j=1}^nP(x_i,y_j) = P(X=x_i) $$
$$\sum_{i=1}^nP(x_i,y_j) = P(Y=x_j) $$
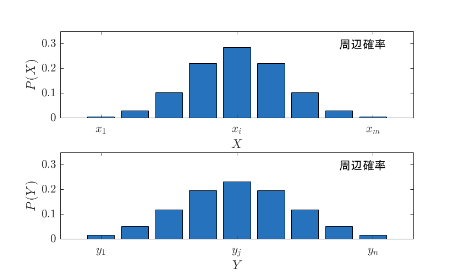
2変数の確率分布のうち一つの確率分布について周辺化すると1変数の確率分布となる。これは次元数が増えても同じである。先ほどの同時確率分布を周辺化した、周辺確率分布を視覚化すると以下のようになる。
周辺化はブルドーザーのイメージである。周辺化で消える確率変数の方向にブルドーザーを走らせ、そこにある砂の山(確率値)を積み上げていき、一つ次元が減った山が出来上がる。この周辺確率分布の上の図は、先ほど示した同時確率分布の y 軸方向にブルドーザーを走らせた結果である。
周辺化したとしても、砂全体の量(=確率値)は変化しないので、周辺化という計算プロセスの後、補正を加えなくても確率分布の条件を満たす。
条件付き確率分布(Conditonal probability distribution)
条件付き確率分布は、以下のように定義される。
$$P(X|Y=y_j) = \frac{P(X, Y=y_i)}{P(Y=y_i)} = \frac{P(X, Y=y_i)}{\sum_{i=1}^nP(x_i,y_j)}$$
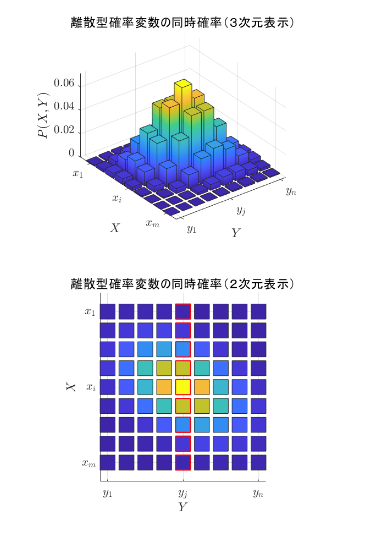
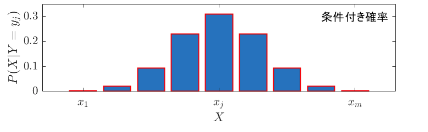
同時確率分布$P(x_i,y_j)$の一方の確率変数が特定の値となった分布を考えるのが条件付き確率分布である。先ほど示した同時確率分布を上から見ると、以下のようになる。
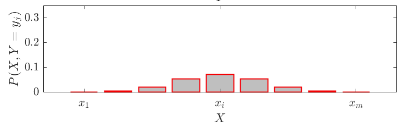
上図の下の上から分布を見た2次元表示図形のうち、赤い枠線の部分に注目する。つまり、$Y=y_j$に条件を固定して考える。この部分に何の変更を加えずに図示すると、以下のように、すべての確率を足し合わせても合計値が1を下回ってしまう。式で言うと $P(X, Y=y_i)$ に該当する。
これでは、確率の条件を満たさない。したがって、$\sum_{i=1}^nP(x_i,y_j)$を割ることで正規化してあげることで、確率分布となる。これが条件付き確率分布の定義である。
条件付き確率分布は、2次元の同時確率分布の1軸に注目し、1ラインずつを新たな確率分布とするものである。確率分布とするために、周辺化した値で割っているので、先ほどのブルドーザーの例を当てはめると、全体の砂の量は増えているということになる。
確率分布まとめ
- 同時確率分布$P(X,Y)$:複数の確率変数の組み合わせごとに確率値が割り当てられている分布
- 周辺確率分布$P(X)=\sum_{j=1}^{n}P(X, Y=y_i)$:周辺化により消去する確率変数の軸の方向に確率値を足し合わせていってできる分布
- 条件付き確率分布$P(X|Y=y_j)$:多次元確率分布において、確率を観測するラインを固定し、そのライン上の確率値の合計が1になるように正規化した確率分布
- $m$通りの値を取る離散確率変数 $X$と$n$通りの値をとる離散確率変数 $Y$からなる同時確率分布があった際、そこから得られる同時確率分布は$P(X|Y=y_j)$n通りとなる。つまり、上図で言うと、ライン1本1本が確率分布となる
- つまり、$p(a,b|c,d,...,z)$など、いくつか条件づけられている場合、基本的にはすべての同時確率分布を考えるが、条件付けられている$c,d,...,z$の軸方向に対しては正規化が適用されているような確率分布を想像すれば良い。
KLダイバージェンス
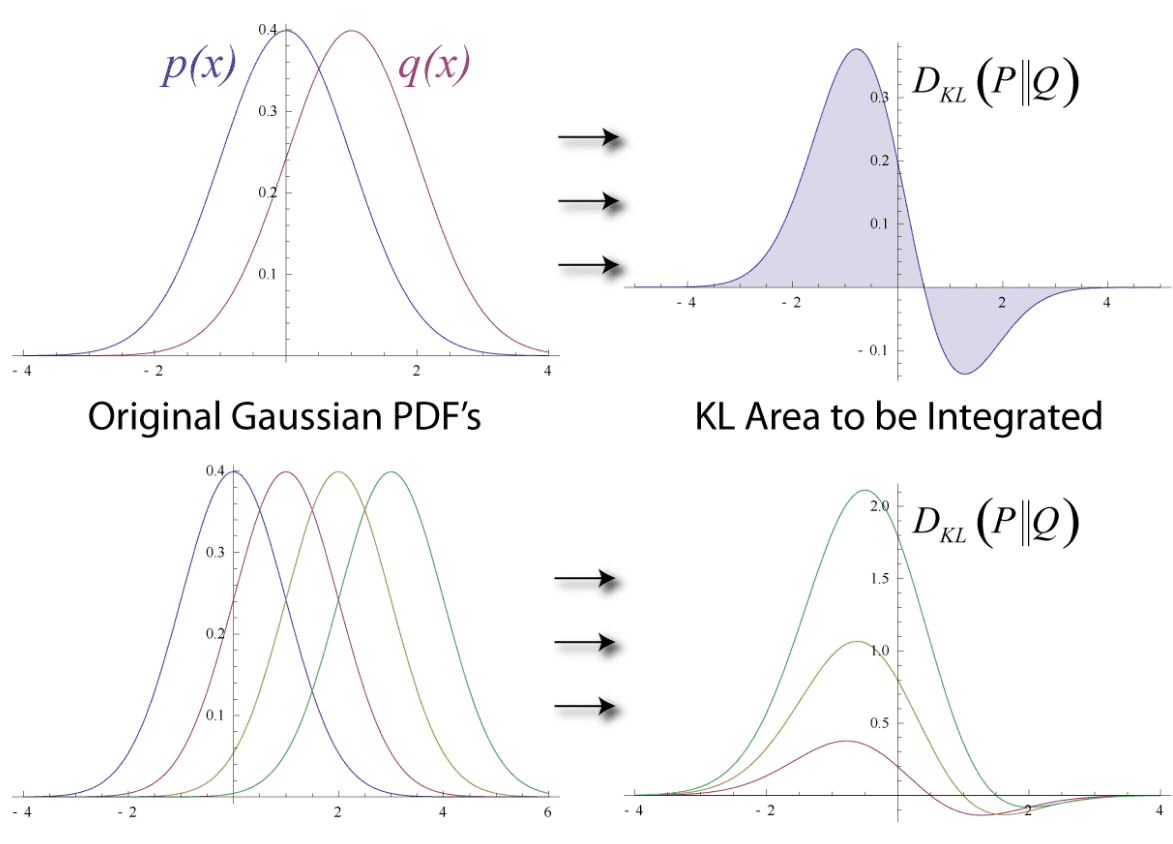
KLダイバージェンスとは、2つの確率分布の「近さ」を図る指標である。KLダイバージェンスが大きければ大きいほど、2つの確率分布は近いということが言える。
確率分布 $p$ と $q$ がある際、KLダイバージェンスは以下のように定義される。
$$D_{KL}(p||q) = \sum_{x}p(x)\text{log}\frac{p(x)}{q(x)}$$
また、KLダイバージェンスを以下のように変形すると、下式第二項にクロスエントロピーが出現する。
$$D_{KL}(p||q) = \sum_{x}p(x)\text{log}\frac{p(x)}{q(x)} = \sum_{x}p(x)\text{log}p(x) + \sum_{x}p(x)\text{log}q(x)$$
教師あり学習の例で考えてみる。 $p$を再現したい真の分布、$q$をモデルによる確率分布とすると、$q$を変えることによって、KLダイバージェンスを小さくするには、第二項のクロスエントロピーを小さくする必要があることがわかる。つまり、ニューラルネットワークの分類問題においてクロスエントロピーロスが使用されているのは、クロスエントロピーを小さくし、KLダイバージェンスを小さくすることで、モデル $q$ の確率分布を真の確率分布に近づけるという狙いがあると言うことである。
最尤推定(Most Likelihood Estimation)
最尤推定について記述する前に、尤度(Likelihood)と確率、確率密度(Probability density)の違いについて整理する。同時確率分布 $p(x,\theta)$ を想定する。これを尤度と考えた時と、確率密度で考えた時の違いについて説明する。
-
確率、確率密度(Probability density)
$p(x,\theta)$を確率もしくは確率密度としてみた場合、これはただ単に $x, \theta$ を2つの確率変数とみなし、それらの同時確率を考えているということになる。 -
尤度(Likelihood)
$p(x,\theta)$を尤度としてみた場合、一般に$x$は観測データを表し、$theta$はモデルのパラメータを表す。$x$は、観測データであるため、すでに得られているものと考え、$p(x,\theta)$を$\theta$の関数として捉える。
最尤推定は、尤度を最大化するパラメータを推定する手法であり、尤度とはある観測データ $x_1, x_2,...,x_n$が得られている際の各パラメータのもっともらしさのことである。つまり、最尤推定は、現在手元にあるデータが得られる確率が最も高いパラメータを推定する方法である。
モンテカルロ法(Monte Carlo Method)
モンテカルロ法とは、「確率変数のサンプリングをコンピュータを用いて乱数で行い、数値計算やシミュレーションを行う手法」である。本記事では、モンテカルロ法をKLダイバージェンスの最大化と尤度の最大化を結びつけるための手段としてまとめる。モンテカルロ法による近似の一般的な式を以下に記載する。
$$\text{E}_{p*(x)}[f(x)] = \int p*(x) f(x) dx \approx \frac{1}{N} \sum_{i=1}^Nf(x^{(i)}), x^{(i)}\sim p*(x)$$
$p*(x)$を確率分布、$f(x)$を任意の関数、$x^{(i)}$は、確率分布$p*(x)$からサンプリングされた全部で$N$個のデータのうちの一つを表している。つまり、モンテカルロ法を使用すると任意の関数の期待値をサンプリングしたデータを用いた計算の平均値で再現できると言うことである。
以下のシチュエーションを想定する。
- 確率変数:$x$
- モデルにより近づけたい真の確率分布:$q(x)$
- モデルによる確率分布($\theta$はモデルのパラメータ):$p(x;\theta)$
先ほど、説明した、KLダイバージェンスの定義式を変換していく。
\begin{align}
D_{KL}(q(x)||p(x;\theta)) & = \sum_{x}q(x)\text{log}\frac{q(x)}{p(x;\theta)}\\
& = \text{E}_{q(x)}[\text{log}\frac{q(x)}{p(x;\theta)}]\\
& \approx \frac{1}{N}\sum_{i=1}^N\text{log}\frac{q(x^{(i)})}{p(x^{(i)};\theta)}\\
& = \frac{1}{N}\sum_{i=1}^N\{\text{log}q(x^{(i)}) + \text{log}p(x^{(i)};\theta) \}
\end{align}
最後の式における、$\frac{1}{N}\sum_{i=1}^N \text{log}p(x^{(i)};\theta)$は、対数尤度関数になっているため、KLダイバージェンスとモデルの対数尤度には以下の関係がある。
$$
\text{argmax}_{\theta}\frac{1}{N}\sum_{i=1}^N \text{log}p(x^{(i)};\theta) =
\text{argmin}_{\theta}D_{KL}(q(x)||p(x;\theta))
$$
つまり、最尤推定で手持ちにデータにもっともフィットするパラメータ$\theta$を得るためには、対数尤度関数$\frac{1}{N}\sum_{i=1}^N \text{log}p(x^{(i)};\theta)$を最大化するパラメータを選べばよく、ひいては、真の分布(教師データ)とモデルの分布のKLダイバージェンスを最小化すれば良い。もっと言うとクロスエントロピーロスを最小化すれば良い。
モンテカルロ法は、KLダイバージェンスと対数尤度関数を理論的に結びつける役割を果たしている。
教師あり画像分類モデルに関して言うとまとめると以下の通り。
クロスエントロピーを小さくする = KLダイバージェンスを小さくする = 尤度を大きくする
教師あり分類問題を最尤推定の視点で見る
これまでの内容を理解すると、教師あり分類問題を最尤推定の視点で眺めることができる代表タスクとして画像分類を取り上げる。$M$個の学習用画像とそのラベル、$N$個のテスト用画像があることを想定する。。文字を以下のように定義する。
- $x_{train}^{(i)}, x_{test}^{(j)}$:学習入力データとテスト入力データ(分類したい画像$(i)$), $i=1,2,...,M$, $j=1,2,...,N$
- $t^{(i)}$:学習データの正解ラベル
- $y^{(j)}$:推論時のテスト入力データ $x_{test}^{(j)}$に対する出力
- $\theta$:モデルのパラメータ(NNにおける重みを想定)
教師あり画像分類タスクにおける対数尤度$L(\theta)$は以下のように定義される。
$$ L(\theta) = \sum_{i=1}^{M} \text{log} p(t^{(i)}|x_{train}^{(i)};\theta)$$
この式について説明する。$p$は、モデルによる確率分布を表している。また、対数尤度関数であるため、$x_{train}^{(i)}, t^{(i)}$は既知の値とみなし、$\theta$の関数であるとみる。なぜ同時確率分布$p(t^{(i)},x_{train}^{(i)})$ではなく、条件付き確率分布を使用しているかというと、我々が教師あり学習で獲得したい分類値は、画像値に正規化された分布だからである。
例えば、犬猫分類モデルを作成する際に、画像ごとに犬率0.7、猫率0.3などのように正規化されていた方がわかりやすい。
尤度を最大化する $\theta$ を求めるために、先ほど行ったようにKLダイバージェンスを絡めて以下のように考える。
\begin{align}
\text{argmax}_{\theta}\frac{1}{M}\sum_{i=1}^M \text{log}p(t^{(i)}|x^{(i)};\theta)
& =\text{argmin}_{\theta}D_{KL}(q(t|x)||p(t|x;\theta)) \\
& = \text{argmin}_{\theta} \sum_{x}q(x)\text{log}p(x;\theta)
\end{align}
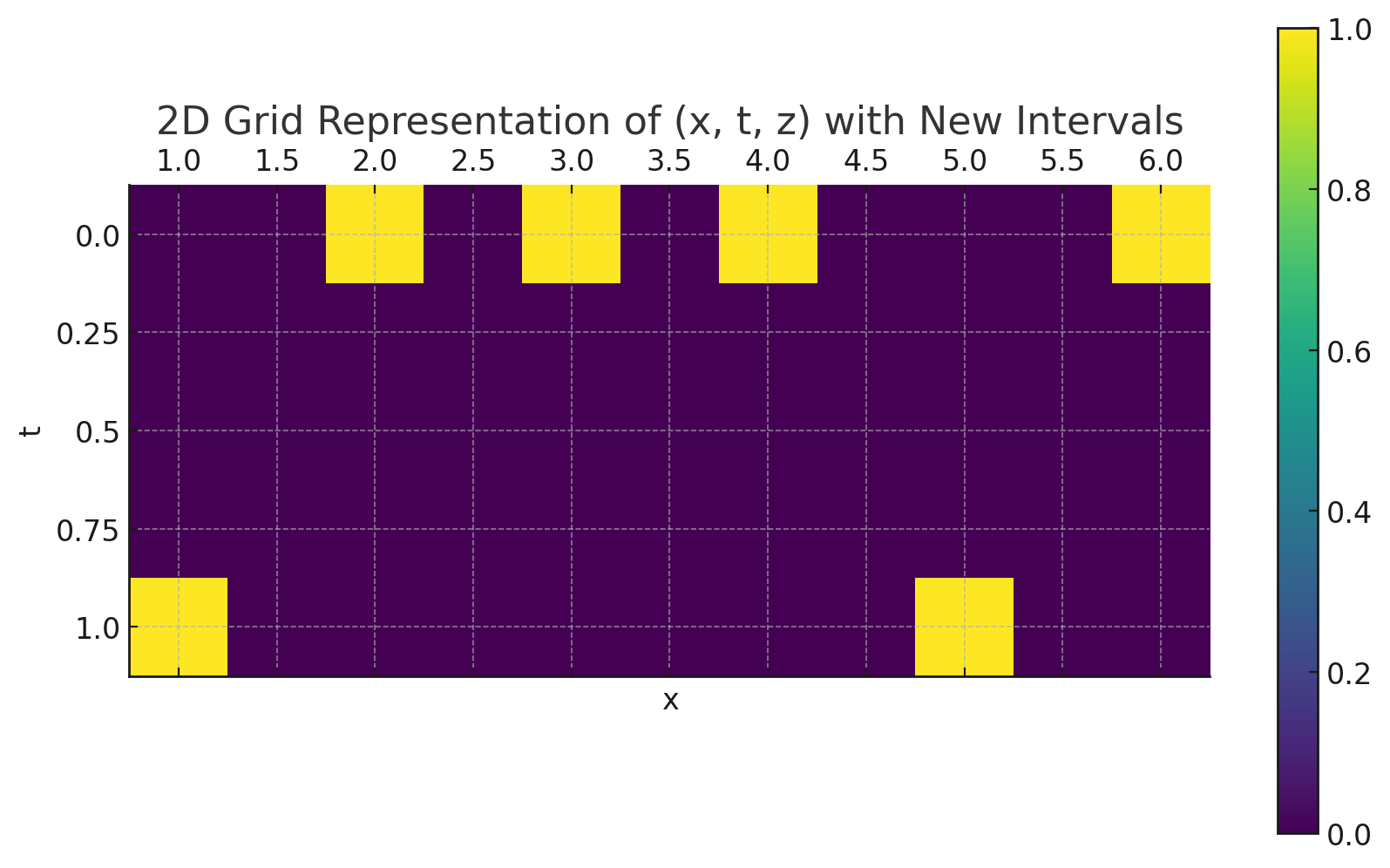
1段目の式変形は、対数尤度 → KLダイバージェンスの変形である。$q(t|x)$は、真の分布であるため、画像ごとの教師ラベルを表す。画像$x$を簡単のため、1次元で表し、2クラス分類として考え、図示すると$q(t|x)$は、以下のように考えることができる。(条件付き確率分布$q(t|x)$なので、$x$の値ごとにt軸方向に足し合わせると合計値がちゃんと1になる。
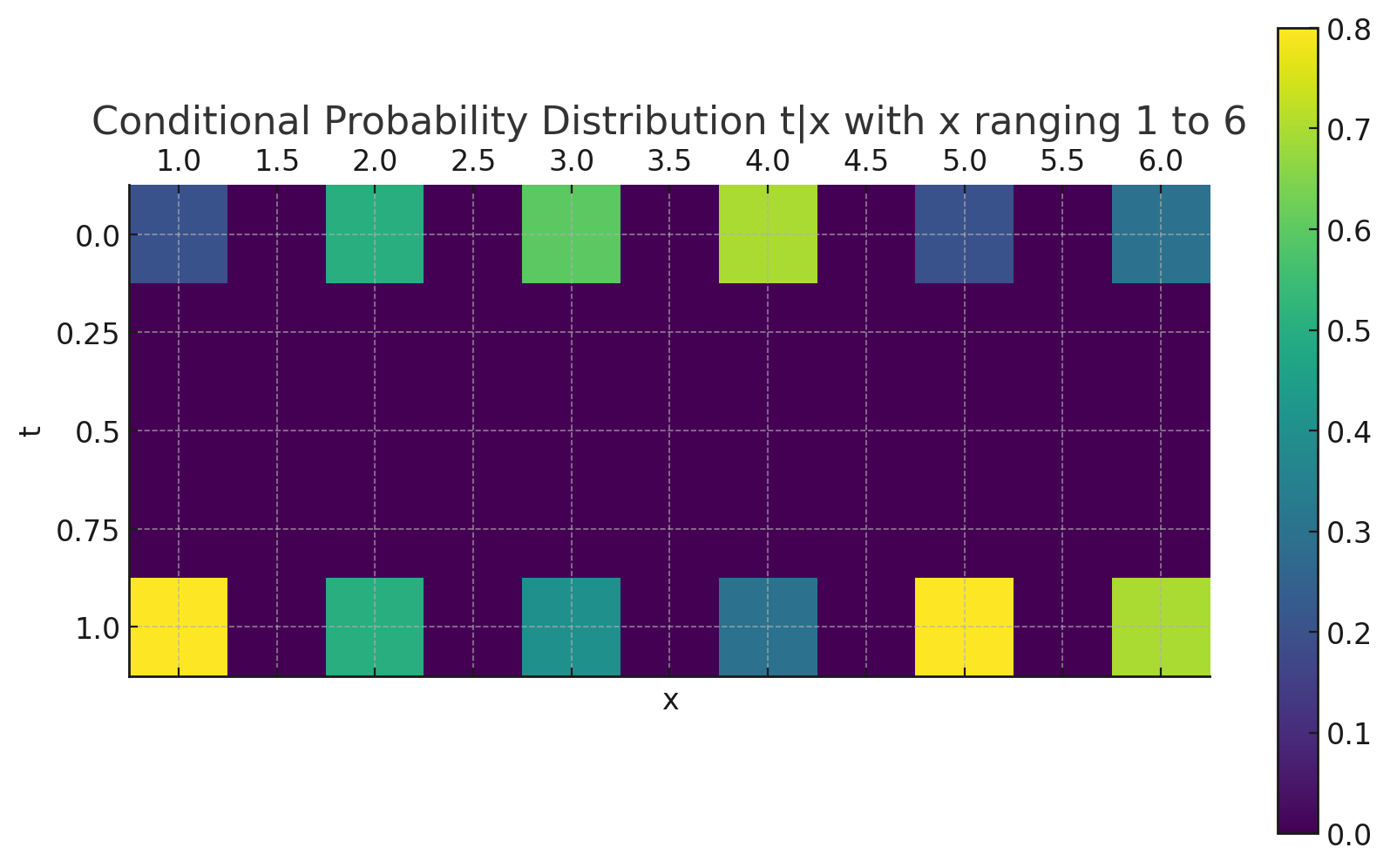
例えば、学習前のモデルの条件付き確率分布 $p(t|x;\theta))$ は以下のようになっているとする。以下の分布をパラメータ$\theta$を動かして、上の真の分布に近づける作業が分類問題における学習である。
KLダイバージェンスを最小化すれば、$p(t|x;\theta))$は$q(t|x)$に近づいていく。しかし、KLダイバージェンスの中でもパラメータ$\theta$に関係するのは、クロスエントロピー部分だけなので、そこだけを損失関数として使用すればよい。(変形2段目)
まとめ
- 対数尤度を大きくする = KLダイバージェンスを小さくする = クロスエントロピーを小さくする
- 上記の関係性は、モンテカルロ法によって接続される
- 教師あり学習のモデルは入力が観測された元での条件付き確率で表される。なぜならば、画像ごとに確率分布(非負かつすべてのクラスの確率を足し合わせたら1になる)を出力するから
参考サイト、文献
以下のサイト、書籍を参考にさせていただきました。
- Understanding Maximum Likelihood Estimation in Supervised Learning
https://theaisummer.com/mle/#binary-cross-entropy-bce-loss - 確率分布について
https://kesco.co.jp/%E7%A2%BA%E7%8E%87%E5%88%86%E5%B8%83/ - ゼロから作るDeep Learning5、生成モデル篇