「計算」を定義する

はじめに、「計算」について改めて考えてみたいと思います。
ここでは、自然数の足し算、掛け算について考えたいと思います。
ぱっと思い浮かぶ式にはどんな物があるでしょうか。
たとえば、
$$
1+1=2
$$

あるいは、

$$
2×3+4=10
$$

これらの計算を行うために必要なものを整理していきましょう。

まず大前提として、使うことができる記号を定義しないと始まらないです。

数字
- 0 - 9
計算記号
- +
- ×
- =

また、いま定義した記号に対して、どのような操作を行うかのルールを定めなければいけません。
「1+1=」という記号列が入力されたとして、ルールも何もない状態だと「2」という出力を得ることは不可能です。
自然数に関する数学的な扱いについては、きちんと公理としてまとめられています。
これをペアノの公理といいます。
Wikipediaから引用しますが、以下のようなものです。

0は自然数である。
任意の自然数 a にはその後者 (successor)、suc(a) が存在する（suc(a) は a + 1 の "意味"）。
0 はいかなる自然数の後者でもない（0 より前の自然数は存在しない）。
異なる自然数は異なる後者を持つ：a ≠ b のとき suc(a) ≠ suc(b) となる。
0 がある性質を満たし、a がある性質を満たせばその後者 suc(a) もその性質を満たすとき、すべての自然数はその性質を満たす。

例えば、「1+1=」という記号列にペアノの公理を適用すると、

公理2より、
$$1+1=\rm{suc} (1)=2$$

が得られます。ここで、$\rm{suc} (1)$のことを2と定義していることに注意です。

詳細は省きますが、上述の公理を組み合わせることで乗算に関する定理も導くことができ、「2×3+4=10」なんかも言うことができます。

まとめると、「自然数の計算」とは、

記号
- 0-9
- ×
- +
- =
ペアノの公理

からなり、記号列を入力とし、ペアノの公理を適用することにより出力を得る操作であると言えます。

ざっくり見てきましたが、自然数に限らず、一般的に「計算」と言われているものについて、もっと抽象的に考えられそうな気がしてきました。
以後、もっと深く議論するために、本記事では「計算」を以下の性質を持つものとして定義します。

有限の記号列を入力とする
記号列に関する操作規則が定義されている

用語整理

これから「計算」について考えていきたいのですが、その前に用語の定義だけちゃんとしておきたいと思います。

アルファベット
- 有限種類の記号からなる集合
系列
- いくつかのアルファベットの要素を連ねた記号列
言語
- 一定の規則によって生成されうる可能な系列の集合
空系列
- 何も文字がない系列
  - $\epsilon$で表す
計算機
- 予め定義されたアルファベット、記号操作規則により、入力系列から出力系列を得ることが可能な仮想的な機械

有限オートマトン

はじめに、簡単な計算機として有限オートマトンについて考えたいと思います。
有限オートマトンは、いくつかの内部状態を持った計算機です。
入力系列を受け取ると、開始状態から始まって、内部状態が遷移していきます。状態遷移が終わった段階で、内部状態がある特別な状態であるならば、入力系列を受理するというものです。
有限オートマトンは状態を○、状態遷移を→で表すと視覚的に理解しやすいです。
例えば、aとbだけからなる系列を入力とする場合を考えます。
この時、「aを偶数個含む文字列を受理する」有限オートマトンは、このように描けます。

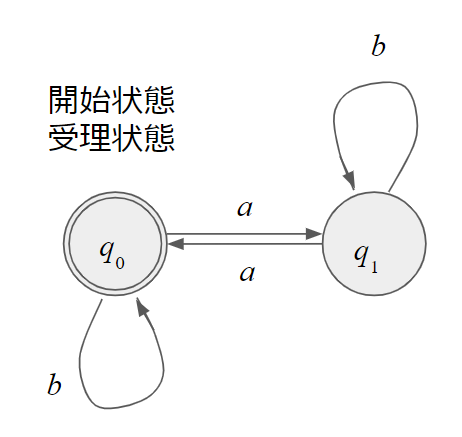
この有限オートマトンに「aab」という系列を入力した場合、系列の一番目の記号から順番に処理され、状態が遷移します。$q_0 \rightarrow q_0 \rightarrow q_1 \rightarrow q_0 \rightarrow q_0 $という内部状態の遷移を経て、最終的に受理状態である$q_0$で落ち着きます。

このように入力系列に対して計算を行い、受理するかどうかを判定するのが、有限オートマトンのやっている仕事です。

有限オートマトンは、以下の5項$(Q, \Sigma, \delta, q_0, F)$により、形式的に定義されます。

$Q$は状態の有限集合
$\Sigma$は有限のアルファベット(ただし空系列を含まない)
$\delta:Q×\Sigma\rightarrow Q$は状態遷移関数
$q_0 \in Q$は開始状態
$F \subseteq Q $は受理状態の集合

矢印と内部状態の組み合わせはいかようにも複雑になりえますが、この有限オートマトンの計算能力には限界があります。

結論から言うと、有限オートマトンが受理できるのは、以下の規則によって生成された記号列に限られます。

$a+b$
- 系列$a$または$b$を有限個連ねてできる可能な系列の集合
$a・b$
- 系列$ab$からなる集合
$a^*$
- 系列$a$を有限個(0個も可)連ねてできる可能な系列の集合

これらの規則から生成されうる系列の集合を、正規言語と言います。
先程の「aを偶数個含む系列」も、正規表現で書くことが可能です。

ある言語$L$が正規言語である時、その言語から生成される任意の系列を受理する有限オートマトンが少なくとも1つ存在します。
逆に、入力系列が正規言語に属さない場合、その系列を受理しうる有限オートマトンは存在しません。

正規表現でない例として、「正しいカッコの系列」があります。要は「()」とか「(()())」といった、カッコが正しく閉じている系列です。

証明の詳細は省きますが、(と)のみからなる系列を受け取ったとき、有限オートマトンではカッコが正しく閉じているかどうか原理的に判定できないです(反覆補題でググれば証明は出てくると思います)。

チューリングマシン

上で出した有限オートマトンの例では、計算能力が限られすぎて面白くなかったかもしれませんが、この延長上でチューリングマシンというものを考えることができます。

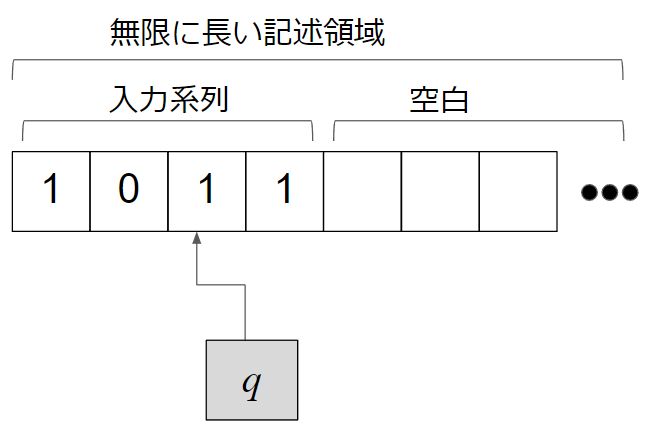
いま、無限に長いメモ用紙が目の前にあると想像してください。

このテープは一定間隔ごとに区切られていて、各区間につき１つずつ記号を記載していくことができます。

チューリングマシンには読み書き用のヘッドがついていて、このメモ用紙にある記号を規則に沿って書き換えていきます。

メモ用紙の先頭からいくらかは入力を書くところになっていて、チューリングマシンはこれを先頭から見ていて書き換えていきます。

基本的なルールは以下のとおりです。

記述領域を自由に書き換えられる(入力が記されているところを書き換えてもOK)
読み書きヘッドが今見ている記号を書き換えたあと(書き換えなくてもOK)、左右どちらかに移動し、チューリングマシンの内部状態が遷移する
ヘッドの移動と書き換えを繰り返し、内部状態が受理常態または非受理状態になれば計算終了

チューリングマシンは内部状態というものを持っていて、ヘッドが見ている記号と内部状態の組み合わせによって、次のアクションが決まります。

内部状態には「受理状態」か「非受理状態」があって、どちらかの状態になった時点で計算が終了します。

非常に単純な機械です。

基本的に、1つのチューリングマシンは、1つの計算しか実行できません。

例えば、「足し算をするチューリングマシン」、「掛け算をするチューリングマシン」、みたいな感じです。

ただ、「チューリングマシンを記号化したもの」を入力として受け取ることで、そのチューリングマシンの行う計算を実行することができるような、特別なチューリングマシンを考えることができます。

この図で$[M]$と書いてあるのは、あるチューリングマシン$M$を記号化したものです。

$[M]$と入力系列を入力されると、$M$の動作を模倣して計算を行います。

これは万能チューリングマシンと言われているもので、任意のチューリングマシンの計算を実行できる、すなわち、あらゆる計算を実行できるようなものになっています。

何かしら計算モデルがあったとして、その計算モデルが万能チューリングマシンを模倣することができるとき、その計算機はチューリング完全だと言ったりします。

JavaやPythonなどのプログラミング言語はもちろんチューリング完全ですし、意外なところでチューリング完全だと知られているものは結構あります(マイクラとかMTGとか)。

うっかりチューリング完全になっちゃったもの

チューリングマシンの特筆すべき性質として、

計算可能なあらゆる関数を実行することができる

というか、チューリングマシンを使って実行できる手順をもって、「計算」とみなそうという話です。

計算できること、できないこと

雑に言うと、計算可能な問題とは、チューリングマシンで実行できる問題のことです。

チューリングマシンを使えば、機械的な操作で実行可能なあらゆる問題を解決できますが、それでも限界があることを見ていこうと思います。

チューリングマシンで解決できない問題の一例として、停止問題を考えます。

停止問題
- 任意のチューリングマシンが与えられたとき、そのチューリングマシンの計算が無限ループするかどうかを判定可能か？

この停止問題が計算不能であることを示していきます。

いま、可能なすべてのチューリングマシンの集合を${M_0, M_1, ..., M_t, ...}$とおきます。

各$M_i$は、チューリングマシンを記号化した系列$[M_j]$を入力として受け取ることができます。

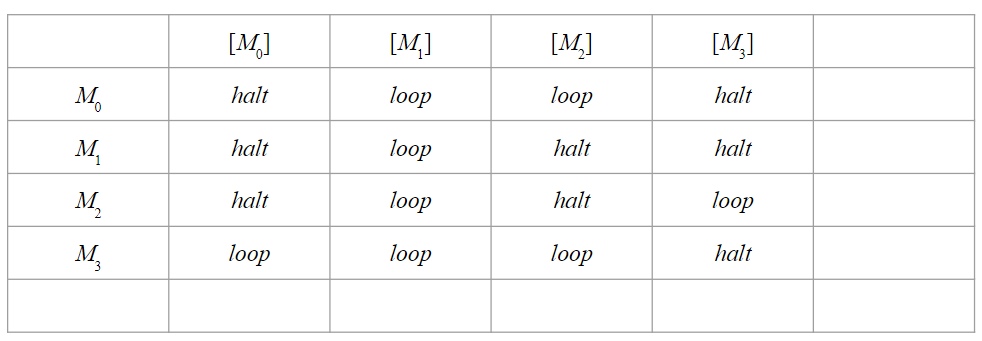
たとえば$M_i$に$[M_j]$を入力として与えたとき、その結果はループする($=loop$)か停止する($=halt$)のどちらかになります。

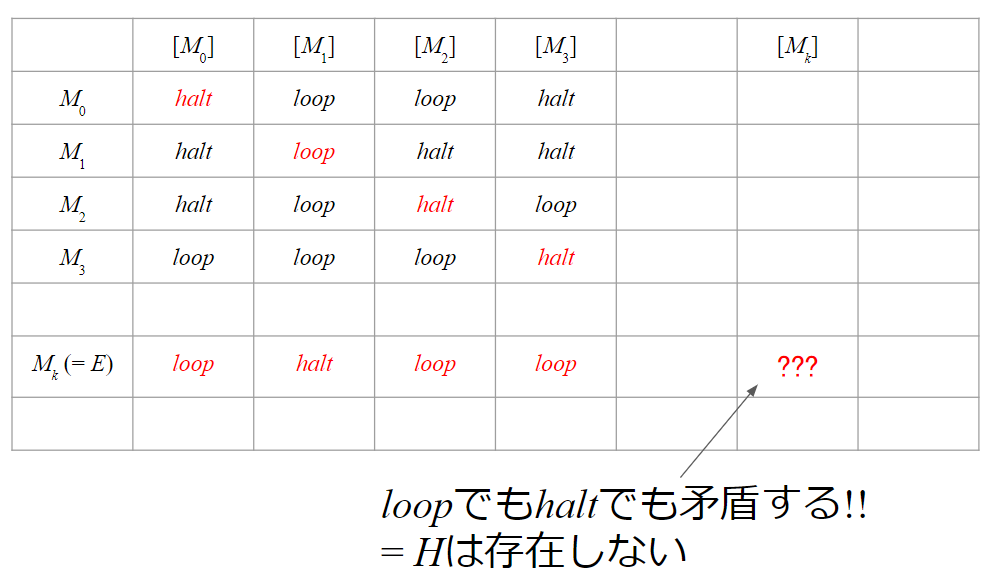
これを表として表すと、以下のようになります。

ここで、系列$[M_i]$を入力として受け取ったとき、$M_i$がループするならば非受理、停止するならば受理するようなチューリングマシンの存在を仮定し、これを$H$とします。

$H$は、チューリングマシンがループするかどうかを有限時間で判定できるので、停止問題を計算することができます。

この$H$の存在からの議論で矛盾を導き、停止問題が計算不能だと示します。

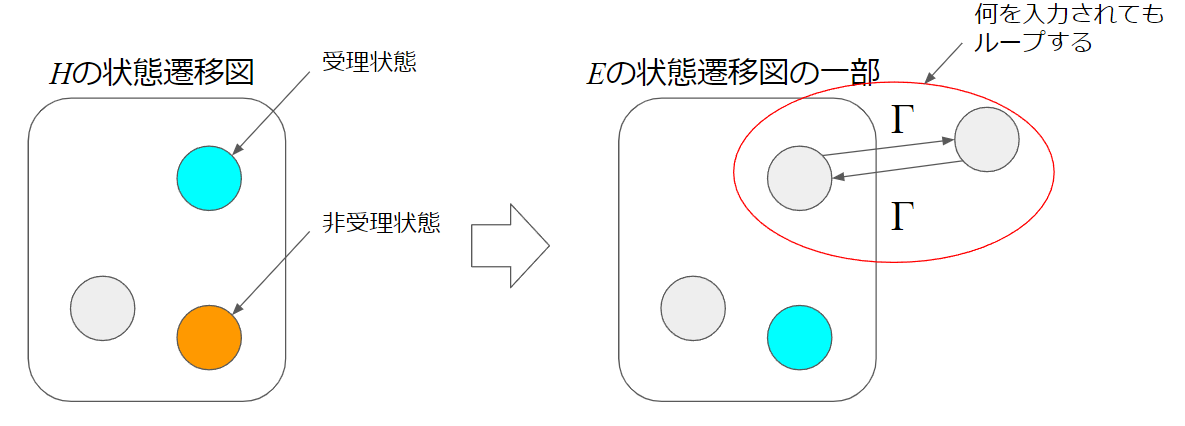
$H$を利用することで、あるチューリングマシンを構成することが可能になります。

そのチューリングマシン$E$は、$M_i$に$[M_i]$を入力した結果が$loop$ならば$halt$、$halt$ならば$loop$となります。

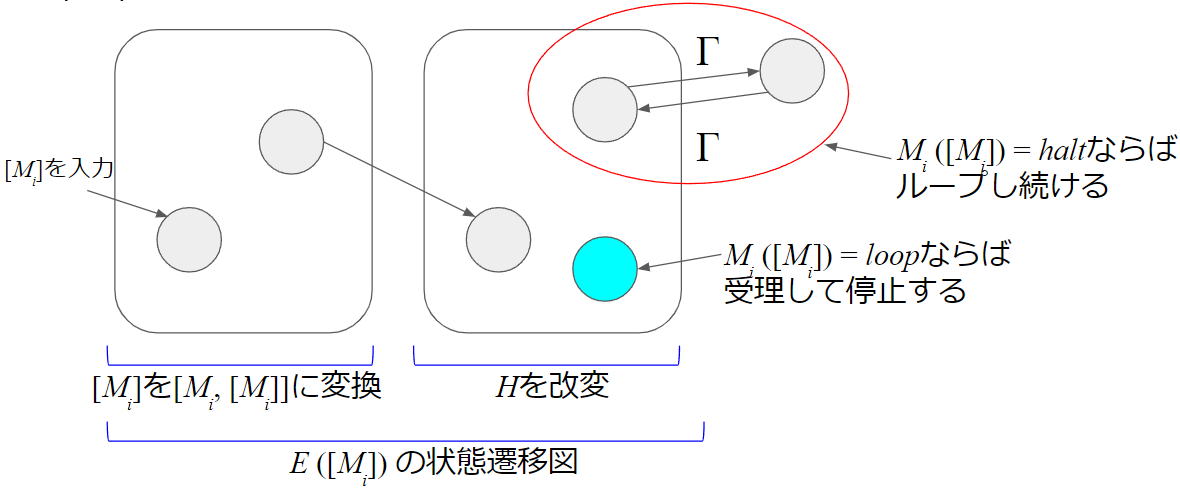
これは$H$の状態遷移図に1つだけ状態を追加して、以下のように改変したものです。

$E$の全体像としては、以下のようになります。

この$E$は、先程の${M_0, M_1, ..., M_t, ...}$のどこかに含まれているはずで、これを$M_k$としましょう。

この$M_k$に$[M_k]$を入力したとき、結果はどうなるでしょうか。

$M_k([M_k])$の結果とは正反対の結果を返さなければならないので、$loop$だろうが$halt$だろうが矛盾することが分かると思います。

ということで無事、停止問題が計算不能だと背理法で示すことができました。

計算不能問題の例

計算不能な問題は、停止問題に帰着できることが知られています。

そんな計算問題の例としていくつか挙げると、

４辺が異なる色で塗られたタイルの隣接する辺の色が等しくなるようにタイルを全平面に敷き詰められるか？
プログラムAはプログラムBと完全に同じ動作をするか？ (仕様通りに動くか？)
プログラムが無限ループするか？
整数係数の多変数方程式は整数解を持つか？
$(u_1, v_1), (u_2, v_2), ...$のペアを並び替えて、$u$を連ねた系列と$v$を連ねた系列を一致させることができるか？

まとめ

チューリング完全と停止問題について説明しました。

全然推敲してないので分かりづらいところもあるかと思いますが、どうかご容赦ください。

チューリング完全ってなんなのさ