#あいさつ
みなさんこんにちは、ゆずっこです。五月祭や駒場祭、パズルスクエアなどで細々とパズルを作っております。最近ではパズルボスラッシュでお世話になった方もいると思います。その節はどうもご迷惑をおかけしました。
さて、最近パズルスクエアでアゼンのましゅを連投しているわけですが、これらに大体共通する手筋の解説をしたいと思います。タイトルにあるとおり「内外」と呼んでいるものです。
#導入
マスの中央に線を引きループを作るパズルにおいて、各格子点はループの中と外に分けられます。ここではペンパくんの仕様上「出入」で表記しますが…
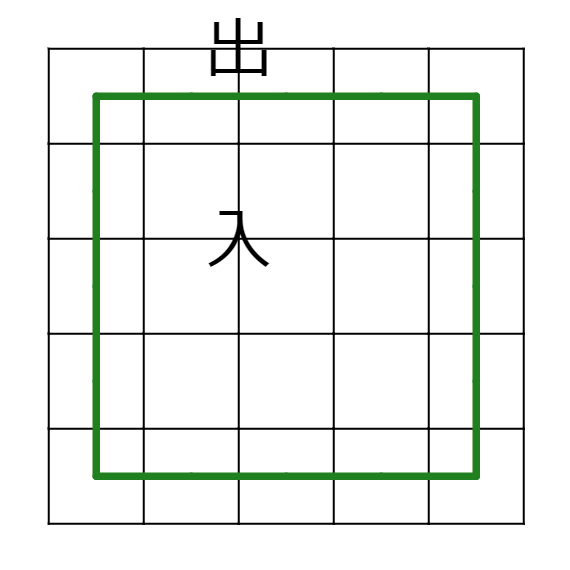
このように分けることの何が良いかというと、隣り合う格子点で内外が決まった時に線が引かれる・引かれないということが決定するのです。
つまりこれが…
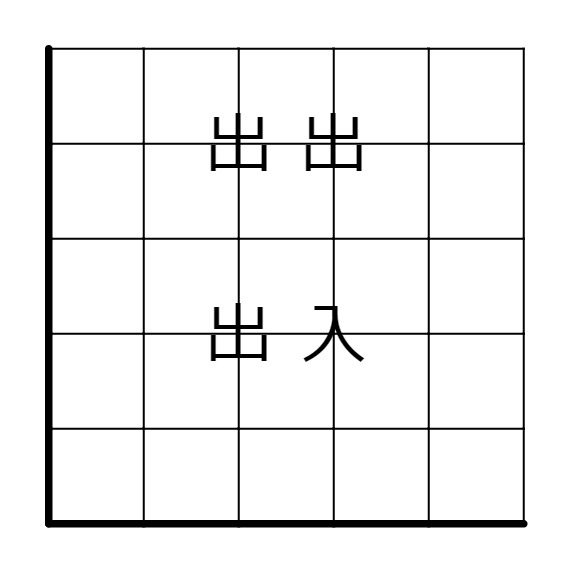
このようになります。
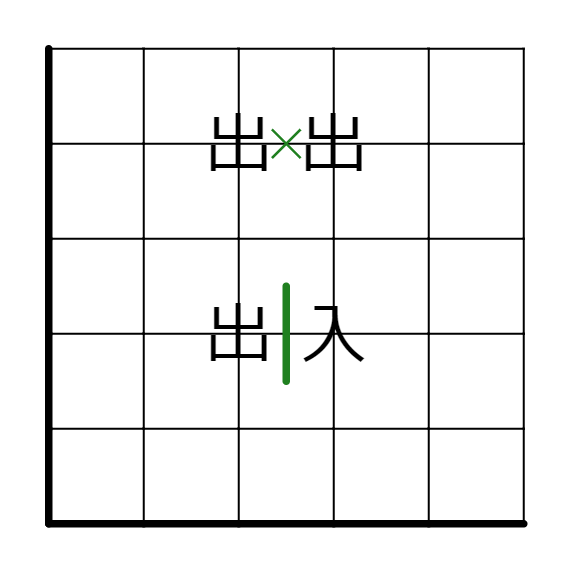
この理論はましゅと非常に相性がいいのです。
#利用
白丸を見てみましょう。
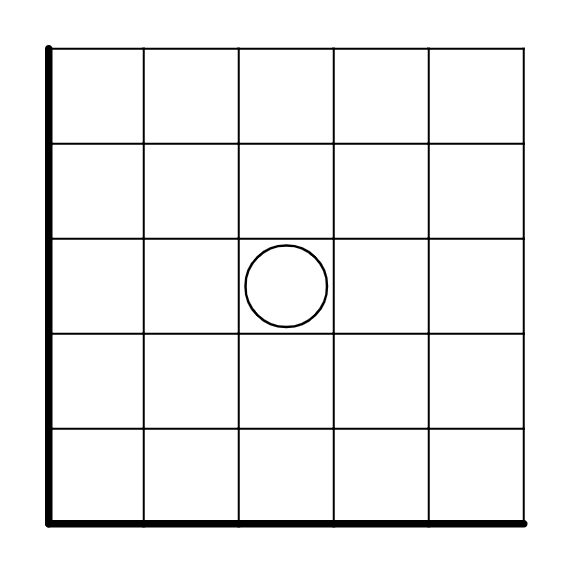
ルールから白丸には線が一本まっすぐに通ります。つまりこれらのどっちかになるというわけです。
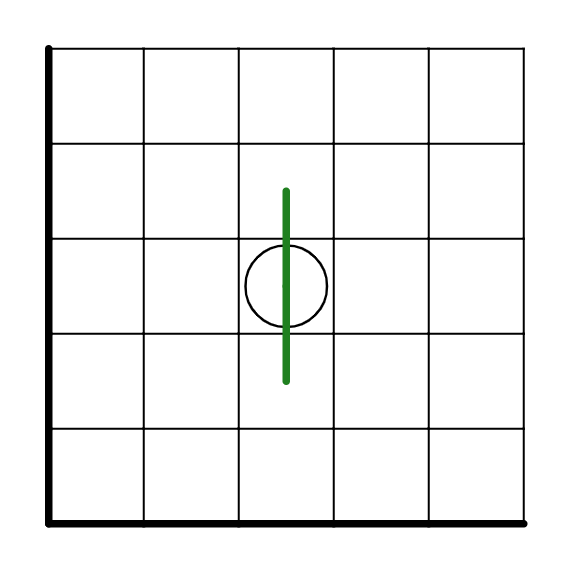
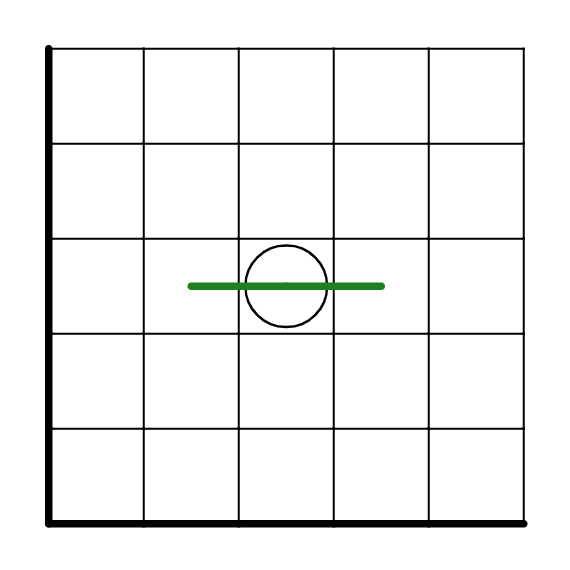
ここで、白丸をナナメにはさむ格子点は内外が反転することがわかります。ここでは中か外かが不明なのでAとBとします。
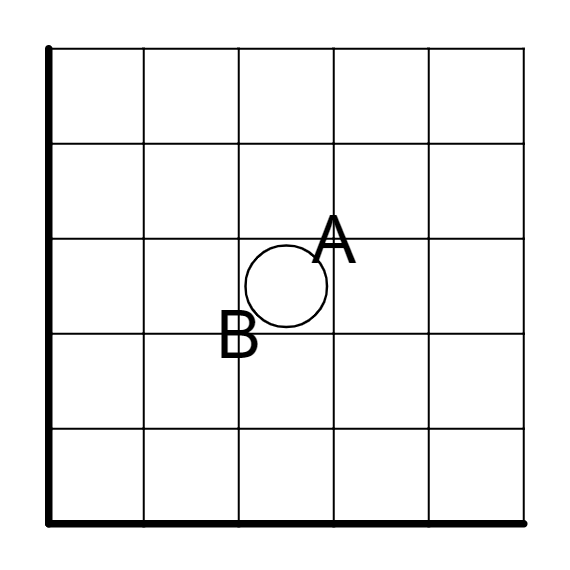
これを利用すると次のようなことができます。このようにナナメにつながった白丸があると、
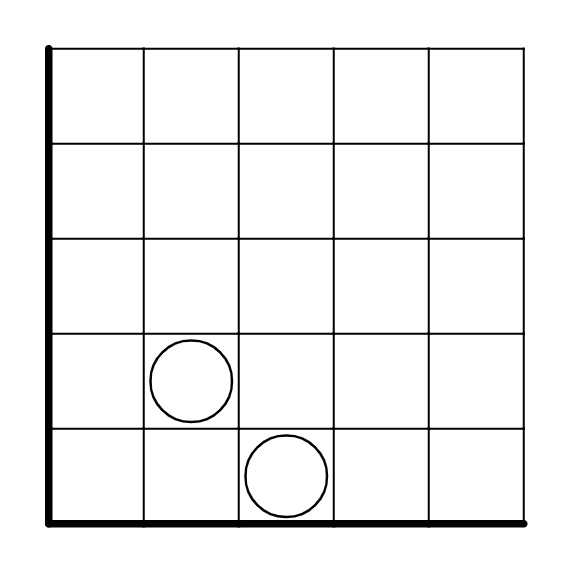
内外が決定し、
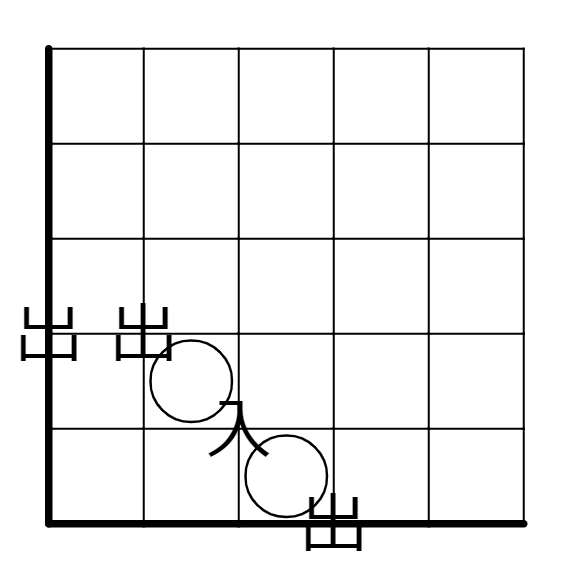
線が引かれないことが決定します。
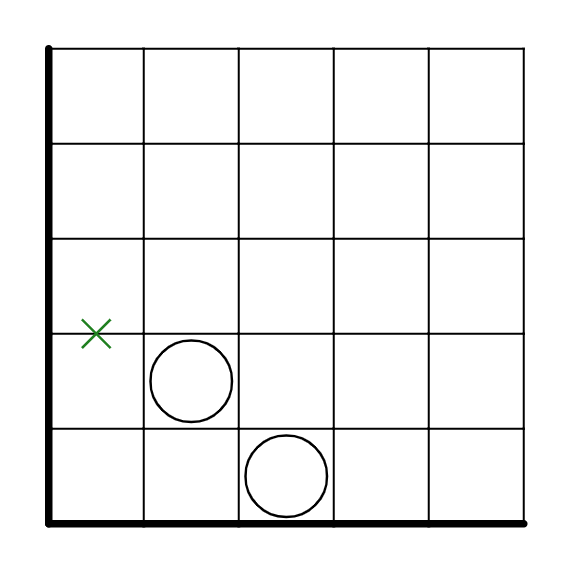
応用は壁際に限らず、出現の仕方も非常に多岐にわたりますが、ぼくの作ったましゅを解くと何か見えてくるかもしれません。
また、2019年駒場祭で出したハバネロましゅパズスクのリンクはこちらもこれを利用しており理詰めで解ける問題となっているので挑戦してみてください。
#雑記
この理論は偶数端点と本質的には同じなのですが、ことましゅにおいては偶数端点と比較して追いやすくまた絶大な効果を発揮する理論となります。
ただし、これが必須であるとまず難易度がアゼン程度になり、ニコリには絶対に載らないのでご注意ください。
この理論はループ系パズル全般で使用できますが、その応用はここでは記述しません。
#謝辞
この理論を(めっちゃ昔に)教えてくれたしもりんにこの場を借りて多大な感謝を申し上げます。ありがとうございます。