はじめに
マッチングアプリ等を皮切りに実生活の至る所で用いられているマッチング問題。
今回はその中の一種、二部グラフにおけるマッチング問題の典型的な問題をFord-Fulkerson法で解いてみました。
二部グラフや二部マッチング問題とはなんぞやという話から、二部マッチングの典型問題鉄則本a69 の実装について述べます。
二部グラフとは
二部グラフは、
数学、とくにグラフ理論における2部グラフ(にぶグラフ、英: bipartite graph)とは、頂点集合を2つに分割して各部分の頂点は互いに隣接しないようにできるグラフのことである。
(wikipedia)
とのことです。つまり、以下のように同じ色のグループ同士では辺を持たないグラフを指します。

二部マッチング問題とは
二部グラフが与えられたとき、ペアを作るために同じ頂点から出る辺のうち1つしか選べないという条件下で、全頂点から最大何本の辺を選ぶことができるかを求める問題です。
二部マッチング問題は、例えば以下のように異なる色の頂点でできるだけペアができるようにしたときの本数を求めることです。

この例では、<0, 5>, <1, 7>, <2, 9>, <4, 8>がペアであり、マッチングの最大本数は4となります。
例題 a69
実際に二部マッチングの典型問題鉄則本a69 を解いていきます。
以下図で示す内容は一つ目の入力例に沿っています。
解法のSTEP
青色の頂点を生徒、ピンク色の頂点を椅子とします。
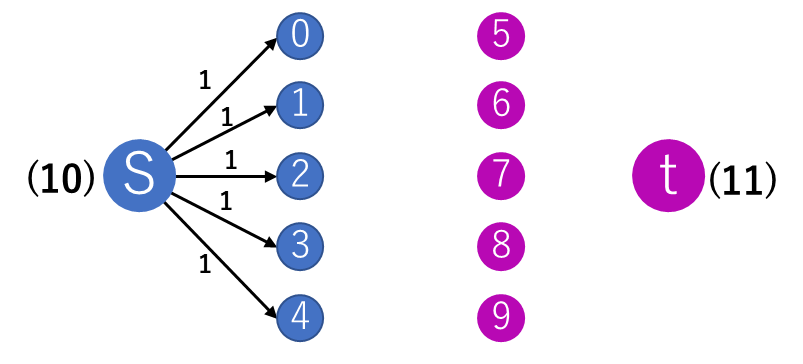
- スタート地点sから青色頂点に向かう辺を追加
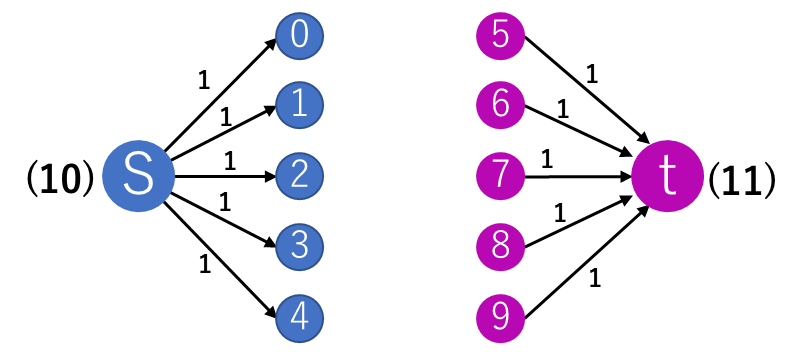
- ピンク色頂点からゴール地点tに向かう辺を追加
- 問題の内容から青色頂点からピンク色頂点に向かう辺を追加
- フォードファルカーソン法によって、s→tへの最大流を求める
- 解けました!
STEP1 スタート地点sから青色頂点に向かう辺を追加
STEP2 赤色頂点からゴール地点tに向かう辺を追加
STEP1, 2のコード
フルのコードは後に記載しており、ここでは該当部分のみ抜粋します。
repマクロを使用し、FordFulkerson法のクラスのインスタンスをffとしています。
上の図では頂点数nは5であり、sは25, tは25+1と表せます。
rep(i,0,n){
ff.add_edge(2*n, i, 1); //s->青
ff.add_edge(n+i, 2*n+1, 1); //赤->t
}
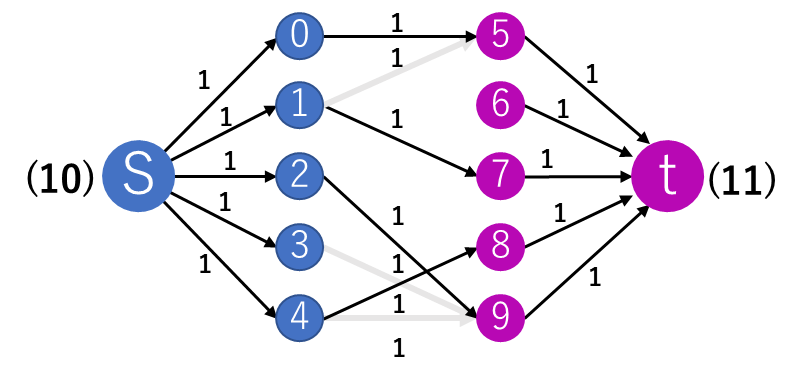
STEP3 問題の内容から青色頂点からピンク色頂点に向かう辺を追加
rep(i,0,n){
rep(j,0,n){
if(s[i][j]=='#'){
ff.add_edge(i, n+j, 1); //from, to, costで辺を生成
}
}
}
青色の頂点とピンク色の頂点で二部グラフは構成することができました。ですが、まだ二部マッチング問題の要件を満たしていません。例えば、0番目の椅子(頂点数としては5番目)は、0番目の生徒と1番目の生徒が座ろうとしている椅子です。ところが、当然どちらか一人しかこの椅子には座れないのでこの状態は不適当です。
STEP4 フォードファルカーソン法によって、s→tへの最大流を求める
STEP3の図で不適当な例としては、既に0番目の生徒が5番の椅子に座っており、1番目の生徒は5番の椅子に座ることは不可能なことでした。換言すれば、s→0→5→tで容量1のフローを流したのち、s→1→5→tと流すことはできず流量は0となります。このように生徒と椅子のマッチング数は、s→tへの流量に置き換えることができます。そこで、二部マッチング問題を解く、すなわち生徒から椅子への最大マッチング本数を求めることは、s→tの最大流を求めることと同義です。つまり、(マッチングの最大本数)=(s→tの最大流)となります。グラフの最大流を求めるアルゴリズムとして有名なフォードファルカーソン法を用いることで、この関係を満たすマッチング本数を求めることができます。
//頂点2*n->2*n+1までの最大流の出力
cout << ff.maxFlow(2*n, 2*n+1) << endl;
フォードファルカーソン法の実装についてはこちら
a69のフルのソースコード
/*FORDFULKERSON*/
#include <iostream>
#include <string>
#include <vector>
#include <unordered_map>
#include <queue>
#include <algorithm>
using namespace std;
#define rep(i, a, b) for (int i = a; i < b; i++)
#define INF (1e9 + 1)
using ll = long long;
using P = pair<ll, ll>;
//辺の構造体
struct Edge {
//rev: toから行ける頂点のうち、toから見てfromが何番目に位置するか
//G[from].size() == rev
int rev, from, to, cap;
};
//フォードファルカーソン法
class FordFulkerson {
public:
vector<vector<Edge>> G;
vector<bool> visited;
// 頂点数 n の残余グラフを用意
int size = 0;
void init(int n) {
G.resize(n);
visited.resize(n);
size = n;
}
/*
頂点 u -> v について 上限 cost の辺を追加
コスト0の逆辺も張る
*/
void add_edge(int u, int v, int cost) {
int u_vID = G[u].size(); // 現時点での G[u] の要素数 = uからみたvのindex
int v_uID = G[v].size(); // 現時点での G[v] の要素数 = vからみたuのindex
G[u].emplace_back(Edge{v_uID, u, v, cost}); //<u,v>の逆辺<v,u>はG[u][v_uID]
G[v].emplace_back(Edge{u_vID, v, u, 0}); //逆辺は追加時はコスト0!!
}
/*
深さ優先探索(F はスタートした頂点からposに到達する過程での "残余グラフの辺の容量" の最小値)
goalまでの往路は頂点を記録しながらs->tまでに共通して流せる容量 = s->tまでの容量の最小値を取得
復路はs->tまでの容量の最小値を使って残余ネットワークのコストを更新
返り値: 流したフローの量
*/
int dfs(int pos, int goal, int F) {
if (pos == goal) return F; //ゴールに到着したら流す
visited[pos] = true; //訪れた頂点を記録
// G[pos]に隣接する頂点を探索
for(auto &e : G[pos]){
//容量0の辺や訪問済みの頂点は無視
if (e.cap == 0 or visited[e.to]) continue;
// 再帰で目的地までのパスを探す
int flow = dfs(e.to, goal, min(F, e.cap));
// 残余ネットワークの更新
// フローを流せる場合、残余グラフの容量をflowだけ増減させる
if (flow > 0) {
e.cap -= flow; //u->vの辺を減少
G[e.to][e.rev].cap += flow; //v->uの辺を増加
return flow;
}
}
return 0;
}
// 頂点sから頂点tまでの最大フローの総流量を返す
int maxFlow(int s, int t) {
int totalFlow = 0;
while (true) {
visited.assign(size, false); //s->tに探索する前に記録した頂点をリセット
int F = dfs(s, t, INF); //s->tへの流量を取得
//フローを流せなくなったら終了
if (F == 0) break;
totalFlow += F;
}
return totalFlow;
}
};
int n, m;
int a,b,c;
FordFulkerson ff;
int main() {
// 入力
cin >> n;
//グラフの作成
ff.init(2*n+2);
vector<string> s(n);
rep(i,0,n){
cin >> s[i];
}
rep(i,0,n){
rep(j,0,n){
if(s[i][j]=='#'){
ff.add_edge(i, n+j, 1); //from, to, costで辺を生成
}
}
ff.add_edge(2*n, i, 1); //s->青
ff.add_edge(n+i, 2*n+1, 1); //赤->t
}
//頂点2*n->2*n+1までの最大流の出力
cout << ff.maxFlow(2*n, 2*n+1) << endl;
return 0;
}