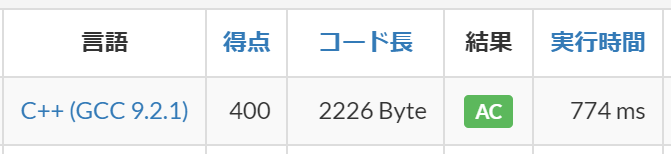
abc285のD問題をBFS(幅優先探索)を使って解いてみました。
言語はC++です。
UnionFindやDFSを使った別解はこちら。
Point
-
a → b → c → aと一巡したらダメそう
- グラフ理論でいうところのサイクル(閉路)があるかどうかを検出
- 探索した頂点をmemoすることでTLE対策
-
BFS(幅優先探索)で全頂点を探索してサイクルがあるかを検出
- 既にvisitedな頂点に再度訪問 -> サイクル有り
a------>b------>c 既に訪問済みの頂点aに対し、aに再訪問するとサイクルができる ^---2回目のa---| - 解けました!
コード例
d_bfs.cpp
#include <iostream>
#include <string>
#include <vector>
#include <unordered_map>
#include <atcoder/all>
using namespace std;
using namespace atcoder;
#define rep(i, a, b) for (int i = a; i < b; i++)
int n;
using Graph = unordered_map<string, vector<string>>; //グラフ作成
Graph G;
unordered_map<string, bool> visited; //訪問済みかどうか
unordered_map<string, bool> memo; //TLE対策で訪問済みの頂点をメモ
queue<string> que; //BFSの要
//サイクルが存在すればtrue, 無ければfalseを返す
bool bfs(string start) {
que.push(start); //探索の起点となる頂点を筒に入れる
while(!que.empty()){ //筒が空になるまで≒前頂点の探索が終了するまで
string s = que.front(); //筒の先頭を保持
que.pop(); //筒から先頭を取り出す
visited[s] = true; //先頭を探索済みに
for(auto v : G[s]){ //先頭の頂点に隣接する頂点について、探索済みか否かを判定
memo[v] = true; //探索済みの頂点として記録
if(visited[v]) {
return true; //探索済みの頂点であれば、サイクルが存在
//ex. a---->b---->c---->aは 最初のaでvisited[a]=trueなので、
// a---->b---->c 二回目のaではサイクルができる
// ^-----------|
}
que.push(v); //先頭に隣接する頂点を筒に格納(次の先頭の候補とする)
}
}
return false;
}
int main(){
cin>>n;
vector<string> s(n), t(n);
rep(i,0,n){
cin >> s[i] >> t[i];
//s->tのグラフを作成
G[s[i]].emplace_back(t[i]);
}
rep(i,0,n){
string start = s[i];
if(memo[start]) continue; //探索済みの頂点であればTLE対策で無視
bool closed = bfs(start); //BFSでサイクル判定
if(closed) {
cout << "No" << endl;
return 0;
}
visited.clear(); //複数のグラフが存在する可能性があるので毎回初期化
}
cout << "Yes" << endl;
return 0;
}
解けました!