きっかけは、自分が過去に書いたプログラムを整理していると、ベジェ曲線のカーブフィッティング(曲線あてはめ)をするJavaScriptが出てきて、懐かしいなーと思って読んでみたのですが数式が難しすぎて全く理解できませんでした。
何でこんな謎の数式で近似できるねん、昔の俺すげーな。
どうやら最小二乗法を使って近似していたようです、復習がてらPythonで説明したいと思います。
参考書をひっぱりだして勉強しなおしました、ちなみに参考文献は金谷健一先生の「これなら分かる最適化数学―基礎原理から計算手法まで」です。非常に解りやすく解説されている本でオススメです。
最小二乗法とは何なのか?
最小二乗法とは、複雑なデータや関数を近似する代表的な手法で、データ解析における最も重要な基礎となります。
適用範囲は非常に広く、微分可能であればどんな関数も近似が可能という実用性と美しさを兼ね備えた手法です。
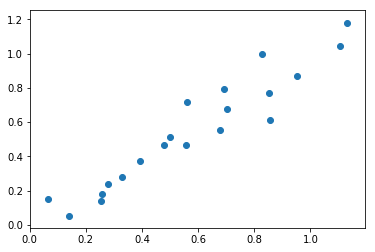
例えば、ここに20個の点があったとします。
20個の点に対して最も近い場所を通る直線を置いてみましょう。
直線の関数$f(x) = ax + b$について、すべての点に最も近い場所を通るパラメータ$a$,$b$を求めます。
この$a$,$b$を求める代表的な方法が最小二乗法なのです。
指定の場所とプロットした場所の誤差を二乗した総和が最小になるように近似するので、最小二乗法と呼びます。
直線の近似
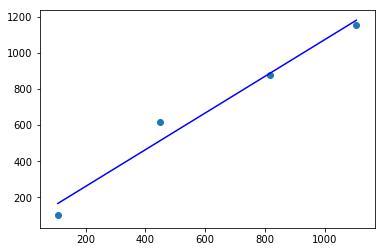
まずは、一番簡単な直線の近似をやってみましょう、以下の4点を近似する直線を引いてみます。
points = [(107, 101), (449, 617), (816, 876), (1105,1153)]
直線の関数は$f(x) = ax + b$です、$a$が傾きで$b$が切片ですね。
関数$f(x)$に対して、指定の点の誤差の二乗が最小になるパラメータ$a$と$b$を求めます。
指定の場所$y$とすると、誤差の二乗を求める関数$j(x, y)$は以下のようになります。
j(x, y) = (y - (ax + b))^2
N個の点に対して$j$の総和が最小になればよいので、最小二乗法の式は以下のようになります。
J = \frac {1}{2}\sum_{k=1}^{n} j(x_k, y_k)
誤差関数j(x, y)の偏導関数を求める
いきなり難解ワードの偏導関数が出てきましたが、何も心配ありません。
計算方法さえ判れば小学生でも計算できます。
2つ以上の変数がある関数をある1つの変数について微分することを偏微分と言います。
そして、偏微分によって求められた関数を偏導関数と言います。
微分を忘れた人用の説明
微分は、$(X^n)' = nX^{n-1}$で、指数をnを係数にして指数をn-1するやつです。
例:
$(x^2)' = 2x$
$(2x^2)' = 4x$
$(4x^3)' = 12x^2$
微分はグラフの接線の傾きとなります、グラフの瞬間の速度を求めると言い換える事もできます。
微分が0の点は、凸のグラフの場合は変曲点となります。
Sympyを使って偏微分を求める
微分が解れば偏微分も別に目新しい事もないのですが、難しい事は解らなくても平気です。
我々にはSympy(とJupyter)があるのです!
Sympyを知らない人はSympy+Jupyterで最強の電卓環境を作るをどうぞ。
さっそくJupyterを起動しましょう。
from sympy import *
init_session()
これでSympyとJupyterのセットアップは完了です。
誤差を求める関数$j$を定義します。
a, b = symbols("a b")
j = (y - (a * x + b)) ** 2
sympy.diff関数で偏微分を求める事ができます、まずは$a$について偏微分します。
$a$についての偏導関数は$\frac{\partial j}{\partial a}$、$b$については$\frac{\partial j}{\partial b}$と書きます。
j_a = diff(j, a)
j_b = diff(j, b)
\frac{\partial j}{\partial a}
=
- 2 x \left(- a x - b + y\right) \\
\frac{\partial j}{\partial b}
=
2 a x + 2 b - 2 y
直線関数の偏導関数が求めることができました、Sympyがあれば楽勝ですね。
最小二乗法は誤差の総和の1/2なので計算してみましょう。
式への値の代入はsympy.subs関数で行います。
sum_a = sum([j_a.subs([(x, _x), (y, _y)]) for _x, _y in points]) / 2.
sum_b = sum([j_b.subs([(x, _x), (y, _y)]) for _x, _y in points]) / 2.
\frac {1}{2}\sum_{k=1}^{n} \frac{\partial j}{\partial a}
=
2099931.0 a + 2477.0 b - 2276721.0 \\
\frac {1}{2}\sum_{k=1}^{n} \frac{\partial j}{\partial b}
=
2477.0 a + 4 b - 2747.0
各総和の1/2の式が出ましたね、あとはこの2つの式の連立方程式を解くだけです。
\begin{bmatrix}
2099931.0 & 2477.0 \\
2477.0 & 4
\end{bmatrix}
\begin{bmatrix}
a \\
b
\end{bmatrix}
=
\begin{bmatrix}
2276721.0 \\
2747.0
\end{bmatrix}
solve([sum_a, sum_b], [a, b])
# {a:1.01694642025091,b:57.0059292596265}
a=1.01694642025091、b=57.0059292596265が答えです。直線の方程式$y = ax + b$に代入すれば良いのです。
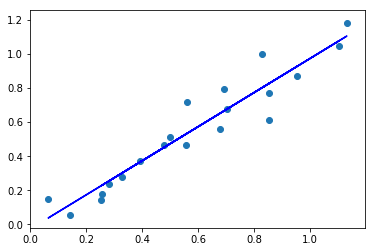
さっそくプロットしてみましょう。
直線のため全ての点を通過できていませんが、それに近しい場所を通っています。
ベジェ曲線の近似
先程は単純な直線を近似しましたが、3次曲線のベジェ曲線も全く同じ手順で近似できます。
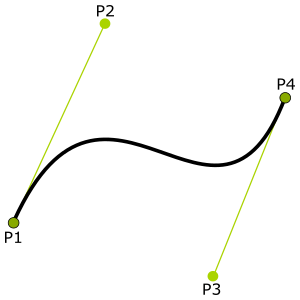
ベジェ曲線は、$p_1$は始点、$p_4$は終点、$p_2$と$p_3$がそれぞれコントロールポイントとなります。
3次ベジェ曲線の式は以下のとおりです。
bz = p_{1} \left(- t + 1\right)^{3} + p_{2} t \left(- 3 t + 3\right) \left(- t + 1\right) + p_{3} t^{2} \left(- 3 t + 3\right) + p_{4} t^{3}
tの範囲は0 ≦ t ≦ 1です。
ベジェ曲線の式を$bz$とし、近似したい点を$p_x$とすると、誤差を求める関数$j$は以下のようになります。
j = (p_x - bz)^{2}
最小二乗法の定義は以下のとおりでしたね。
J = \frac {1}{2}\sum_{k=1}^{n} j(x_k, y_k)
求めたいパラメータは$p_2$と$p_3$ですので、それぞれのパラメータで偏微分します。
最小二乗法の定義の1/2がありますので、偏導関数に1/2をあらかじめ掛けてしまいましょう。
さっそくSympyで書いてみましょう。
p0, p1, p2, p3, p4, px, t = symbols("p0 p1 p2 p3 p4 px t")
bz = (1-t)**3*p1 + 3*(1-t)**2*t*p2 + 3*(1-t)*t**2*p3 + t**3*p4
j = (px - bz) ** 2
jp2 = simplify(diff(j, p2) / 2)
jp3 = simplify(diff(j, p3) / 2)
$p_2$と$p_3$の偏導関数の1/2は、それぞれ以下のようになります。
\frac{1}{2} \frac{\partial j}{\partial p_2}
=
3 t \left(t - 1\right)^{2} \left(- p_{1} \left(t - 1\right)^{3} + 3 p_{2} t \left(t - 1\right)^{2} - 3 p_{3} t^{2} \left(t - 1\right) + p_{4} t^{3} - px\right)
\\
\frac{1}{2} \frac{\partial j}{\partial p_3}
=
3 t^{2} \left(t - 1\right) \left(p_{1} \left(t - 1\right)^{3} - 3 p_{2} t \left(t - 1\right)^{2} + 3 p_{3} t^{2} \left(t - 1\right) - p_{4} t^{3} + px\right)
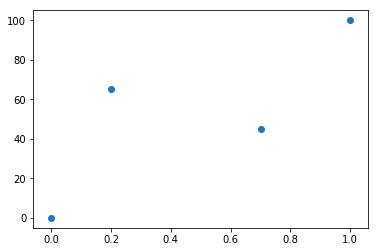
通過させたい点$p_x$と、その時に$t$のペア値を定義します、例として以下の4点があるとします。
points = [(0, 0), (0.2, 65), (0.7, 45), (1.0, 100)]
始点と終点が$p_1$と$p_4$になりますので、この2つは既知の値となります。
求めたい$p_2$と$p_3$について、偏導関数の総和を連列方程式で解きます。
const = ((p1, points[0][1]), (p4, points[-1][1]))
tp2 = sum([jp2.subs(const + ((t, x[0]), (px, x[1]))) for x in points[1:-1]])
tp3 = sum([jp3.subs(const + ((t, x[0]), (px, x[1]))) for x in points[1:-1]])
solve([tp2, tp3], [p2, p3])
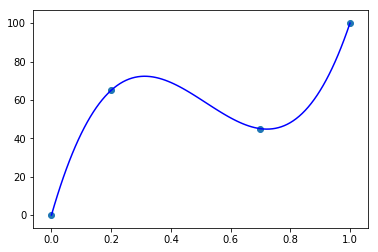
# {p2:180.456349206349,p3:−53.0753968253968}
答えはp2=180.456349206349,p3=−53.0753968253968です。
ちゃんと近似できていますね!
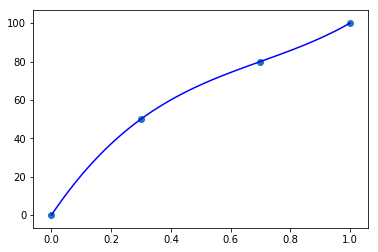
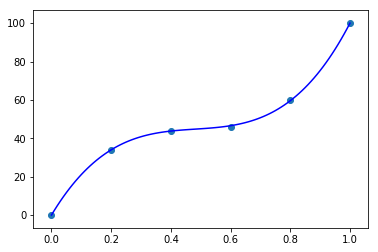
色々なパラメータを見てみましょう。
points = [(0, 0), (0.3, 50), (0.7, 80), (1.0, 100)]
points = [(0, 0), (0.2, 34), (0.4, 44), (0.6, 46), (0.8, 60), (1.0, 100)]
あまり極端な値でない限り、ちゃんと通過できるようです。
もちろん通過できない値もありますが、なんとなくそれっぽく線を引いてくれます。
いろいろな曲線を生成してみる
最後にJupyter上でベジェ曲線を最小二乗法で近似して、プロットするセルを記載します。
%matplotlib inline
import matplotlib.pyplot as plt
p0, p1, p2, p3, p4, px, t = symbols("p0 p1 p2 p3 p4 px t")
bz = (1-t)**3*p1 + 3*(1-t)**2*t*p2 + 3*(1-t)*t**2*p3 + t**3*p4
j = (px - bz) ** 2
jp2 = simplify(diff(j, p2) / 2)
jp3 = simplify(diff(j, p3) / 2)
def plot(points):
const = ((p1, points[0][1]), (p4, points[-1][1]))
tp2 = sum([jp2.subs(const + ((t, x[0]), (px, x[1]))) for x in points[1:-1]])
tp3 = sum([jp3.subs(const + ((t, x[0]), (px, x[1]))) for x in points[1:-1]])
vec = solve([tp2, tp3], [p2, p3])
const = {p1: points[0][1], p2: vec[p2], p3: vec[p3], p4: points[-1][1]}
bz2 = bz.subs(const)
x = np.arange(0, 1+0.01, 0.01)
y = [
bz2.subs(t, _t)
for _t in x
]
plt.plot(x, y)
plt.scatter([p[0] for p in points], [p[1] for p in points])
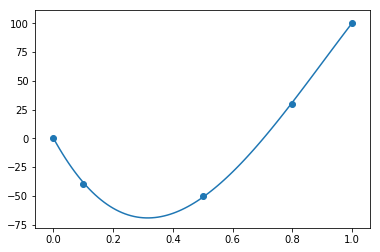
plot関数に通過して欲しい点のリストを入力すると、最小二乗法で頑張ってその点を通ってくれます。
使い方は以下のように呼びます。
points = [(0, 0), (0.1, -40), (0.5, -50), (0.8, 30), (1.0, 100)]
plot(points)
Sympyを使わないで解く
C/C++などSympyがない環境での実装を書きます。
\frac{1}{2} \frac{\partial j}{\partial p_2}
=
3 t \left(t - 1\right)^{2} \left(- p_{1} \left(t - 1\right)^{3} + 3 p_{2} t \left(t - 1\right)^{2} - 3 p_{3} t^{2} \left(t - 1\right) + p_{4} t^{3} - px\right)
\\
\frac{1}{2} \frac{\partial j}{\partial p_3}
=
3 t^{2} \left(t - 1\right) \left(p_{1} \left(t - 1\right)^{3} - 3 p_{2} t \left(t - 1\right)^{2} + 3 p_{3} t^{2} \left(t - 1\right) - p_{4} t^{3} + px\right)
とはいえ、使用するのは上の算出済みの2式だけで、不明な点$p_2$と$p_3$を1.0と置き、各項ごとに計算しているだけです。できるだけC/C++っぽく書いてみます。
def lsm(points):
''' 最小二乗法の解を行列で返す '''
p1, p4 = points[0][1], points[-1][1]
a = b = c = d = e = f = 0.
for _t, _px in points[1:-1]:
_t_1_d = (_t - 1.) ** 2
_t_1 = (_t - 1.)
_p1 = p1 * _t_1
_p2 = 3 * _t * _t_1_d
_p3 = 3 * _t ** 2 * _t_1
_p4 = p4 * _t ** 3
_j_p2 = 3 * _t * _t_1_d
_j_p3 = 3 * _t ** 2 * _t_1
a += _p2 * _j_p2
b += -_p3 * _j_p2
c += -_p2 * _j_p3
d += _p3 * _j_p3
e += -((-_p1 + _p4 - _px) * _j_p2)
f += -((_p1 - _p4 + _px) * _j_p3)
return [
[a, b],
[c, d]
], [e, f]
def inv(mat, vec):
''' 逆行列で連立方程式を解く '''
dm = mat[0][0] * mat[1][1] - mat[1][0] * mat[0][1]
assert (dm != 0.0)
a = mat[1][1] / dm
b = -mat[0][1] / dm
c = -mat[1][0] / dm
d = mat[0][0] / dm
return (vec[0] * a + vec[1] * b,
vec[0] * c + vec[1] * d)
points = [(0, 0), (0.2, 65), (0.7, 45), (1.0, 100)]
inv(*lsm(points))
あとがき
最小二乗法は、微分可能な関数であれば近似可能という非常に強力な手法です。
ベジェ曲線の近似はゲームプログラムに応用すると楽しそうですね。
偏導関数を事前にSympyで計算しておけば、C/C++などの他言語でも連立方程式を解くアルゴリズムを実装するだけで計算できます。
(連立方程式は「ガウスジョルダンの掃き出し法」など、沢山のアルゴリズムがあります)
やはりSympyは非常に強力なツールですね、変数が多い数式も簡単に最適化/計算してくれます。
計算が苦手なので非常に重宝しています。