AtCoder B,C問題をKotlinで解こう - ABC266

当記事ではAtCoder、ABCのB問題ならびにC問題（時々D問題も）のKotlinでの解法を超初心者向けに詳細に解説します。

B - Modulo Number

やりたいこと

$n - x = (998244353 の倍数)$ ということは、x = n % 998244353 となることが分かる。ただし、nの値はマイナスであることもあるため、n % 998244353 がマイナスになる場合もある。
n % 998244353を計算し、結果が0以上である場合はそのまま答えとして出力し、0未満である場合は結果に998244353を加えて出力 しよう。

入力値の取得

    // 入力値の取得
    val n = readLine()!!.toLong()

サンプルコード

main.kt

fun main(args: Array<String>) {
    // 入力値の取得
    val n = readLine()!!.toLong()

    val target = 998244353

    var ans = n % target

    if (ans < 0) {
        // マイナスであった場合は 998244353 を加える
        ans += target
    }
    println(ans)
}

C - Convex Quadrilateral

やりたいこと

異なる3点ABCを 時計回りに 見た場合

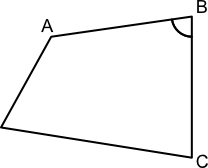
$∠ABC$ が180°以上の場合以下が成立する。
(A.x-B.x)*(C.y-B.y) - (A.y-B.y)*(C.x-B.x) <= 0
入力値は反時計回りで与えられるため、入力値を取得後逆順にし、全ての隣接する3点について判定を行おう。

入力値の取得

    // 入力値の取得
    val points = (1..4).map { readLine()!!.split(" ").map { it.toInt() }.let { Point(it[0], it[1]) } }.reversed()

サンプルコード

main.kt

import java.awt.Point

fun main(args: Array<String>) {
    // 入力値の取得
    val points = (1..4).map { readLine()!!.split(" ").map { it.toInt() }.let { Point(it[0], it[1]) } }.reversed()

    // 全ての隣接する3点について、それが作る角が180°以上になるものが存在するかどうかを判定
    val ans = points.indices.all { !isAngOver180(points[it], points[(it + 1) % 4], points[(it + 2) % 4]) }

    // 答えの出力
    println(if (ans) "Yes" else "No")
}

// 異なる3点の作る角が180°以上になるかどうかを判定
fun isAngOver180(p1: Point, p2: Point, p3: Point): Boolean {
    val fixP1 = Point(p1.x - p2.x, p1.y - p2.y)
    val fixP3 = Point(p3.x - p2.x, p3.y - p2.y)
    return fixP1.x * fixP3.y - fixP1.y * fixP3.x <= 0
}