概要
この記事はkaggle advent calendar 2019の20日目の記事になります。
最近、データ分析に入門しいろいろと勉強しています。
その中で、データ分析のステップの一つとして、外れ値検出、という作業があることを知り、
今回その内容についてまとめてみました。
ちなみに、numpyとpandasもあまり使用経験がありませんので、もし変なことをしている場合は、
ご指摘頂ければ幸いです。
ちなみに、記載しているコードはGoogle Colaboratoryで実際に動かす事が可能です。
では、よろしくお願いします。\(^o^)/
手作業による外れ値の検出
はい。
まずは、ここから始めます。
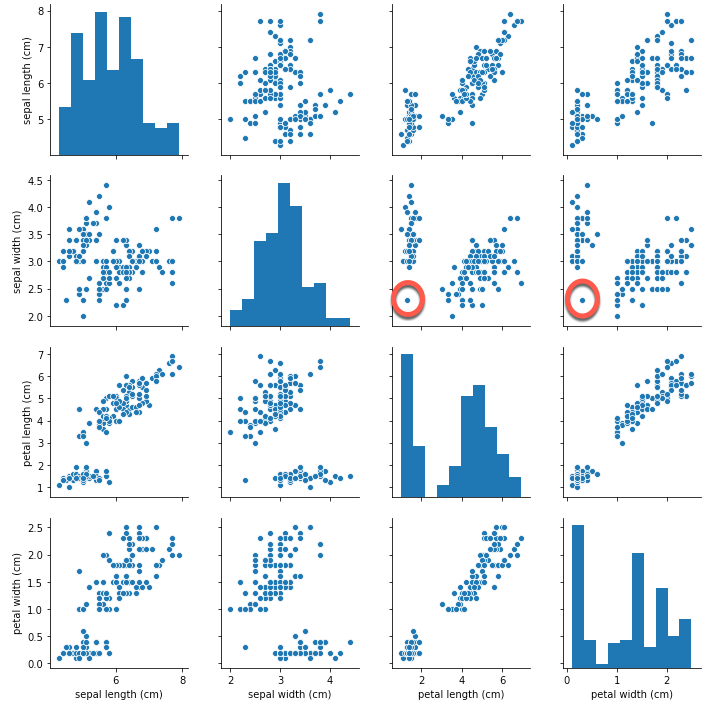
実際のデータをグラフにして、データの内容を把握し、外れ値がどのような状態なのかを確認します。
例えば、アヤメのサンプルデータについて、変数同士の関係を見てみましょう。
from sklearn.datasets import load_iris
import seaborn as sns
import pandas as pd
iris_dataset = load_iris()
df = pd.DataFrame(iris_dataset.data, columns=iris_dataset.feature_names)
sns.pairplot(df)
可視化することで、例えば丸をつけたデータが、外れ値では?、ということを見つけることが出来ます。
1次元データの外れ値の検出
次に1次元データの外れ値の検出についてです。
いろいろな方法があるかとは思うのですが、今回は四分位数の考え方を利用して、外れ値の検出を行います。
四分位数とは、データの個数に着目し、第1四分位数は25%、第2四分位数は50%(中央値)、第3四分位数は75%のデータのことを指します。
例えば、「1 2 3 4 5 6 7 8 9 10」の10個のデータについて考えます。
四分位なので、10個を4で割ります。
第1四分位数(Q1):10 / 4 = 2.5 → 今回は切り上げで3
第2四分位数(Q2):10 * 2 / 4 = 5
第3四分位数(Q3):10 * 3 / 4 = 7.5 → 今回は切り上げで8
Q1とQ3の差を取ります。
四分位範囲(IQR):8 - 3 = 5
外れ値の境界を下記のように設定します。
下側境界:Q1 - IQR * 1.5 = 3 - 7.5 = -4.5
上側境界:Q3 + IQR * 1.5 = 8 + 7.5 = 15.5
つまり、15.5より大きい数値、-4.5より小さい数値は、外れ値とみなす、ということになります。
実際のコードは下記になります。
import seaborn as sns
import pandas as pd
from numpy.random import randint
# グラフのサイズを指定
plt.figure(figsize=(20, 4))
# 正常データ、外れ値データを生成
correct_data = randint(0,100,100)
outer_data = randint(300,500,10)
# Pandas Seriesに変換
sample_data = pd.Series(np.concatenate([correct_data, outer_data]))
# 箱ひげ図を表示
plt.subplot(1, 4, 1)
sns.boxplot(data=sample_data)
# 第1四分位値
Q1 = sample_data.quantile(0.25)
# 第3四分位値
Q3 = sample_data.quantile(0.75)
# 第1四分位値 と 第3四分位値 の範囲
IQR = Q3 - Q1
# 下限値として、Q1 から 1.5 * IQRを引いたもの
LOWER_Q = Q1 - 1.5 * IQR
# 上限値として、Q3 に 1.5 * IQRをたしたもの
HIGHER_Q = Q3 + 1.5 * IQR
# 四分位数の観点から、外れ値を除外する
sample_data_iqr = sample_data[(LOWER_Q <= sample_data) & (sample_data <= HIGHER_Q)].dropna()
# 箱ひげ図を描画する
plt.subplot(1, 4, 2)
sns.boxplot(data=sample_data_iqr)
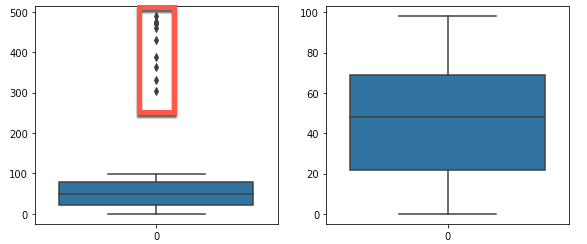
図示した結果が下記になります。
左側の生データの箱ひげ図では外れ値が含まれていますが、右側のグラフでは、四分位数から求めた境界で外れ値を除外することができていることが分かります。
2次元データの外れ値の検出
説明変数が1次元の場合は考えやすかったですが、2次元以上となる場合は複雑になります。
今回はIsolationForestと呼ばれる手法を使って、外れ値の検出を行います。
IsolationForestのメリットしては、教師なし学習が可能(正解ラベルが不要)という点です。
なので、比較的簡単に使うことができます。
今回は回帰データをダミーで作成します。
そのデータに外れ値を追加し、その外れ値を検出できるかどうかを確認します。
from sklearn.datasets import make_regression
import numpy as np
from matplotlib import pyplot as plt
from sklearn.ensemble import IsolationForest
# 回帰ダミーデータを作成する
X, Y, coef = make_regression(
random_state=12,
n_samples=100,
n_features=1,
n_informative=1,
noise=10.0,
bias=-0.0,
coef=True,
)
print("X =", X[:5])
print("Y =", Y[:5])
print("coef =", coef)
# 外れ値を追加する
X = np.concatenate([X, np.array([[2.2], [2.3], [2.4]])])
Y = np.append(Y, [2.2, 2.3, 2.4])
# X座標の値とY座標の値がばらばらなので、一つの変数にまとめる
X_train = np.concatenate([X, Y[:, np.newaxis]], 1)
# 生データすべてをプロットする
plt.figure(figsize=(20, 4))
plt.subplot(1, 4, 1)
plt.title("raw data")
plt.plot(X, Y, "bo")
# IsolationForestインスタンスを作成する
clf = IsolationForest(
contamination='auto', behaviour='new', max_features=2, random_state=42
)
# 学習用データを学習させる
clf.fit(X_train)
# 検証用データを分類する
y_pred = clf.predict(X_train)
# IsolationForest は 正常=1 異常=-1 として結果を返す
# 外れ値と判定したデータを赤色でプロットする
plt.subplot(1, 4, 2)
plt.title("outlier data(auto)")
plt.scatter(
X_train[y_pred == -1, 0],
X_train[y_pred == -1, 1],
c='r',
)
# 外れ値スコアを算出する
outlier_score = clf.decision_function(X_train)
# 外れ値スコアの閾値を設定する
THRETHOLD = -0.08
# 外れ値スコア以下のインデックスを取得する
predicted_outlier_index = np.where(outlier_score < THRETHOLD)
# 外れ値と判定したデータを緑色でプロットする
predicted_outlier = X_train[predicted_outlier_index]
plt.subplot(1, 4, 3)
plt.title("outlier data(manual)")
plt.scatter(
predicted_outlier[:, 0],
predicted_outlier[:, 1],
c='g',
)
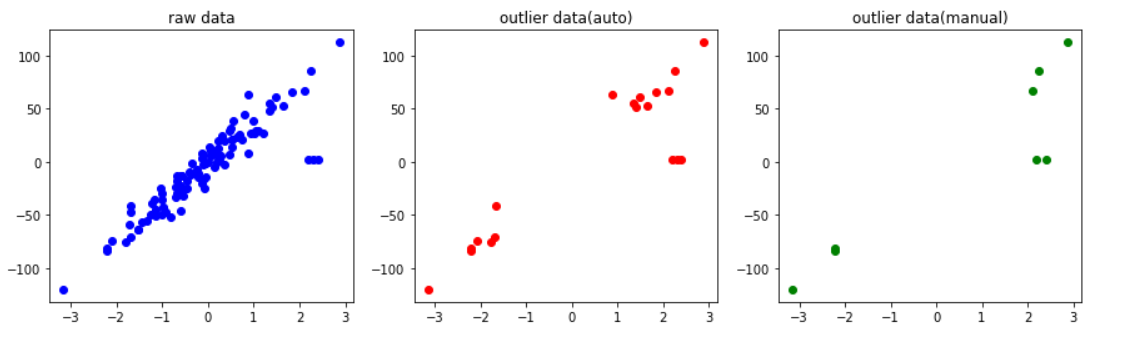
実行結果は、下記画像のようになります。
一番左の青色でプロットしたグラフは、生成したダミーデータを単純にプロットしたものになります。
真ん中の赤色でプロットしたグラフは、IsolationForestをデフォルト設定で使用し、外れ値を検出したものになります。
一番右の緑色でプロットしたグラフは、IsolationForestのdecision_function関数を使い出力した外れ値スコアを、こちらで設定した閾値で外れ値を検出しものになります。
ソースコード内のTHRETHOLDの値を変化させると、検出結果が変化することが分かると思います。
複数の説明変数が存在する場合、何を外れ値とするかは難しい問題かと思います。
IsolationForestを使うと、ゆるく外れ値を検出することができるので、手作業で外れ値を除くよりも、効率よく出来るのではないかと思います。
パラメーターをチューニングすれば、より厳しい条件で外れ値を除くことも可能です。(一番左の緑プロットのグラフ)
最後に
本当はコードの中身についてももう少し詳細に書きたかったのですが、間に合わず、、、
また、他の外れ値検出アルゴリズムも書きたかったのですが、それも(ry....
分かりにくい部分は今後修正するかもしれません。。。
2019年もみなさんいろいろとありがとうございました。
来年もよろしくお願いします!!(^▽^)