「乱数」数字が乱れた時、そこに魔力が生じ皆が魅了される。
あ。。
メリークリスマス!!
本日は、Cocone Advent Calendar 2023の24日目の記事になります!
担当するのは、cocone ONE株式会社のタカヤマです。よろしくお願いします!
ご存知の方は「あれ?」と思われたかもしれませんが、そうです。前回のアドベントカレンダーは、CTOとして参加させていただきましたが、夏頃に「新しいカタチで、ウェブ技術に特化した新チームの設立してほしい」と、指令が下りまして、「へい」と受けまして、cocone ONE株式会社にて新チームを立ち上げ、下半期はC++で実装されたプロダクトをRustで書き直し、 WebAssemblyを用いてウェブで動かすということをガッツリやっておりました。
バタバタCTOを倉さんと交代することになったのですが、倉さん始め、周りのエンジニアの皆さんにも協力して頂き、大きな問題もなく、スムーズに交代して頂いたことに感謝しております。
おかげさまで、Rust + WebAssemblyの知見も色々と溜まり、そちらのお話をしたい次第ではありますが、プロダクト自体がまだリリースされていないこともあって、またの機会とさせていただこうと思っております。
今年を振り返ってみますと、前半はFlutter、Flame、Dartに触れ、後半はRustとじっくり向き合った1年ではありました。
長年、OOP脳で生きて来た私にとっては、Rustの思考とガッツリ反対ということもあって、それはそれはぶつかったあった日々でもありました。プライベートでは扱って来たのですが、業務に取り入れるとなると考えることも多く、できることできないことを見極め日々奮闘しておりました。
Rustは今回のアドベントカレンダーでも大きな盛り上がりを見せ、とてもエンジニアに愛されている言語ではありますが、同時に難解プログラミング言語とも言われ、参入障壁が高いのでも有名です。C++エンジニアでも上手く書けなく挫折した。などの記事なども見受けられますが、一線を超えると心地よくなり、次第に「Rustしか勝たん」とも思うようになりました。
最近では、メモリ安全性、スレッド安全性の納得感も大きく、C++からRust移植を行っていくにつれ「C++緩くない?なぜこれでコンパイル通るの?」と感じ始め、メンバーとも話していたのですが、「C++はコンパイル通るけど実行時にコケる。Rustはコンパイル時にコケるが、コンパイル通ると安全に実行できる」と話してた事が、まさにそのとおりだなと思いました。
超個人的感想ではありますが、Rustは関数型プログラミング言語の影響も強いせいか、デフォルトでイミュータブルというスタンスを取られていますが、これが「お前らが変数を動的にバコバコ変更するからバグるんだよ。」と言われている感じがあり、意外と好きなところでもあったりします。確かに、全て定数だったらプログラム上のバグは発生しないだろうし、パフォーマンスも良い。
継承やシングルトンも「俺はそこまで面倒見ないからな。勝手にしな。」と突き放されている感じもあり、最近ではミュータブルに扱うことすら「すみません。」と思うようにもなり、借用の際も「すみませんがお借りします。」と一礼するようにもなりました。RCで共有頂く際も「恐れ入ります」と。(誇張しすぎました)
決して、他の言語がダメということではなく、Rustが本当によくできた言語で、他の言語と比べ一段上を行っているのだと思います。
あ。。今回はRustを布教する回ではなかったことを思い出しましたので、早速本題の波動関数崩壊アルゴリズムについて入っていきましょう。
(14秒経過)
波動関数崩壊アルゴリズムとは?
名前から凄そうな、Wave Function Collapse - 波動関数崩壊アルゴリズムってなんなのかですが、
Maxim Gumin氏が 2016年に 開発、公開した ランダム生成アルゴリズムとなっており、昔から存在するアルゴリズムと比較すると、比較的新しいアルゴリズムとなっています。(とはいえ7年経っておりますが。)
では、そのアルゴリズムは主にどういった風に活用するのかですが、まずはMaxim Gumin氏のGithub レポジトリを見てみましょう。
見た感じ、「タイルマップのイメージ」を入力データとして「膨大にあるパターンからランダムに選択して生成されたグラフィック」が出力されているのが確認できます。
と聞くと、ディープラーニングなどニューラルネットワークをイメージされるところもありますが、そういった機械学習とは異なり、シンプル且つ容易に活用できるアルゴリズムとなっております。
実際にどの様なところで利用されるかですが、「ランダムに生成」となると、ゲーム内で利用されるシーンが多く、ローグライクゲームのダンジョンやボクセルゲームのワールドマップなど多種多様で、生成方法のアルゴリズム自体もゲームによっても異なります。
簡易で有名なアルゴリズムとして棒倒し法などがありますが、波動関数崩壊アルゴリズムはそれら同様に活用できるアルゴリズムとなっております。
ゲームによって、レベルジェネレーターが存在し、魅力のあるマップを生成するためノイズ関数などを用いて生成するのですが、ダンジョンの部屋によっては、大きな部屋の中心に特定のオブジェクトが存在する必要があるとか、水が溶岩やその他のものと隣接してはいけないとか、マップ生成における制約を与えより細かく制御し、特定のオブジェクトが配置される場所に制限を加えてレベルを生成したい時にWave Function Collapse (以下 WFCとする)は有用とされています。
レポジトリのサンプルでもあるように、RPGであるマップを描くことも可能です。
JSで活用したサンプル
アルゴリズム自体、C#で記述されていることもあって、Unity用のプラグインが作成されたり、Unityで作成されたゲームで活用されているのを多く見かけますが、Unityだけに限らず、Unreal Engine、PICO-8といった様々なゲームエンジンにも用いられ、2Dゲームのみならず3Dゲームにも応用でき、実際にレポジトリのサンプル画像にも掲載されている迷路や、SteamなどのプラットフォームでリリースされているゲームのTownscaperなどにも適応されており、言語、ゲームエンジン、ジャンルを問わない故に活用実績も多く範囲も幅広いです。
Tile ModelとOverlapping Model
といったところで、WFCの概要は分かったところで中身について見ていきましょう。
WFCには大きく2つの生成モデルがあります。Tile ModelとOverlapping Modelです。
Overlapping Model
入力画像から取得した小さな部分の集合を使用して、出力画像を生成。セグメントがどのように重なり合うかに重きを置いている。基本的に、このモデルは入力画像内で見つかるすべての可能な N×Nピクセルのパターンを分析し、これらのパターンの重なりを考慮して新しい大きな画像を生成。
特徴:
- 詳細な出力: 元の画像の微細な特徴をキャプチャし、出力に反映させる。
- 非周期的なテクスチャの生成: 入力画像から繰り返しのないパターンを生成に適している。
- 複雑な構成: 入力画像の様々な部分からの情報を組み合わせることで、より複雑で詳細な出力を生成可。
Tile Model
予め定義されたセットのタイルを使用して画像を生成。これらのタイルは、特定のルールに基づいて隣接することができ、連続した画像が形成される。タイルは通常、辺や角が他のタイルと一致するように設計されており、それらが合わさって一貫性のある全体像を作成。
特徴:
- 規則性と一貫性: タイルが持つ明確な規則と一貫性によって、均一なパターンや構造を生成するのに適している。
- ゲームデザインでの応用: タイルベースのゲームデザインに特に適しており、マップやレベルの自動生成に用いられる。
- シンプルな設計: タイルモデルは、Overlappingモデルに比べて実装が比較的シンプルで、特定の種類のタイルに基づいてパターンを作成。
ということで、今回はOverlappingモデルよりシンプルなTile Modelに注目していきたいと思います。
Entropy (エントロピー)
では、中身を見ていきたいのですが、その前に、そもそも、Wave Function Collapse - 波動関数崩壊アルゴリズムっていう名前の由来は?と思う方も少なくないかと思いますが、こちら量子力学が元になっているようで、量子力学での名称は「波動関数の収縮または波動関数の崩壊」となっています。
用語自体は量子力学に由来しているみたいですが、その波動関数の崩壊とはどういう事か考えていくのですが、ここで出てくるの大事な要素が「Entropy (エントロピー)」となります。
wikipediaを見てみることにしましょう。
エントロピー(英: entropy)は、熱力学および統計力学において定義される示量性の状態量である。
熱力学において断熱条件下での不可逆性を表す指標として導入され、統計力学において系の微視的な「乱雑さ」を表す物理量という意味付けがなされた。
統計力学での結果から、系から得られる情報に関係があることが指摘され、情報理論にも応用されるようになった。
物理学者のエドウィン・ジェインズ(英語版)のようにむしろ物理学におけるエントロピーを情報理論の一応用とみなすべきだと主張する者もいる。
はい。よくわかりませんね。w
今回のWFCでは、後半の情報理論の方の応用に該当し、ある事象が起きた際、それがどれほど起こりにくいかを表す尺度となります。
例えば散歩していて、ありふれた出来事として「風の音」が起きた事を知ってもそれは大した「情報」にはならないが、「曲の演奏」が聞こえてくれば珍しい出来事としてより多くの「情報」を含んでいると考えられます。
つまり、情報量はその出来事が本質的にどの程度の情報を持つかの尺度としてみなされます。
その「Entropy (エントロピー)」と情報理論を用いて、数年前に流行ったゲーム「Wordle」を、より少ない試行回数で当てる方法の解説動画が面白かったのですが、こちらまで見ていくと5分を過ぎてしますので興味ある方で観ていただければと思います。
Solving Wordle using information theory
(1分4秒経過)
数独 (sudoku)
今回のWFCで用いられる概念として、数独 (sudoku)があります。
数独(ナンバープレイス、通称ナンプレ)は、始めるとやめられないですよね。コンビニの雑誌コーナーとかでも販売されていて、昔はよく朝になるまでやっていたり、わざわざゲームソフトとしてリリースしている数独を購入したりとハマっていた時期もありました。
と、話は逸れてしまいましたが、Entropy (エントロピー)」に関しては数独 (sudoku)が理解しやすいのでそれに置き換えてみていきましょう。
まず、数独 (sudoku)のルールとして、9x9のグリッドに3x3の小さなボックスと呼ばれる9つのセクションに分割されていて、行、列、ボックスに1から9までの数字が一度ずつ現れるルールとなっています。
もし、セルすべて空白の場合、セルには1〜9の数字が埋められています。
この時の平均エントロピーは9となります。

以下のセルに5が入った場合、行、列、ボックスに影響しエントロピーが減少します。

同じ行、列、またはボックスにある他のセルには5が含まれないことがわかります。
その情報より影響を受けるセルに伝播し、重ね合わることにより、5の数字を削除することができます。変化したセルは8つの数字の可能性を持った状態となります。
また、ここに9の数字が入ったとすると、先程同様に、行、列、ボックスに影響しエントロピーが減少します。

この様に、数字が確定すると、他のセルにその状態が伝播し折りたためられていきます。
5や9などを選択した例の様にその状態が1つの選択肢に確定すると、隣接するセルのエントロピーが減少し、そこから推測を開始します。
数独を解くまで推測、崩壊、推測、崩壊…が繰り返されていきます。
この様に波動関数崩壊アルゴリズム内に存在するプロセスと、数独を解くプロセスは同じで、エントロピーが少ないタイル、つまりその中に入る可能性のある数値が最も少ないタイルを探していきます。

すべての可能な状態から1つに崩壊させること、システムの単一変数から全てのエントロピーを削除する事を波動関数の崩壊と言います。

(1分37秒経過)
隣接性を持ったソケットシステム
数独のプロセスを参考にWFCのプロセスを見えきましたが、では実際にタイルマップがどの様に確定していくかを見ていきたいと思います。
特定のセルが折りたたまれ、そのセルが確定した場合隣接するセルのエントロピーが減少していく。ということは、つまり隣接しているセルの選択肢が接続可能なセルに絞られていくこととなります。
上記のプロセスの特定のセルが1つの選択肢に確定、隣接するセルのエントロピーが減少していく様子がタイルマップを用いて視覚的に理解しやすく試せるデモがこちらにあります。

タイルマップをクリックで選択すると、隣接するセルの情報も減少し選択肢も絞れていき、タイルマップを確定してく様子が確認できるかと思います。
もっとシンプルなタイルマップに置き換え見ていきましょう。以下の様なタイルマップ画像を用いてグラフィックを生成するとします。
単色で塗りつぶされたBlank画像、上下左右に回転されたT画像。各タイルでコネクトされる関係性をタイルのエッジに接続可能を示す何らかの識別子を持たせます。その識別子を0、1と数字のソケットとして持った場合、以下の様になるかと思います。
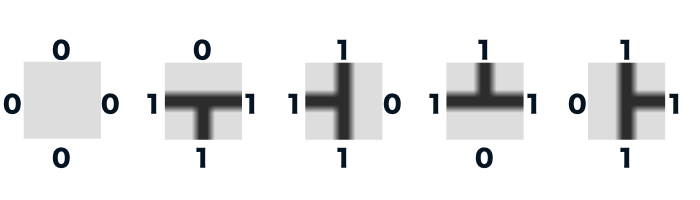
単色で塗りつぶされたBlank画像の各エッジのソケットは全て0。T画像の持つソケットは0と1で、0は0とコネクトし、1は1とコネクトし、0と1のコネクトは無効となります。用意したBlank画像とT画像の隣接関係は以下の様になるかと思います。
もちろん、0と1のみならず、2や3と増やすことも可能で、制約の与え方も様々です。
なにより重要なポイントは、セル境界で一致しないタイルの隣接関係を無効にする。というところになります。
Oskar Stal Berg氏の有名なデモでは、タイルのエッジに沿った 3つの固定点のピクセルによってソケットは決定され、隣接するタイルの色が3つの点で一致するかどうかでを検証し隣接関係の無効、有効化を行っています。
拡大すると、各エッジに3つの色情報を持っているのが確認できます。
この様に、セルの各エッジのソケットを1つではなく、3つにすることによってより詳細な隣接関係の制約を持たせることができ、複雑なグラフィックな色彩に沿った滑らかなグラフィックも生成することが可能となっております。

今回は、色情報をベースとし、色情報ではなくA、B、Cとアルファベットで識別することにします。
結局のところ、タイルモデルにおける隣接関係で重要なポイントは、
どのモジュールがどのモジュールとスロットできるか、できないか、また、それらはどの方向が有効か無効か。 が、大事といえます。
(2分11秒経過)
WFCをRustで実装
それでは、仕様も出揃ったところなので実装に入って行きたいと思います。
今回は、言語にはRust、描画にはSDLを用いて実装を行います。
環境
- macOS Sonoma 14.1.1
- rustc 1.73.0
crates
- sdl2 0.36.0
- tokio 1
- serde 1.0
- serde_json 1.0
- num 0.4.1
- rand 0.8.5
WFCの大きな流れとしては、以下の初期設定を行います。
- タイルの画像、制約情報を入力データとする
- グリッド内にセルとして全ての可能性として保持
WFC実行フローとして、
- エントロピーの低いセルを優先するため、グループ化して取得
- タイルをランダムに選択、セルを1つの選択肢に確定。
- 隣接するセルのソケットを評価し、各セルのエントロピーを減少
- 伝播し終わると再度処理を実行
となり、全てのセルが崩壊、つまり1つの選択肢に確定となるとWFCの処理は終了となります。
タイルの画像、制約情報を入力データとする
まず、タイルの画像と制約情報を持ったデータの作成を行います。
JSONフォーマットで、用意します。スキーマの詳細は以下の通り。
- src: 画像のパス
- edges: 各エッジのソケット条件
- isRotate: 回転可能か否か
"tileList": [
{
"src": "simple/blank.png",
"edges": ["AAA", "AAA", "AAA", "AAA"],
"isRotate": false
},
{
"src": "simple/t.png",
"edges": ["AAA", "ABA", "ABA", "ABA"],
"isRotate": true
}]
}
edgesは、上、右、下、左の順番で記述しています。
上部の端は、「左、中、右」、右部の端は、「上、中、下」、下部の端は、「右、中、左」、左部の端は、「下、中、上」といった順番で形でedgesに配列で記述していきます。
isRotateに関しては、「回転して利用できるか否か」になります。
単色のblankは回転して利用しても向き、形が何も変わりませんので回転する必要がなく、逆にT画像に関しては全ての向きの画像分の種類の用意の必要がなく、1つを時計回りに90度ずつ3回回転させて流用することで、1枚の画像で4パターン生成することが可能です。
なので、以下のパターンを網羅するには、2枚の画像があればカバーできますので2枚の画像で回転を含めた5パターンのタイルマップを用意することになります。
Grid、Tile classの作成
今回のディレクトリ構造は以下の様にしました。
ファイル構成
src/
├── constants
│ └── defines.rs
├── constants.rs
├── core
│ ├── cell.rs
│ ├── tile.rs
│ └── wfc.rs
├── core.rs
├── main.rs
├── utility
│ ├── error.rs
│ └── utility.rs
└── utility.rs
各ディレクトリの概要は、
- constants: 定数、コンフィグなど定義ファイル
- core: cell、tilesのstruct、WFCメインの処理
- utility: その他の処理
となっております。
それでは、実ソースの方を見ていきます。
まず、今回はSDLを用いているのもあり、main関数でsdl2の初期化を行い、(sdl2の初期化は割愛させていただきます) Cellのベクターを保持するgridと、Tileベクターを保持するtilesを用意します。
gridはタイルマップ全体となっており、タイルのマス分Cellが格納されます。
また、tilesは先程JSONファイルで用意したデータを元に生成されたTile classを格納することになります。
async fn main() -> Result<(), MyError> {
let sdl_context = sdl2::init()?;
let mut canvas = sdl_init(&sdl_context)?;
let texture_creator = canvas.texture_creator();
let tiles = init_tiles(&texture_creator).await?;
let mut grid: Vec<Cell> = init_grid(tiles.len());
...
Tile structは以下の様になります。
JSONファイルで定義したedges、isRotateを保持し、imageのpathを元にtextureを生成します。また、回転が必要であればangleの値も計算。
その他に、コネクトできるTileのindexを保持する配列、 up、right、down、leftを intのListで用意します。
pub struct Tile<'a> {
pub texture: Rc<Texture<'a>>,
pub edges: Vec<String>,
pub angle: f64,
pub is_rotate: bool,
pub up: Vec<usize>,
pub right: Vec<usize>,
pub down: Vec<usize>,
pub left: Vec<usize>,
}
init_tiles関数で、canvas.texture_creatorを引数に、JSONデータよりTileのインスタンスを生成します。
async fn init_tiles(texture_creator: &TextureCreator<WindowContext>) -> Result<Vec<Tile>, MyError> {
let mut tiles = create_tiles_from_json(&texture_creator, JSON_FILE_NAME).await?;
create_rotate_tiles(&mut tiles);
generating_adjacency_rules(&mut tiles);
Ok(tiles)
}
pub async fn create_tiles_from_json<'a>(
texture_creator: &'a TextureCreator<WindowContext>,
file_name: &str,
) -> Result<Vec<Tile<'a>>, MyError> {
let tile_list_data = load_json_data(file_name).await?;
let mut tiles = Vec::new();
for tile_data in tile_list_data.tile_list {
tiles.push(Tile::load(
texture_creator,
tile_data.src,
tile_data.edges,
tile_data.is_rotate,
)?);
}
Ok(tiles)
}
isRotateのフラグが立ったものに関しては回転バージョンのTileインスタンスを生成します。
90度、180度、270度の回転の3種類を追加するので、1/2π * n が行えるようにfor文は1始まりとします。
fn create_rotate_tiles(tiles: &mut Vec<Tile>) {
let mut new_tiles = Vec::new();
for tile in tiles.iter() {
if tile.is_rotate {
for j in 1..4 {
new_tiles.push(tile.rotate(j));
}
}
}
tiles.extend(new_tiles);
}
こちらの処理を終え、全てのTileインスタンスの生成は行えました。
各タイルの隣接性を作成
generating_adjacency_rules関数にて、全タイルの隣接関係の評価を行いそのタイルは 上、右、下、左にどのタイルとコネクト可能かを調べます。
fn generating_adjacency_rules(tiles: &mut [Tile]) {
let tile_edges: Vec<_> = tiles.iter().map(|tile| tile.edges.clone()).collect();
for (index, tile) in tiles.iter_mut().enumerate() {
tile.analyze(&tile_edges, index);
}
}
自分自身のedgesの0番目は上なので、他のタイルとは、下部にあたるedgesの2番目と接続となるので、edges[0]とedges[2]を評価します。
pub fn analyze(&mut self, tile_edges: &[Vec<String>], current_index: usize) {
for (index, edges) in tile_edges.iter().enumerate() {
if index == current_index {
continue;
}
// UP
if compare_edge(&edges[2], &self.edges[0]) {
self.up.push(index);
}
// RIGHT
if compare_edge(&edges[3], &self.edges[1]) {
self.right.push(index);
}
// DOWN
if compare_edge(&edges[0], &self.edges[2]) {
self.down.push(index);
}
// LEFT
if compare_edge(&edges[1], &self.edges[3]) {
self.left.push(index);
}
}
}
その際、edgesに格納されたままだと評価できないので、文字列を逆にする処理を入れています。
pub fn reverse_string(s: &str) -> String {
s.chars().rev().collect()
}
pub fn compare_edge(a: &str, b: &str) -> bool {
a == reverse_string(b)
}
例えば、以下の様なタイルチップがあった場合、
※1 このタイルが保持するedgesは[”AAB”, ”BBB”, ”BAA”, ”ACA”]となります。
※2 絵から、同じタイルの上部と下部でコネクトできそうなのがわかります。
※3 実際に上部と下部は「AAB」と「AAB」
※4 しかしながら下部で保持しているedgesは「BAA」となるので片方文字列を反転し評価する必要があります。
左右の評価も同様となります。
Grid 作成
最初に記述した、「グリッド内にセルとして全ての可能性として保持」のフローとなります。
まず、Grid全体の大きさを決めたいので定数DIM(dimension)を定義し、こちらでグリッド全体の大きさを決定します。
DIM * DIM(縦 * 横)で、Grid作成と同時に Cellを作成します。
pub const DIM: usize = 15;
from_valueファクトリーメソッドで、Cellのインスタンスを生成します。
fn init_grid(length: usize) -> Vec<Cell> {
(0..DIM * DIM)
.map(|_index| Cell::from_value(length))
.collect()
}
CellのsocketsはTileのindexとなります。つまり、初期状態は「全ての可能性を持った」状態となり、エントロピーも最大のTileの全体数となります。
pub struct Cell {
pub collapsed: bool,
pub sockets: Vec<usize>,
}
impl Cell {
pub fn from_value(value: usize) -> Cell {
Cell {
collapsed: false,
sockets: (0..value).collect(),
}
}
pub fn from_list(value: Vec<usize>) -> Cell {
Cell {
collapsed: false,
sockets: value,
}
}
}
(3分21秒経過)
Wave Function Collapse - 波動関数崩壊アルゴリズム メインフロー
準備は整いましたので、ここからWave Function Collapse - 波動関数崩壊アルゴリズム のメインフローとなります。
fn main_loop(grid: &mut Vec<Cell>, tiles: &[Tile]) {
let mut low_entropy_grid = pick_cell_with_least_entropy(grid);
if low_entropy_grid.is_empty() {
return;
}
if !random_selection_of_sockets(&mut low_entropy_grid) {
*grid = init_grid(tiles.len());
return;
}
wave_collapse(grid, tiles);
}
再度流れを振り返ると、
-
エントロピーの低いセルを優先するため、グループ化して取得
- pick_cell_with_least_entropy
-
タイルをランダムに選択、セルを1つの選択肢に確定
- random_selection_of_sockets
-
隣接するセルのソケットを評価し、各セルのエントロピーを減少
- wave_collapse
となります。
pick_cell_with_least_entropy関数
「エントロピーの低いセルを優先するため、グループ化して取得」を行っていきます。
まず、現在のgridの状態をシャローコピーしたいので、grid_copy変数に格納します。
そのcell自身がcollapsed、つまりセルが確定しているのであれば無視し、セルが確定していないものでフィルタリングします。
その後、セルのsocketsの数が少ない順、つまりエントロピーの低い順にソートを行います。
通常であればきちんと計算や重みつけなども考慮しますが、今回は単純に低エントロピーはsocketsの少ない順とします。
pub fn pick_cell_with_least_entropy(grid: &mut Vec<Cell>) -> Vec<&mut Cell> {
let mut grid_copy: Vec<&mut Cell> = Vec::new();
for cell in grid.iter_mut() {
if !cell.collapsed {
grid_copy.push(cell);
}
}
if grid_copy.is_empty() {
return Vec::new();
}
grid_copy.sort_by_key(|cell| cell.sockets.len());
let len = grid_copy[0].sockets.len();
let stop_index = grid_copy
.iter()
.position(|cell| cell.sockets.len() > len)
.unwrap_or(grid_copy.len());
grid_copy.truncate(stop_index);
grid_copy
}
その後、最小エントロピーのグループ化として、最初のcellのsocketsの数を調べそれを超える場合は排除します。
つまり、[1,2],[1,2],[1,2],[1,2,3] となった時点でそのindexを取得しtruncateでカットを行います。
random_selection_of_sockets関数
「タイルをランダムに選択、セルを1つの選択肢に確定」を行っていきます。
ここでは、見つからない場合の考慮も行います。
「見つからない場合」とは、制約ルールによってはコネクトできずパターンがなくなる事も発生することがあります。その際、再度最初からやり直すため Gridを初期化します。
if !random_selection_of_sockets(&mut low_entropy_grid) {
*grid = init_grid(tiles.len());
return;
}
random_selection_of_sockets関数は、最小エントロピーのグループからcellをランダムに選択し、collapsedをtrueにして確定フラグを立てます。そのcellのsocketsからどのタイルにするかもランダム選択し、表示するタイルを確定させます。
pub fn random_selection_of_sockets(grid_target: &mut Vec<&mut Cell>) -> bool {
let mut rng = rand::thread_rng();
if let Some(cell) = grid_target.choose_mut(&mut rng) {
(*cell).collapsed = true;
if cell.sockets.is_empty() {
return false;
}
if let Some(&pick) = cell.sockets.choose(&mut rng) {
cell.sockets = vec![pick];
true
} else {
false
}
} else {
false
}
}
(4分9秒経過)
wave_collapse関数
いよいよ、WFCのコアの部分に迫ってきました。
最後のフロー「隣接するセルのソケットを評価し、各セルのエントロピーを減少」となります。
改めて、ここで行っている事は、グリッド全体の左端から上下左右のセルのsockets、すなわちコネクトできるタイルのindexを見て、自分自身のcellの状態を変化させることです。
各セルの状態は、配置可能なtileを絞られることになるのですが、それがエントロピーの減少となります。
wave_collapseには、gridとtilesを引数に渡します。
wave_collapse(grid, tiles);
それでは、中身をみていきましょう。
pub fn wave_collapse(grid: &mut Vec<Cell>, tiles: &[Tile]) {
let mut next_grid: Vec<Option<Cell>> = vec![None; DIM * DIM];
for j in 0..DIM {
for i in 0..DIM {
let index = i + j * DIM;
if grid[index].collapsed {
next_grid[index] = Some(grid[index].clone());
} else {
let mut sockets: Vec<usize> = (0..tiles.len()).collect();
// Look up
if j > 0 {
cell_collapse(&mut grid[i + (j - 1) * DIM], "down", &mut sockets, tiles);
}
// Look right
if i < DIM - 1 {
cell_collapse(&mut grid[i + 1 + j * DIM], "left", &mut sockets, tiles);
}
// Look down
if j < DIM - 1 {
cell_collapse(&mut grid[i + (j + 1) * DIM], "up", &mut sockets, tiles);
}
// Look left
if i > 0 {
cell_collapse(&mut grid[i - 1 + j * DIM], "right", &mut sockets, tiles);
}
next_grid[index] = Some(Cell::from_list(sockets));
}
}
}
grid.clear();
grid.extend(next_grid.into_iter().filter_map(|cell| cell));
}
まず、次のGridの状態に書き換え用の空のベクターnext_gridをグリッド範囲分の幅で用意。
let mut next_grid: Vec<Option<Cell>> = vec![None; DIM * DIM];
チェックするセルの順番ですが、グリッドの左端から確認していくこととなります。
for j in 0..DIM {
for i in 0..DIM {
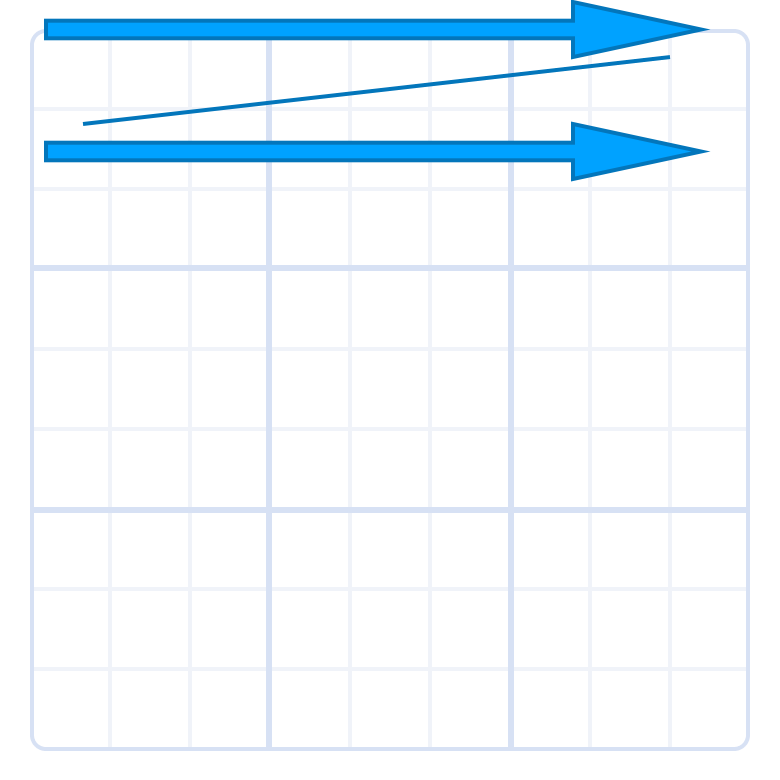
もし、対象のセルが確定していればそのセルはそのまま次のグリッドの状態に渡します。
if grid[index].collapsed {
next_grid[index] = Some(grid[index].clone());
}
配置できるsockets(エントロピー)を、まずは全可能性を持った状態で初期化を行います。tilesの数だけindexを持ったベクターを作成し、そこから絞っていきます。
let mut sockets: Vec<usize> = (0..tiles.len()).collect();
続いて、今のセルの上、右、下、左の順番で隣合うセルをチェックしていきます。
if j > 0 {
cell_collapse(&mut grid[i + (j - 1) * DIM], "down", &mut sockets, tiles);
}
jは行となり、j= 0は一番上の行となるので、最初の行に関してはこちらはスキップされます。まず一番最初に行われるセルは左上端のセルとなり、隣り合う右のセルをチェックすることになります。

cell_collapse関数で実際にcellの折りたたみを行うこととなります。
右のセルをチェックする場合、grid[i + 1 + j * DIM]で右側のcellを参照します。
自分自身に対して右側なので、そのセルは左側にコネクト可能なタイルを検証することになります。
cell_collapse(&mut grid[i + 1 + j * DIM], "left", &mut sockets, tiles);
...
fn cell_collapse(cell: &Cell, direction: &str, sockets: &mut Vec<usize>, tiles: &[Tile]) {
let valid_sockets = get_valid_sockets(cell, direction, tiles);
check_valid(sockets, &valid_sockets);
}
cell_collapse関数で行っていることは、get_valid_socketsでコネクトsockets(コネクト可能なタイルインデックス)を取得し、check_validで比較し存在しなければ引数で渡されたsocketsのindexは削除。となります。
get_valid_sockets関数
fn get_valid_sockets(cell: &Cell, direction: &str, tiles: &[Tile]) -> Vec<usize> {
let mut valid_sockets = Vec::new();
for &socket in &cell.sockets {
let valid = &tiles[socket].valid(direction);
valid_sockets.extend(valid);
}
valid_sockets
}
cellはチェック対象(流れ的に 最初は右側)のセルとなり、そのセルの持つsockets(タイルインデックス)分、tileのvalidメソッドで確認していきます。
右側のセルの場合は “left”となり、tileインスタンス生成時設定したleft、つまり左側にコネクト可能な tileのindexの配列を返却します。
pub fn valid(&self, direction: &str) -> Vec<usize> {
match direction {
"up" => self.up.clone(),
"right" => self.right.clone(),
"down" => self.down.clone(),
"left" => self.left.clone(),
_ => Vec::new(),
}
}
チェック対象のcellのsockets(tile)の数だけ、コネクト可能な tileのindexを追加します。
valid_sockets.extend(valid);
最後に、check_validで先程作成したコネクト可能なtileのindex全てが追加されたvalid_socketsと、チェック時に作成したsocketsを比較し、存在しなければ削除します。
fn check_valid(sockets: &mut Vec<usize>, valid_sockets: &[usize]) {
sockets.retain(|socket| valid_sockets.contains(socket));
}
ここで、エントロピーの減少が発生したことになります。
上下左右チェックし、一つでも置けない可能性があるのであれば崩壊することとなります。
※ 一方が「2, 4」しかコネクトの可能性がない例

この様に、自分の上下左右のセルをチェックし、そのセルの影響で自分自身のエントロピーが減少し、伝播していくことが波動関数の崩壊となります。
グリッド全てのセルのチェックが終わると、grid自体を崩壊後のグリッドに置き換えます。
grid.clear();
grid.extend(next_grid.into_iter().filter_map(|cell| cell));
この様に、wave_collapse関数では隣り合うセルの状態を確認し、セルの持つsocketsの可能性を絞って行くことでエントロピー減少させて、再び低エントロピーからランダムに選択しタイルを確定。また、wave_collapse関数で隣り合うセルのチェック....。
と繰り返すことで、崩壊は伝播していきます。
描画
最後に描画処理となります。
fn draw(canvas: &mut Canvas<Window>, grid: &[Cell], tiles: &[Tile]) {
let w = GAME_WIDTH / DIM as u32;
let h = GAME_HEIGHT / DIM as u32;
for j in 0..DIM {
for i in 0..DIM {
let index = i + j * DIM;
let cell = &grid[index];
if cell.collapsed {
let tile_index = cell.sockets[0];
let tile = &tiles[tile_index];
tile.render(
canvas,
(i as u32 * w).try_into().unwrap(),
(j as u32 * h).try_into().unwrap(),
w,
h,
);
}
}
}
}
loopで、draw関数実行し、(fps挟んでないのでCPUを占有しちゃうかも) cell.collapsedの状態を監視し描画するかどうかを振り分けています。
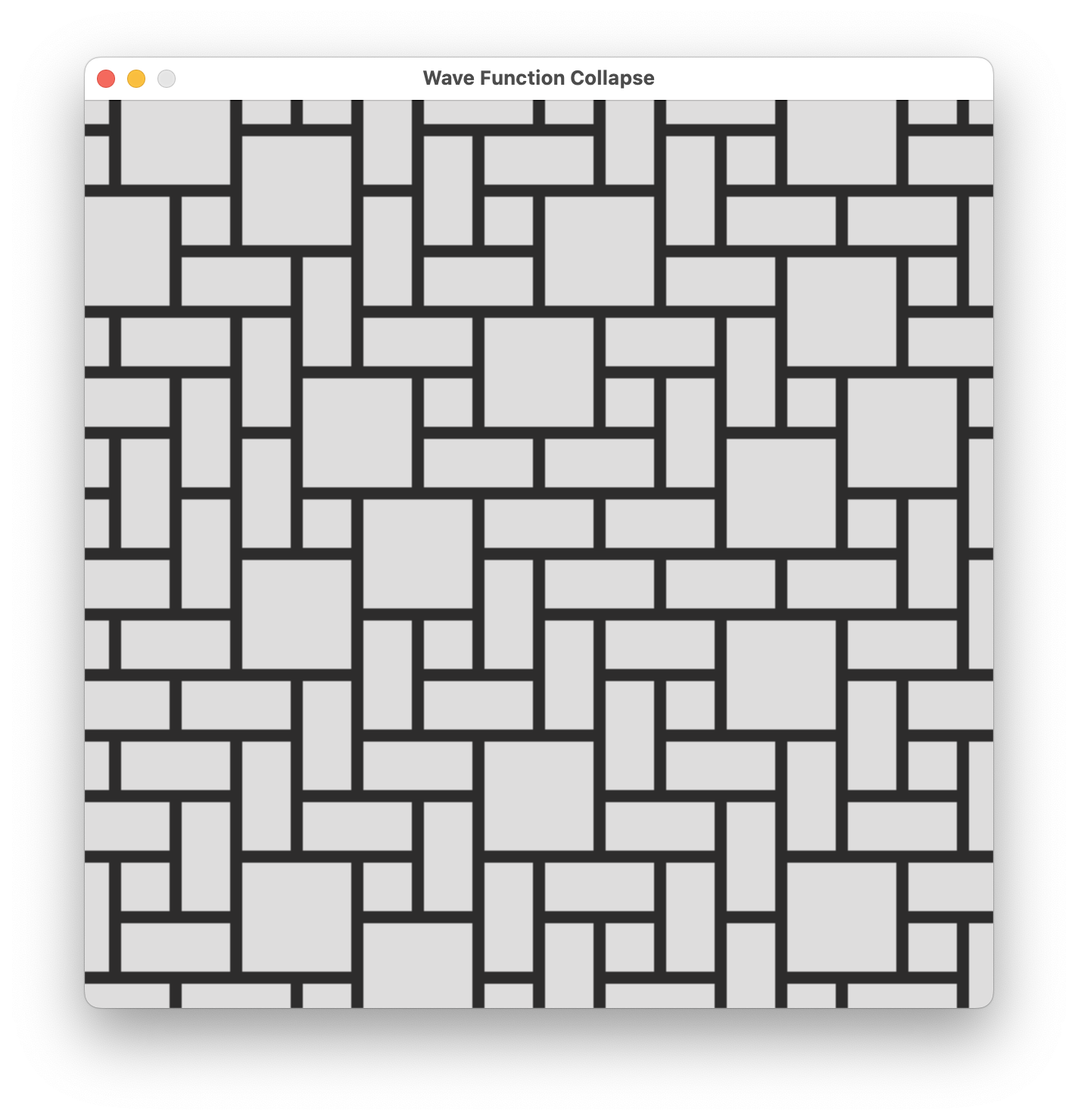
それでは実行してみましょう。
はい。
いい感じにできましたね。
その他のサンプルも試してみましょう。

おお。いい感じですね。

いい感じだがちょっと調整必要。

こちらは部屋の図面ぽいですね。
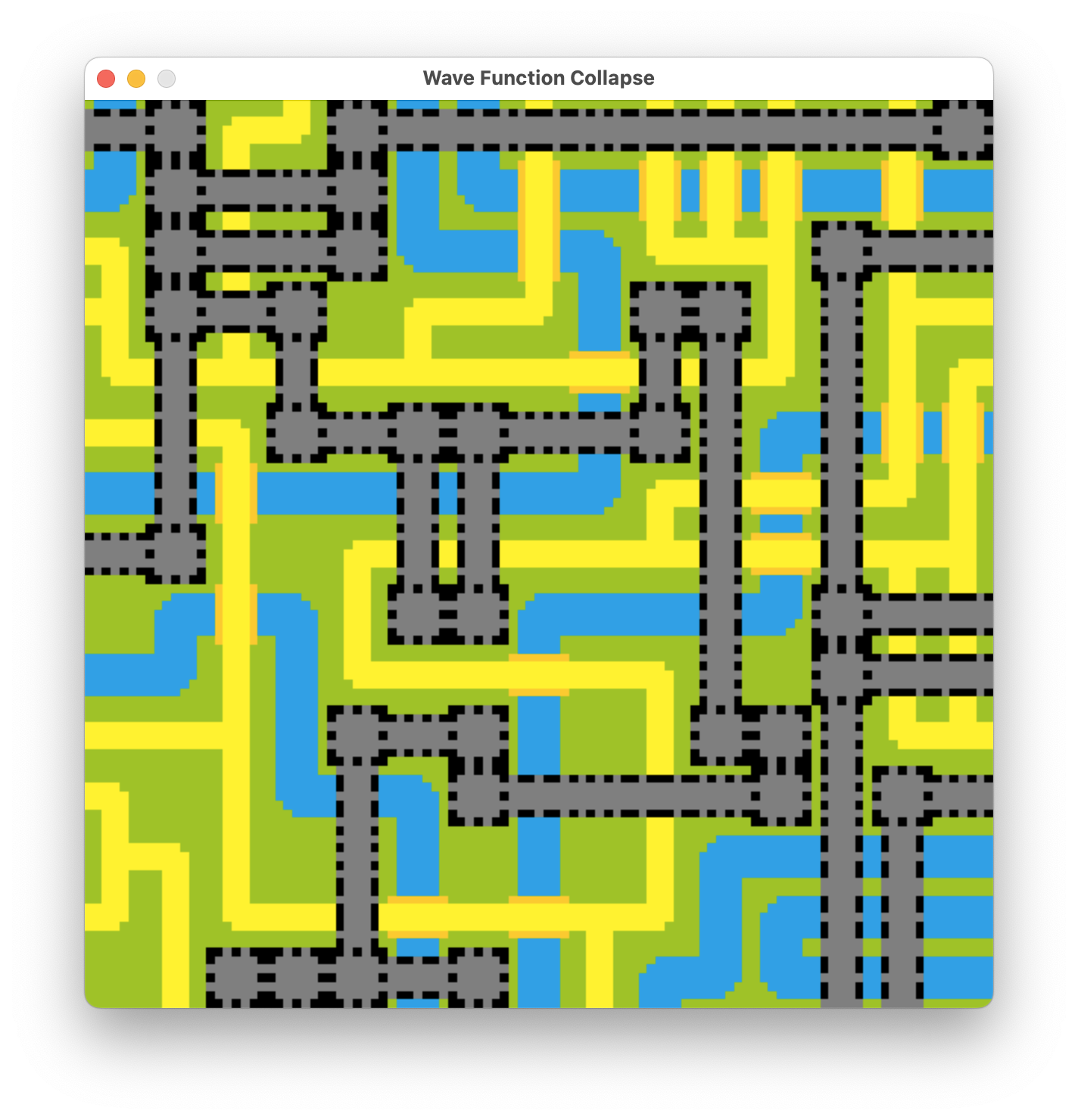
いい感じですが、ちょっと調整が必要そうですね。

これは、あっているのか。違いますよね。
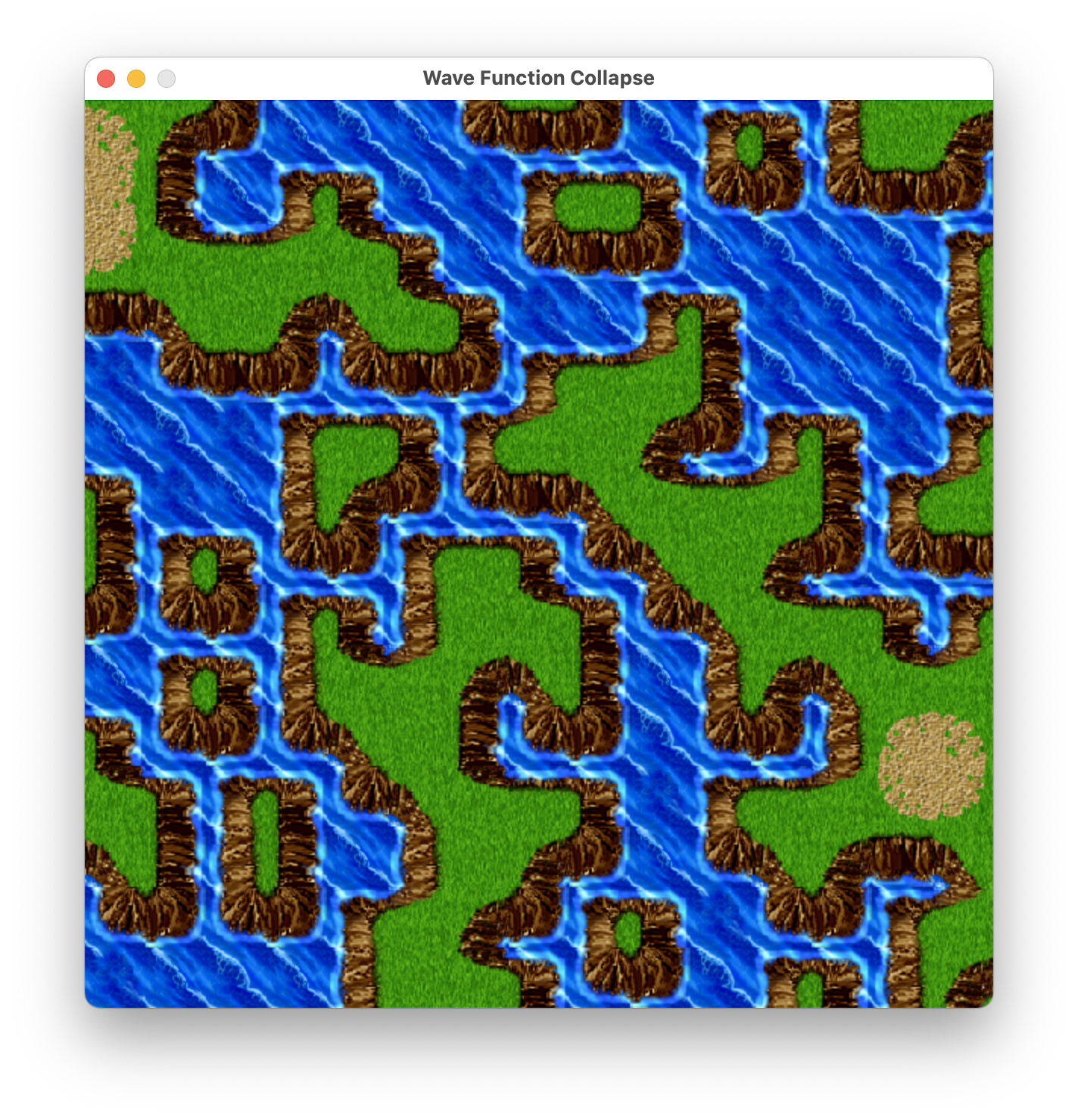
RPGマップも良い感じではありますが、調整が必要そう。
と、意図した通りに表示したのと、ちょっと違かったのと、制約の調整が必要そうなものもありましたが、取り敢えずは完成。制約の付け方で表示も異ってくるのも確認できました。
今回作成したソースはこちらになります。
それはそうと、実は、Flutter、Flameを用いても実装していましたが、やっぱRust実装のほうが起動、実行ともにパフォーマンスよく快適でした。しかしながら、Flutterの方が意図的な表示なっていたりして、Rust側の見直しが必要そう。
(5分12秒経過)
最後に
という訳で、今回はWave Function Collapse - 波動関数崩壊アルゴリズムのTile Modelを実装してみました。
5分を大幅に過ぎてしまうんじゃないかと思っていましたが、5分12秒となんとか5分台に収められて良かったです。
いやぁ。いかがだったでしょうか。この冬休みは、Overlapping Modelも含めトライしてみてはいかがでしょうか。
最近、ハマっているゲームは今更ながらかもですが「Forager」になります。
2Dアクションクラフトゲームということで、2Dアクションやクラフトゲームやドット絵好きの私としては、盆と正月が一緒に来たような感覚です。興味のある方はよろしかったらどうそ。
明日の最終日は@nihonsyuさんの記事で締めていただきます!
引き続き、最後までCocone Advent Calendar 2023をよろしくお願いいたします!
参考文献












