以前の記事で、組合せ最適化問題を深層強化学習を用いて解く一例を、関連論文に沿ってご紹介しました(巡回セールスマン問題を深層強化学習で解いてみる)。今回もある種の組合せ最適化問題と考えられる、ルービックキューブを深層強化学習を用いて解く試みをご紹介しようと思います。
ルービックキューブと強化学習
皆さんご存知のルービックキューブは、各面を次々に回転させることによって解の状態を得るパズルゲームです。小さい頃に慣れ親しんだ方も多いと思いますが、私も学生時代に置換群に関連して少々調べたことがあり、思い入れのあるパズルでした1。このルービックキューブは、ある任意の状態から解にたどり着くまでの最適な回転手続きの組合せを見つける組合せ最適化問題として考えることもできます。


可能な組合せ数が爆発することから、ナイーブに全探索するのが現実的でないことは以前の巡回セールスマン問題と同様です。この様な問題に対して、様々なヒューリスティクな解法が提案されているのも同様で、群論を基礎にしたKociemba's algorithmや、探索ベースのKorf's algorithmなどが代表的なアルゴリズムになっているようです。
この問題に対して、深層強化学習を用いて妥当な求解アルゴリズムをデータから構築するのが今回ご紹介する試みです。
以前の記事でも記載した様に、強化学習や機械学習の手法を用いることで、既存の手法が持つ長所、短所のトレードオフを解決することを目指すものです。

また、特に強化学習を用いるメリットは、ルールや達成したい目的のみから、supervisionやドメイン知識無しで自律的に学習を進めることができる点で、ヒューリスティクスに準ずる(もしくは置き換わる)ような求解パターンを、ルールのみからスクラッチ学習しようという試みとなっています。
この試みに関して、一年ほど前にUCIのグループから論文「Solving the Rubik's Cube Without Human Knowledge」が出ており、今回はその概要を簡単な実装例と実験結果を通してご紹介させていただきます。
強化学習アルゴリズムについて
強化学習の基礎学習アルゴリズムとして今回は、「モデルフリー」で「方策学習」ベースのA2Cアルゴリズム2を用いました。一方、上記参照論文では「モデルベース」で「方策学習」ベースの(動的計画法の一種である)Policy Iteration3に基づいたアルゴリズムを用いています。加えて、それら基礎アルゴリズムで学習された方策に「モデルベース」のMonte Calro Tree Search(MCTS)アルゴリズムをポストプロセスとして組み合わせ、予測の更なる精度向上を図っています。
強化学習アルゴリズムは、各アルゴリズムの特徴に基づき、対象課題の特性に沿って選択、組み合わされます。その意味でもアルゴリズムの大きな分類を把握できていると全体の見通しが良くなるかと思いますので、以下に今回関連している代表的な分類である、価値/方策学習、モデルフリー/ベースに関して簡単に纏め、今回の手法選択の背景をご説明することにします。(他にも方策オン/オフ、前方/後方観測などの重要な分類もありますが今回は割愛することにします。)
価値学習か、方策学習か
| 手法 | 典型例 | 長所 | 短所 |
|---|---|---|---|
| 価値学習 | DQN, DDQN | - 学習が安定しやすい | - "方策"は状態価値から二次的に表現 |
| 方策学習 | REINFORCE | - 最終目的である"方策"を直接的に表現 | - 局所解に陥りやすい |
- 「価値学習」アルゴリズムは、各状態(+行動)の価値を、今後獲得される(であろう)報酬に基づき学習することを目指します。学習に際して、状態価値が局所的に無矛盾に表現できているか(ベルマン誤差)を保証するように学習を進めるため、学習が安定しやすくなっています。一方、当初の目的である”各状態においてどのような行動を取るべきか”を与える方策は、状態価値関数に基づき、より良い行動を取るように間接的に表現されます。
- 一方、「方策学習」アルゴリズムは、方策に基づいて行動を進めた際に獲得される(であろう)報酬を最大化するように、より良い方策を(関数変換等なく)直接的に学習します。本来の目的である”方策”を直接的に学習する一方で、学習データへの依存(バリアンス)が大きくなる傾向があり、ハイパーパラメタへの依存性が大きくなったり、局所解に陥り易くなる傾向があります。
近年、互いの欠点を補うようなより良い学習アルゴリズムが検討される中で、一定条件下での「価値学習」と「方策学習」の等価性が示されている様に4、実はどちらの学習法でも本質的には同様の表現が可能であることが分かってきています。一方、課題応用に際しては、求められる表現や加えたい制約条件、実装的な制約などに基づき、対象課題を扱いやすいアルゴリズムが選択されているように伺えます。特に、
1. ターン制のボードゲームなど、複雑で戦略的な行動選択が求められる課題
2. ロボットアームのアクチュエータの連続制御など、高次元で行動自由度の高い課題
に対しては、方策の表現を直接的に保持、評価、工夫するメリットが大きくなり、方策学習に基づいたアルゴリズムが選ばれる傾向が強くなっています。本ルービックキューブの課題においては、上記1.(下記モデルベース手法との組合せ観点を含む)を鑑みて、方策ネットワークを直接的に学習するActor-Criticアルゴリズム^5を採用しました。
モデルフリーか、モデルベースか
| 手法 | 典型例 | 長所 | 短所 |
|---|---|---|---|
| モデルフリー | A2C, DQN | - 環境に依存せず、限られたデータのみから学習が可能 | - 詳細な学習には時間が掛かる |
| モデルベース | MCTS, 動的計画法 | - 環境に沿った詳細な学習が可能 | - 学習データの網羅的な探索が求められる |
- 「モデルフリー」アルゴリズムは、エージェントが環境の詳細(遷移確率)を知ることなく、行動による環境への働きかけとその返り値である報酬や次の状態のみから学習を進めるアルゴリズムです。環境を常にブラックボックスの学習対象として扱い、環境の(確率的)反応も内包した方策や状態価値を学習していきます。特定の環境に依存しない汎用性の高い学習が限られたデータのみから可能である一方、データ効率が悪く詳細な学習にはより多くのデータを必要とし、学習に時間が掛かる傾向にあります。
- 一方、「モデルベース」アルゴリズムは、対象の環境が明示的にモデル化されている/モデル化することを前提とし、モデル化された環境を活用し先を予測したり、状態系列を戻したりしながら、方策や状態価値の学習を進めます。環境に寄り添ったデータ効率の良い詳細な学習が可能になる一方、環境をモデル化するために網羅的な状態探索が必要になる傾向にあります。
今回の様な小さい課題(可能な行動選択も考慮すべき行動系列も10オーダー)に対しては、網羅探索の計算コストが小さいため「モデルベース」の手法が用いられ易く、そのため、上記参照論文では実際、「モデルベース」の手法が基礎学習手法として用いられています。一方、囲碁や将棋のような大きな課題に対しては、「モデルフリー」のアルゴリズムが基礎になることが多くなっています。今回の取り組みでは、今後のより複雑な課題への発展も考慮し、「モデルフリー」のアルゴリズム(A2C)を基礎とすることにしました。
実際の課題応用においては、これらも組み合わせれて用いられることが多く、実際AlphaGo5では、「モデルベース」のMCTSアルゴリズムが(学習された方策ネットワークに基づき)さらに高精度の将来予測を行うためのポストプロセスとして活用され、戦略決定アルゴリズムの重要な一部分を担っています。同様に、上記参照論文でも、MCTSアルゴリズムをポストプロセスとして用いることで行動選択の精度を大幅に向上させています。今回の取り組みでも、MCTSをポストプロセスとして活用し、基礎方策のみに基づくナイーブな戦略に対し、確かに精度向上が見られるかを確認することにしました。
実装例
実装例の全体は Githubを参照いただくとして、実装の基礎となる内容のみ簡単に記載します。
シミュレーター環境について
まず、強化学習の学習の基礎となるシミュレーターについてです。様々な方がルービックキューブのシミュレーターの実装を公開していらっしゃいますが、今回は、状態空間の試行錯誤や自身の理解のためにも、[OpenAI Gymの枠組み]
(https://qiita.com/ohtaman/items/edcb3b0a2ff9d48a7def)で簡単に自前実装することにしました。今回は簡単のため、3x3x3、2x2x2のキューブ (order = 3, 2) のみ想定していますが、より大きなキューブへの拡張も容易かと思います。
今回実装したシミュレーターの各要素の概要は以下の通りです。
| 概要 | 表現 | |
|---|---|---|
| 状態 (state) | 各面の各タイルセグメントにどの色付きタイルが配置されているかの状態 | タイルの色をone-hotで表現した、order x order x 6(face) x 6(color)次元のベクトル |
| 行動 (action) | グローバル回転を除外した(固定ブロック/軸を保持した)、可能な面/スライスの回転操作(上図参照) | - 2x2x2: (F, R, U), - 3x3x3: (F, R, U, B, L, D) + 逆回転(反時計回り), etc. |
| 報酬 (reward) | 状態に応じた報酬 | - 終端であれば +1 - それ以外は -1
|
| 終端 (done) | 解けた状態かどうか | - 解けたら True - それ以外は False
|
回転操作の実装としては、操作に関係する周辺タイルを一度 (order+2, order+2) の行列にマップし、numpyの操作を用いて90°回転を行っています。また、操作の対称性を考慮し、キューブ全体を回転させるようなグローバルな回転は実装しておらず、指定面(スライス)を回転させる操作のみを考えています。
対称性やキューブ構造の制約に伴って、本来は考慮すべき状態ベクトルもより小さい次元での表現が可能となりますが、今回は簡単のため、冗長ですが最も単純な上記の様なone-hot表現を用いました。
以下の試行では、2x2x2のルービックキューブに対して、(F, F', R, R', U, U')(Xの逆回転操作をX'で表現)という6つの90°回転操作を行う環境("quarter-turn metric"と呼ばれる6)を採用し実験を行いました。
構築ネットワークと学習について
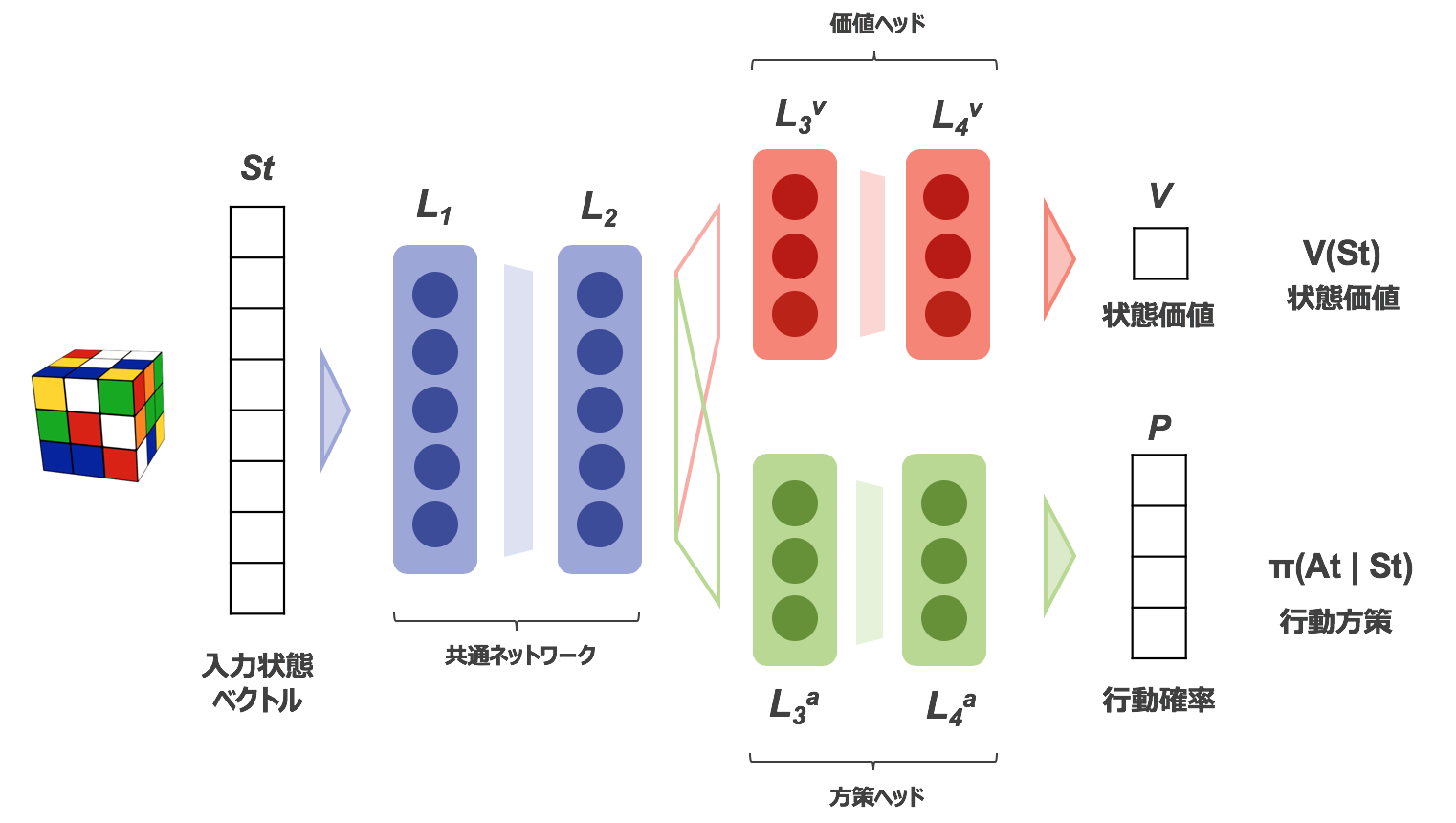
A2Cアルゴリズムでは、方策ネットワークと価値ネットワークを更新・学習しますが、今回はシェアされた共通ネットワークをもち、入力であるキューブ状態から、方策(次の各行動の確率)と価値(入力状態の価値)を与える二つのヘッドを持つ一つのネットワークを学習することにしました。
オリジナルのAlphaGoでは、教師あり学習による事前学習結果の転移活用も考慮に入れ、別ネットワークとしていましたが、(事前学習を用いない)AlphaGo Zeroの論文7では、別々のネットワークを用いる場合と比較して、計算効率や複数の目的に跨る(汎用性の高い)共通の表現の獲得によってより良い結果が得られたことが報告されています。切り替えは容易ではありますが、今回はその単純さから2ヘッドのネットワークを活用しました。
学習ターゲットであるデータの生成(探索)に関しては、解かれた状態から(可能な回転操作の中から)ランダムに選択された回転操作を指定回数だけ行い、その状態から強化学習の試行錯誤の探索手続きを実行しました。ランダム操作の回数は、参照論文に従い、より解に近い(回数が少ない)サンプルが多くなるように(1/操作回数の重みで)生成しました。(この重みづけによって、確かにより精度の高い方策が学習できることも確かめられました。)
A2Cの学習アルゴリズムの概要を記載すると以下のようになります。現在の方策ネットワークに基づき(方策オンで)行動選択を行い、環境にアクセスしながら自身で探索を行い(self-play)、獲得した報酬の情報を用いて、方策や価値ネットワークの重みを更新します。今回の課題のような手続き系列の学習に際しては、(TD$(0)$ではなくTD$(\lambda)$の様に)系列情報を明示的に保持して学習に活用することが、学習効率を向上させるために一層重要になります。今回は、episode内の獲得報酬情報を保持し、ネットワークの更新の際に重み付き報酬和($G_T$)を明示的に再構成する、いわゆる前方観測によって更新を行いました。
import tensorflow as tf
import RubiksCubeEnv, ActorCriticAgent, Memory
# --- PRE-PROCESS ---
# session start
sess = tf.Session()
# make instances
env = RubiksCubeEnv()
agent = ActorCriticAgent()
memory = Memory()
# --- TRAIN MAIN ---
# episode loop
for i_episode in range(n_episodes):
# reset environment
env.reset()
# initial cube scramble
_, state = env.apply_scramble()
# step loop
for i_step in range(n_steps):
# obtain action prediction from policy network
action = agent.get_action(sess, state)
# obtain reward for the action
next_state, reward, done, _ = env.step(action)
# memory push
memory.push(state, action, reward, next_state, done)
state = next_state
if done:
break
# --- POST-PROCESS (EPISODE) ---
# retrieve episode data
memory_data = memory.get_memory_data()
# update model with the episodic data
_args = zip(*memory_data)
losses = agent.update_model(sess, *_args)
# reset memory for next episode
memory.reset()
class ActorCriticAgent(object):
def __init__(self):
...
def update_model(self, sess, state, action, reward, next_state, done):
...
# calculate value target & TD error
# TD(0)
if 0:
next_st_val = self.predict_value(sess, next_state)
target_val = reward + self.gamma * next_st_val
# TD(\lambda)
if 1:
# re-order rewards to construct Gt
target_val = []
for i_step in range(len(reward)):
reward_seq = [self.gamma**i * i_reward[0]
for i, i_reward in enumerate(reward[i_step:])]
g_t = np.sum(reward_seq)
target_val.append([g_t])
st_val = self.predict_value(sess, state)
td_error = target_val - st_val
# define feed_dict
feed_dict = {input: state, val_obs: target_val, td_err: td_error,
act_obs: action_idx}
# update value network
_, losses = sess.run([self.value_optim, self.losses], feed_dict)
# update policy network
_, losses = sess.run([self.policy_optim, self.losses], feed_dict)
return losses
方策学習後のポストプロセスについて
次に、A2Cアルゴリズムによって学習された方策ネットワークを用いた予測に関してです。
前項で述べた様に、方策ネットワークを直接用いる予測よりも、追加の探索時間は必要となりますが、MCTSをポストプロセスとして追加することで、精度が大きく向上することが報告されています。今回用いたMCTSは、PUCTアルゴリズムと呼ばれる(rolloutを用いない)学習ネットワークを全面的に信頼、活用したアルゴリズムで、AlphaGo Zeroでも用いられているものです。(ただしAlphaGo Zeroではポストプロセスだけではなく、self-playによる学習ターゲットの生成にも同様のMCTSを用いています。)
本MCTSの概要を記載すると以下のようになります。
**1. Select:**既存の探索木の中から、各ノードの価値(V)と選択確率(P)に基づいた一定の選択条件によって子ノードを順次選択しながら報酬情報を収集
**2. Expand:**終端ノードに達したら更なる子ノードを展開し、各ノードの選択確率(P)を”推定方策”に基づいて付与
**3. Evaluate and Backup:**通ってきた行動経路/列によって得られた報酬情報や終端ノードの”推定状態価値”を用いて、該当経路の価値を評価し、関連各ノードの価値(V)を更新
**4. Repeat:**1へ戻る
これを繰り返し木探索を終了条件が満たされるまで繰り返します。”推定方策”や"推定状態価値"に既に学習された方策、価値ネットワークを用いることで、探索木を全探索することなく目ぼしいノードに絞りながら状態の探索と評価を効率的に進めることが可能になります。
ノード選択条件の詳細などは上記論文などを参照いただくとして、基本的な方針は、上記P、Vに基づき各ノードに対して算出される 平均状態価値 ($Q(s, a) \propto $ 累積報酬総和/ノード訪問数) と ノード探索価値 ($U(s, a) \propto $ 選択確率/ノード訪問数) から、$a_t = \text{argmax}_a (Q(s_t,a_t)+U(s_t,a_t))$ によって、探索と活用のバランスを取りながら選択していきます。
# Class of Monte Carlo Tree Search
class MCTS(object):
# constructor
def __init__(self, agent):
self.env = RubiksCubeEnv()
self.agent = agent
# run search to find best path
def run_search(self, sess, root_state):
# --- PRE-PROCESS ---
# create root node of this search
root_node = Node(None, None, None)
# record best path
best_reward = float('-inf')
best_solved = False
best_actions = []
# --- SEARCH MAIN ---
start_time = time.time()
# loop of search runs
while True:
# initialization
node = root_node
state = root_state
self.env.set_state(root_state)
weighted_reward = 0.0
done = [False]
actions = []
# drill down existing tree nodes with a selecting rule until its terminal
n_depth = 0
while node.child_nodes:
# select a node among child nodes
node = self._select_next_node(node.child_nodes)
# evaluate the node
next_state, reward, done, _ = self.env.step(node.action)
weighted_reward += self.gamma**n_depth * reward[0]
n_depth += 1
state = next_state
actions.append(node.action)
# expand the terminal node when its not done
if not done[0]:
# calc probs of each action at the terminal node
action_probs = self.agent.predict_policy(sess, [state])
# expand child nodes from the terminal
node.child_nodes = [Node(node, act, act_prob) for act, act_prob
in zip(self.action_list, action_probs[0])]
# evaluate the terminal state value when its not done
if not done[0]:
# utilize state value of the terminal node, (no rollout)
_v_s = self.agent.predict_value(sess, [state])
weighted_reward += self.gamma**n_depth * _v_s[0][0]
# non-complete penalty
weighted_reward += self.unsolved_penalty
# update node params, following back the node path
while node:
node.n += 1
node.v += weighted_reward
node = node.parent_node
# update best path
if best_reward < weighted_reward:
best_reward = weighted_reward
best_solved = done[0]
best_actions = actions
# termination criteria
duration = time.time() - start_time
if duration >= self.time_limit:
break
return best_reward, best_solved, best_actions
# Class of Node Container
class Node(object):
def __init__(self, parent, action, prob):
# its parent node
self.parent_node = parent
# action taken to arrive
self.action = action
# probability to arrive at this node from parent
self.p = prob
# state value of this node
self.v = 0.0
# number of visits of this node
self.n = 0
# child nodes associated to this node
self.child_nodes = []
試行結果
ここまでご紹介したアルゴリズムに基づいて、2x2x2のルービックキューブの学習を進めた結果、以下の様な結果が得られました。今回は各アルゴリズム紹介と基本傾向の把握を主としているため、学習は簡易的に行っています。
A2Cアルゴリズムによる学習/推定結果
まず、A2Cアルゴリズムによる方策/価値ネットワークの学習を行いました。簡単のため、学習はローカルラップトップで1時間程度で終了するepisode数で行いました。左下図に平均損失と平均報酬の推移を示しています。ランダムな方策からスタートし、確かにepisodeの進行によって期待報酬が向上しているのが確認できます。また、今回は、episode毎でのネットワーク更新(バッチサイズ15(ステップ)程度)を行っていますが、価値ネットワーク(ベースライン)の導入によって、ある程度バリアンスが抑えられた学習が行えていることも分かります。
学習された方策ネットワークを用いて、別のテストデータに対して、どの程度ルービックキューブが確かに解かれ得るかをプロットしたものが右図になります。今回は学習された方策ネットワークのみを用い、各状態に対して方策ネットワークの出力確率に基づき、次の行動を選択して状態を推移させています。横軸は解状態からランダムに回転操作した回数で、縦軸はそのうち実際に解けた割合を表しています。学習プロットから分かる通り、1, 2回の操作に対してはよく解を導けているものの、6, 7回辺りからは5割程度しか解けていないのが分かります。(ランダム方策では、凡そ $(1/6)^n = (0.17)^n$ になることにも留意ください。)
実際の遷移サンプルを示したものが以下になります。右向きの遷移がランダムに回転操作を行なった際の記録で、左向きの遷移が方策ネットワークによって選択された回転操作です。また各状態には、価値ネットワークが与える状態価値の値も記載しています。
解けている例:

以下、簡単のため全てコマンドラインにて表現していきます。
Scrambles: 2, 536/536
G | --[R']--> --[F']--> | S
G | <--[R]-- (1.31) <--[F]-- (0.29) | S
Scrambles: 4, 496/518
G | --[R]--> --[U]--> --[U]--> --[F]--> | S
G | <--[R']-- (1.21) <--[U']-- (0.57) <--[U']-- (-0.43) <--[F']-- (-10.02) | S
Scrambles: 6, 342/486
G | --[F]--> --[F]--> --[F']--> --[U']--> --[U']--> --[F']--> | S
G | <--[F']-- (1.13) <--[U]-- (2.01) <--[U]-- (-1.22) <--[F]-- (-12.02) | S
Scrambles: 8, 248/498
G | --[R']--> --[U]--> --[U]--> --[F']--> --[U]--> --[R']--> --[F']--> --[F]--> | S
G | <--[R]-- (1.31) <--[U']-- (0.20) <--[U']-- (-0.06) <--[F]-- (-10.18) <--[U]-- (-12.67) <--[U]-- (-11.84) <--[U]-- (-17.50) <--[R]-- (-16.78) | S
多回転操作で解けているものは、(X+X')のような冗長な操作が含まれ、実質少ない操作で解けるものが多くまれていました。また、選択操作についてもUx3(=U')など冗長な表現も含まれがちです。
解けていない例:
Scrambles: 4, 22/518
G | --[R]--> --[F']--> --[U']--> --[R']--> | S
* <--[R]-- (-8.44) <--[R]-- (-10.68) <--[U']-- (-3.49) <--[U]-- (-10.68) <--[R']-- (-8.44) <--[R]-- (-10.68) <--[F]-- (-10.60) <--[U]-- (-12.93) <--[F']-- (-10.13) <--[F]-- (-12.93) <--[F]-- (-11.18) <--[R]-- (-10.36) <--[U]-- (-7.00) <--[U]-- (-13.74) <--[U]-- (-7.81) | S
Scrambles: 6, 144/486
G | --[F']--> --[R]--> --[R]--> --[U]--> --[F]--> --[U']--> | S
* <--[R']-- (-12.14) <--[U]-- (-12.96) <--[U']-- (-12.14) <--[R]-- (-15.32) <--[R']-- (-12.14) <--[R]-- (-15.32) <--[F]-- (-15.66) <--[U]-- (-13.88) <--[U]-- (-12.74) <--[U]-- (-11.92) <--[F]-- (-8.69) <--[F']-- (-11.92) <--[F']-- (-10.07) <--[U]-- (-11.29) <--[R]-- (-15.29) | S
Scrambles: 8, 250/498
G | --[U]--> --[R]--> --[R]--> --[R]--> --[R']--> --[U]--> --[R]--> --[U']--> | S
* <--[R']-- (-9.04) <--[R]-- (-8.03) <--[R']-- (-9.04) <--[R]-- (-8.03) <--[R']-- (-9.04) <--[R]-- (-8.03) <--[R']-- (-9.04) <--[R]-- (-8.03) <--[R']-- (-9.04) <--[U']-- (-10.61) <--[R']-- (-6.85) <--[R']-- (-10.02) <--[U']-- (-9.74) <--[R]-- (-12.29) <--[U]-- (-11.78) | S
今回の報酬の定義を考慮すれば、状態価値(や方策)が正しく推定されていれば、各状態価値は解から離れるにしたがっておおよそ-1で減少していくことが期待されます。一方、上記例からは、2、3回の操作を越えると、それら期待される値から大きく乖離した状態価値が各状態に付与されており、それらの状態の価値がネットワークによって(まだ)正しく推定できてないことが分かります。特に、解けていない例においては、行動操作によって状態価値が上昇しておらず、各状態に対してその価値や適切な方策が正しく推定できていなことが、顕著に伺えます。一層学習を進め、これらの価値を正しく推定できる様になっていくことを通して、上記解答率曲線が改善していくことが予想されます。
A2C + MCTSアルゴリズムによる推定結果
次に、テストデータに対して、A2Cで学習された方策/価値ネットワークに基づいてMCTSアルゴリズムによるポストプロセス処理を行い、得られた結果が以下のプロットになります。

解答率の曲線が明らかに大きく向上しているのが見て取れるかと思います。
上記と同様にこの時の遷移サンプルを示したものが以下になります。
解けている例:
Scrambles: 6, 504/526
G | --[F']--> --[R']--> --[U]--> --[R']--> --[R']--> --[U]--> | S
G | <--[F]-- (0.89) <--[R]-- (0.06) <--[U']-- (-0.29) <--[R']-- (-11.72) <--[R']-- (-14.34) <--[U']-- (-19.36) | S
Scrambles: 7, 471/515
G | --[F']--> --[F']--> --[R']--> --[F']--> --[R]--> --[R]--> --[U']--> | S
G | <--[F']-- (1.13) <--[F']-- (0.14) <--[R]-- (-1.69) <--[F]-- (-7.61) <--[R']-- (-10.43) <--[R']-- (-9.58) <--[U]-- (-12.97) | S
Scrambles: 8, 440/527
G | --[F]--> --[F]--> --[R']--> --[F']--> --[U]--> --[F]--> --[R]--> --[U']--> | S
G | <--[F]-- (0.89) <--[U']-- (0.78) <--[R']-- (-0.87) <--[U]-- (-8.39) <--[F]-- (-12.67) <--[U]-- (-15.65) | S
Scrambles: 9, 358/472
G | --[F]--> --[R']--> --[R]--> --[U']--> --[U']--> --[U']--> --[R']--> --[R']--> --[F]--> | S
G | <--[F']-- (1.13) <--[U']-- (-0.04) <--[R']-- (-1.04) <--[R']-- (-7.84) <--[F']-- (-15.58) | S
状態価値の評価の不十分さに伴って、一時的に状態価値が減少する様な操作も含みながら、長い操作列や冗長な操作列に対しても、より効率的な操作手順(U'x3をUで対応)を推定できていることが見て取れます。また、8回転操作の例では、逆順とは異なる、より短い操作列(6操作)を見つけられていることも分かります。
解けていない例:
Scrambles: 7, 44/515
G | --[U']--> --[R']--> --[F]--> --[U]--> --[F']--> --[R]--> --[U']--> | S
* <--[U']-- (-7.49) <--[F]-- (-12.53) <--[U]-- (-16.16) | S
Scrambles: 8, 87/527
G | --[F']--> --[U]--> --[U]--> --[F']--> --[R]--> --[R]--> --[F]--> --[F]--> | S
* <--[F']-- (-7.45) <--[U']-- (-5.17) <--[F']-- (-6.55) <--[U]-- (-6.71) <--[F']-- (-10.45) <--[U]-- (-14.78) <--[R]-- (-10.14) <--[F']-- (-19.06) | S
Scrambles: 9, 114/472
G | --[U']--> --[R]--> --[U']--> --[F']--> --[F']--> --[U]--> --[U']--> --[U']--> --[U']--> | S
* <--[F']-- (-4.30) <--[U']-- (-3.19) <--[F]-- (-5.79) <--[F]-- (-6.82) <--[U']-- (-12.63) <--[R']-- (-12.41) <--[U']-- (-19.56) | S
Scrambles: 10, 179/495
G | --[U]--> --[F]--> --[R]--> --[R]--> --[F]--> --[R']--> --[U]--> --[U]--> --[R]--> --[F]--> | S
* <--[R']-- (-2.27) <--[F]-- (-8.30) <--[U']-- (-5.89) <--[F]-- (-8.38) <--[U]-- (-15.96) <--[U]-- (-16.01) | S
一方、上記の様に解を発見できていない系列も未だある程度見受けられました。しかしながら、最終状態の状態価値の値を見る限り、ネットワークの改善やハイパラ調整、探索時間の延長などで改善が見込める様に伺えます。
前記のナイーブな推定の際と同様に、ネットワークによる状態価値の推定は未だ不十分である状況ですが、今回の様に、木探索による適切な活用と探索を行うことによって、微妙な状態価値の差を考慮(活用)したり、時には価値が悪化する方向に振る(探索)ことによって、期待される解の遷移を効果的に発見し得ることが分かります。(結果は活用と探索の重みパラメタ、探索時間などハイパーパラメターに大きく依存することにご留意ください。今回の探索時間に関しては、ネットワークによる解推定0.1 [s]に対して、MCTSでは10倍の1.0 [s]程度の探索・推定を許す様な環境に設定しています。)
この様に、学習された方策が大まかでも、それらをMCTSに活用することである程度の質の解が得られ、性能を大きく改善し得ることが伺えました。AlphaGo Zeroではこの性質をより積極的に活用し、方策・価値ネットワーク学習のターゲット生成に際してもMCTSを活用し、協力的に学習を進めるアイディアが活用されています(まとめ章の図参照)。
これら以上の結果は、上記参照論文でも同様なことが報告されており、学習方策基づいてMCTSを用いた解推定を行うことで初めて、推定精度や推定速度の両観点から既存のベストヒューリスティクスを凌駕する性能を発揮することが報告されています。ちなみに、ルービックキューブに関しては、網羅探索によって、God's Numberと呼ばれる、任意シャッフル状態を解くために必要となる回転操作数の上限値が示されています5。論文でもその観点から、得られた解がヒューリスティクス解に対し、いかにより良い解を与えているかの比較も行われており、大変興味深い結果が示されています。また、学習された解の中によく知られた定石パターンが多く含まれてることも示されており、ご興味のある方は一読いただけると面白いかと思います。
教師あり学習による学習/推定結果
最後に、A2Cによる方策学習の比較対象として、方策ネットワークについて教師あり学習を行なった結果を示しておこうと思います。教師としてはランダム回転させた際の各回転を各状態に対しる解として保持し、学習を行いました。強化学習と同様、解に近いサンプルの適当な重みづけは必要でしたが、A2Cと同程度のサンプル数のデータに対して得られた結果は、以下の様な曲線でした。

予想通り、教師あり学習の強化学習(A2C)に対するデータ効率の良さが見て取れます。AlphaGo Zeroの報告でも、教師あり学習の初期学習効率の良さが示されています。実課題適用を考える際に、まず初期アプローチとして(AlphaGoの例のように)教師あり学習を用いて方策を明示的に学習するのは筋が良さそうです。一方、最終的には強化学習が教師に依存しない、無駄の少ないより良い戦略を獲得する様になることが報告されています。今回の課題でも、上記サンプルで既に一部見られたように、必ずしも回転させる手続きを逆に辿る行動系列が最適とは限らず、より詳細を探ってゆくことで同様の傾向が得られることが十分予想されます。また、今回は教師ありとの比較でしたが、参照論文で用いられたpolicy iterationとのデータ効率の比較も興味深いかと思います。
最後に、今回簡易的に得られた結果をより改善していくためのアプローチとしては、
■ ロングランや非同期化などによって学習データを増やし、そもそもの方策・価値ネットワークを賢くしていく
■ 今回は学習の振舞いを確認しながらざっくり行なったA2C、MCTSのハイパーパラメタの調整
■ 学習データの工夫(例:X+X'の様な冗長な組合せを除外。実は今回の環境では1/6の確率で逆操作となるため、10回操作すると80%以上は必ず冗長な手続きを含んでしまう。)
■ AlphaGo Zeroの様に学習過程(ターゲット)にMCTSを用いる
などが挙げられ、今後適宜検討していこうと思っています。
まとめ
今回はルービックキューブのパズルを、機械学習、特に強化学習で解くアプローチをご紹介しました。簡易的に試行したのみではありますが、身近なパズルに対しても、機械学習によるアプローチが検討され得ることをご理解いただければ幸いです。この例のように、機械学習によって、既存のドメイン知識をデータに基づいて再構築し直したり、互いに補うことで、より有効なビジネス活用を模索するケースは今後も増えてくるのではないかと考えています。
また、各アルゴリズムの紹介でも度々登場するしているように、今回の参照論文もAlphaGo7 8のアプローチに大きく影響を受けており、各構成要素は基本的には同様なものとなっています。
参考:AlpahGo Zeroの学習アルゴリズム概要図8


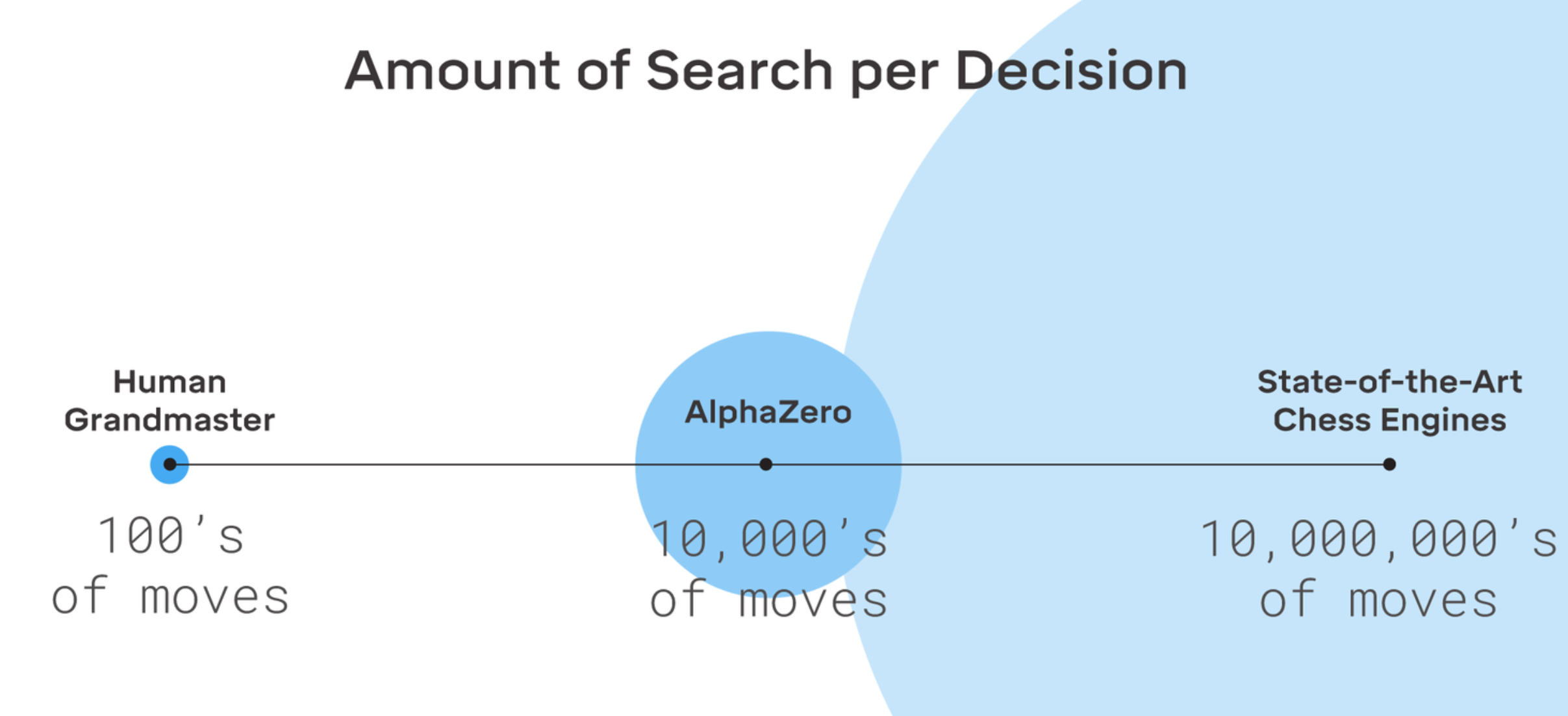
今回のご紹介したアルゴリズムを、非同期化するなど適宜拡張・効率化していただくことで、より複雑な対戦ボードゲームやハイパーパラメターチューニングの様な、多様な行動選択を重ねて最適解を目指す課題に対しても、効率的に課題を解くアプローチとして検討いただけるのではないかと思います。実際、先日の最新のAlphaZeroのリリース9においても、広く様々なボードゲームに対して、強化学習による方策/状態価値の学習によって探索が桁違いに効率化されたことが強調されています。
その意味でも今回のルービックキューブの課題は、良い基礎を与える課題と感じ、取り組みをご紹介させていただきました。
これら強化学習アルゴリズムや探索アルゴリズムは、より効率的な手法の模索が現在も精力的に続けられており10、また開発コミュニティの活発な貢献によって、実装の敷居も大きく下がってきています11。今後もそれらの掛け算でより良い求解アルゴリズムが提案、実装されていくと思われます。引き続きこれらの発展を注意深く見守って行くとともに、その実務応用可能性を模索していきたいと考えています。
-
Combining policy gradient and Q-learning, Bridging the Gap Between Value and Policy Based Reinforcement Learning, Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor ↩
-
90°(X), 270°(X')回転のみでなく180°回転(X+X)も1操作とする"half-turn metric"という基準も存在 ↩
-
Mastering the game of Go with Deep Neural Networks & Tree Search ↩ ↩2
-
AlphaZero: Shedding new light on the grand games of chess, shogi and Go ↩