画像同士で類似している部分を探索するため手法の一つであるテンプレートマッチングの理論と実装についてまとめています。
テンプレートマッチングとは
入力画像の中からテンプレート画像と最も類似する場所を探索することをテンプレートマッチングと呼びます
| 入力画像 | テンプレート画像 |
|---|---|
 |
 |
画像の例の場合、テンプレート画像と同じ部分が最も類似すると判断されるよう探索されるのがよいテンプレートマッチングとなります。
テンプレートマッチングは、入力画像の一部とテンプレート画像との 類似度 を求めます。
全座標で類似度を求めることで最も類似する部分は判断しています。
基本的にはテンプレート画像と入力画像を重ねたときのそれぞれの画素同士を比較していくので、スケールや回転にはロバストではありません。
最近の手法としてはスケールや回転にも対応している輪郭サーチを用いたマッチングが用いられることが多いです。
テンプレートマッチングにおける類似度の計算方法にはいくつか代表的なものがあり、本記事ではSSD,SAD,NCC,ZNCCの4種類について紹介します。
これらの手法は画像に限らず 何らかの類似度を求める場合 において参考となる式なので覚えておくと役に立つかもしれません。
定義
計算方法については以降は関数Rとして説明します。
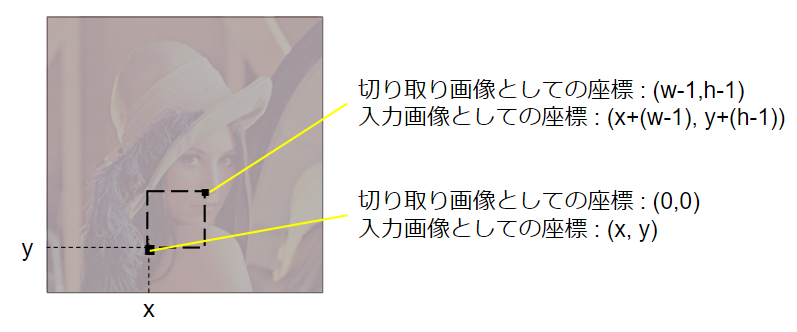
$R(x,y)$ : 座標(x,y)を基準としてテンプレート画像を重ねた場合のマッチングのスコア。各走査位置に対してスコアを求め、最もよいもの/閾値を超えるものをマッチングしたと判断します。
また、本記事では数式を用いて解説を行うために、変数名を以下のように定義しています。
入力画像とテンプレート画像を重ね合わせるときに基準となる座標(走査位置) : $(x,y)$
テンプレート画像の幅 : $w$
テンプレート画像の高さ : $h$
入力画像の幅 : $w_I$
入力画像の高さ : $h_I$
入力画像の画素値 : $I(a,b)\quad※aはx座標, bはy座標$
テンプレート画像の画素値 : $T(a,b)\quad※aはx座標, bはy座標$
画素値
画像を構成する最小要素を 画素またはピクセル と呼び、この1画素に対して光の強さや色を表した数値を 画素値 と呼びます。
カラー画像は赤(R)、緑(G)、青(B)の3原色の状態で様々な色を表現しています。
1画素のRGB要素をそれぞれ0~255で表しており、例えば赤、白、黒は以下のような画素値となります。
- 赤: (R 255, G 0, B 0)
- 白: (R 255, G 255, B 255)
- 黒: (0, 0, 0)
また、1画素を白黒の濃淡で表現することもでき、これをカラー画像に対してグレースケール画像といいます。
グレースケール化した画像では、1画素は0~255で構成されます。
本記事ではグレースケール化した画像を想定した計算式となっています。
計算式1. SSD(Sum of Squared Difference)
SSDは重なった2つの画像の各セルについて、画素値の二乗誤差の総和となります。
テンプレート画像と切り取り画像が全く同じ場合、SSDの値は0となります。
したがって、値が小さいほど似ている位置となります。
$$R_{SSD}(x,y) = \displaystyle\sum^{h-1}_{j=0} \sum^{w-1}_{i=0} {(I(x+i,y+j) - T(i,j))}^2$$
全体的に暗い場合や明るい場合でも検出しやすい式となりますが、
一部だけ画素値に異常な差がある場合は検出されないことがあります。
計算式2. SAD(Sum of Absolute Difference)
SADは入力画像とテンプレート画像の重なった各セルについて、画素値の誤差の絶対値の総和となります。
先ほどのSSDで二乗だったものを絶対値に置き換えた式になります。
こちらもテンプレート画像と切り取り画像が全く同じ場合、SSDの値は0となり小さいほど似ている位置となります。
$$R_{SAD}(x,y) = \displaystyle\sum^{h-1}_{j=0} \sum^{w-1}_{i=0} |(I(x+i,y+j) - T(i,j))|$$
二乗誤差を用いない分SSDよりは一部の異常な画素値の差も許容することができます。
また、計算の早さはSSDよりも優れています。
計算式3. 正規化相互相関【NCC:Normalized Cross-Correlation】
NCCは重なった部分に対して相関係数を求めるような式となります。
$$R_{NCC}(x, y) = \frac{\displaystyle\sum^{h-1}_{j=0} \sum^{w-1}_{i=0}I(x+i,y+j)×T(i, j)}{\displaystyle\sqrt{\sum^{h-1}_{j=0} \sum^{w-1}_{i=0}{{I(x+i,y+j)}^2}}×{\sqrt{\sum^{h-1}_{j=0} \sum^{w-1}_{i=0}{{T(i,j)}^2}}}}$$
ここで、一般的な2データ間の相関係数の公式は次のとおりです。
$$R(x, y) = \frac{\displaystyle\frac{1}{n}\sum^{n}_{i=1}(x_i-\bar{x})×(y_i-\bar{y})}
{\displaystyle\sqrt{\frac{1}{n}\sum^{n}_{i=1} {{(x_i-\bar{x})}^2}}×{\sqrt{\frac{1}{n}\sum^{n}_{i=1} {{(y_i-\bar{y})}^2}}}}$$
$\bar{x}$は$x$の平均
$\bar{y}$は$y$の平均
式を比較してみると、偏差を画素値に置き換えた式になっていることがわかります。
一般的な相関係数と同様で、$R_{NCC}$の値は0.0~1.0の範囲に収まり、数値が高いほど類似していると判定されます。
このNCCをより相関係数の式に近づけたものが次に説明するZNCCとなります。
計算式4. 正規化相互相関【ZNCC:Zero-mean Normalized Cross-Correlation】
画素値から画像全体の画素値の平均を引いた状態で計算を行います。
$\mu_{I(x,y)}$は入力画像の走査位置に対する各セルの画素値の平均
$\mu_T$はテンプレート画像の各セルの画素値の平均
$$\mu_{I(x,y)} = \frac{1}{w_Ih_I}\displaystyle\sum^{h_I-1}_{j=0}\sum^{w_I-1}_{i=0}I(x+i, y+j)$$
$$\mu_T = \frac{1}{wh}\displaystyle\sum^{h-1}_{j=0}\sum^{w-1}_{i=0}T(i, j)$$
$$R_{ZNCC}(x, y) = \frac{\displaystyle\sum^{h-1}_{j=0} \sum^{w-1}_{i=0}(I(x+i,y+j)-\mu_{I(x,y)})×(T(i, j)-\mu_T)}{\displaystyle\sqrt{\sum^{h-1}_{j=0} \sum^{w-1}_{i=0}{{(I(x+i,y+j)-\mu_{I(x,y)})}^2}}×{\sqrt{\sum^{h-1}_{j=0} \sum^{w-1}_{i=0}{{(T(i,j)-\mu_T)}^2}}}}$$
$R_{ZNCC}$の値は-1.0~1.0の範囲に収まり、数値が高いほど類似していると判定されます。
簡単なデータで手動計算
入力画像を4×4の画像として、画素値を
\begin{pmatrix}
1 & 2 & 3 & 4 \\
5 & 6 & 7 & 8 \\
8 & 7 & 6 & 5 \\
4 & 3 & 2 & 1
\end{pmatrix}
テンプレート画像を2×2の画像として、画素値を
\begin{pmatrix}
5 & 6 \\
6 & 5
\end{pmatrix}
として実際に計算を行ってみます。
SSD
各走査位置についてSSDを計算していきます。
\begin{aligned}
R_{SSD}(0,0) &= \displaystyle\sum^{h-1}_{j=0} \sum^{w-1}_{i=0} {(I(x+i,y+j) - T(i,j))}^2\\
&= \displaystyle\sum^{2-1}_{j=0} \sum^{2-1}_{i=0} {(I(0+i,0+j) - T(i,j))}^2\\
&= \displaystyle\sum^{1}_{j=0} \sum^{1}_{i=0} {(I(i,j) - T(i,j))}^2\\
&= (I(0,0)-T(0,0))^2+(I(0,1)-T(0,1))^2+(I(1,0)-T(1,0))^2+(I(1,1)-T(1,1))^2\\
&= (1-5)^2+(2-6)^2+(5-6)^2+(6-5)^2\\
&= 16 + 16 + 1 + 1\\
&= 34\\
\end{aligned}
$R_{SSD}(0,1) = (2-5)^2+(3-6)^2+(6-6)^2+(7-5)^2 = 22$
$R_{SSD}(0,2) = (3-5)^2+(4-6)^2+(7-6)^2+(8-5)^2 = 18$
$R_{SSD}(1,0) = (5-5)^2+(6-6)^2+(8-6)^2+(7-5)^2 = 8$
$R_{SSD}(1,1) = (6-5)^2+(7-6)^2+(7-6)^2+(6-5)^2 = 4$
$R_{SSD}(1,2) = (7-5)^2+(8-6)^2+(6-6)^2+(5-5)^2 = 8$
$R_{SSD}(2,0) = (8-5)^2+(7-6)^2+(4-6)^2+(3-5)^2 = 18$
$R_{SSD}(2,1) = (7-5)^2+(6-6)^2+(3-6)^2+(2-5)^2 = 22$
$R_{SSD}(2,2) = (6-5)^2+(5-6)^2+(2-6)^2+(1-5)^2 = 34$
小さいほどよいため、全ての走査位置で最もSSDがよいのは走査位置$(x,y)=(1,1)$となります。
SAD
\begin{aligned}
R_{SAD}(0,0) &= \displaystyle\sum^{h-1}_{j=0} \sum^{w-1}_{i=0} |(I(x+i,y+j) - T(i,j))|\\
&= \displaystyle\sum^{2-1}_{j=0} \sum^{2-1}_{i=0} |(I(0+i,0+j) - T(i,j))|\\
&= \displaystyle\sum^{1}_{j=0} \sum^{1}_{i=0} |(I(i,j) - T(i,j))|\\
&= |I(0,0)-T(0,0)|+|I(0,1)-T(0,1)|+|I(1,0)-T(1,0)|+|I(1,1)-T(1,1)|\\
&= |1-5|+|2-6|+|5-6|+|6-5|\\
&= 4 + 4 + 1 + 1\\
&= 10
\end{aligned}
$R_{SAD}(0,1) = |2-5|+|3-6|+|6-6|+|7-5| = 8$
$R_{SAD}(0,2) = |3-5|+|4-6|+|7-6|+|8-5| = 8$
$R_{SAD}(1,0) = |5-5|+|6-6|+|8-6|+|7-5| = 4$
$R_{SAD}(1,1) = |6-5|+|7-6|+|7-6|+|6-5| = 4$
$R_{SAD}(1,2) = |7-5|+|8-6|+|6-6|+|5-5| = 4$
$R_{SAD}(2,0) = |8-5|+|7-6|+|4-6|+|3-5| = 8$
$R_{SAD}(2,1) = |7-5|+|6-6|+|3-6|+|2-5| = 8$
$R_{SAD}(2,2) = |6-5|+|5-6|+|2-6|+|1-5| = 10$
小さいほどよいため、全ての走査位置で最もSSDがよいのは走査位置$(x,y)=(1,0),(1,1),(1,2)$となります。
NCC
\begin{aligned}
R_{NCC}(0, 0) &= \frac{\displaystyle\sum^{2-1}_{j=0} \sum^{2-1}_{i=0}I(0+i,0+j)×T(i, j)}{\displaystyle\sqrt{\sum^{2-1}_{j=0} \sum^{2-1}_{i=0}{{I(0+i,0+j)}^2}}×{\sqrt{\sum^{2-1}_{j=0} \sum^{2-1}_{i=0}{{T(i,j)}^2}}}}\\
&= \frac{\displaystyle\sum^{1}_{j=0} \sum^{1}_{i=0}I(i,j)×T(i, j)}{\displaystyle\sqrt{\sum^{1}_{j=0} \sum^{1}_{i=0}{{I(i,j)}^2}}×{\sqrt{\sum^{1}_{j=0} \sum^{1}_{i=0}{{T(i,j)}^2}}}}\\
&= \frac{I(0,0)×T(0,0)+I(0,1)×T(0,1)+I(1,0)×T(1,0)+I(1,1)×T(1,1)}
{\sqrt{{I(0,0)}^2+{I(0,1)}^2+{I(1,0)}^2+{I(1,1)}^2}
×{\sqrt{{T(0,0)}^2+{T(0,1)}^2+{T(1,0)}^2+{T(1,1)}^2}}}\\
&= \frac{1×5+2×6+5×6+6×5}
{\sqrt{1+4+25+36}×\sqrt{25+36+36+25}}\\
&= \frac{77}
{\sqrt{66}×\sqrt{122}}\\
&= 0.858\\
\end{aligned}
\begin{aligned}
R_{NCC}(0,1) &= \frac{2×5+3×6+6×6+7×5}{\sqrt{4+9+36+49}×\sqrt{25+36+36+25}} = 0.905\\
R_{NCC}(0,2) &= \frac{3×5+4×6+7×6+8×5}{\sqrt{9+16+49+64}×\sqrt{25+36+36+25}} = 0.942\\
R_{NCC}(1,0) &= \frac{5×5+6×6+8×6+7×5}{\sqrt{25+36+64+49}×\sqrt{25+36+36+25}} = 0.988\\
R_{NCC}(1,1) &= \frac{6×5+7×6+7×6+6×5}{\sqrt{36+49+49+36}×\sqrt{25+36+36+25}} = 0.999\\
R_{NCC}(1,2) &= \frac{7×5+8×6+6×6+5×5}{\sqrt{49+64+36+25}×\sqrt{25+36+36+25}} = 0.988\\
R_{NCC}(2,0) &= \frac{8×5+7×6+4×6+3×5}{\sqrt{64+49+16+9}×\sqrt{25+36+36+25}} = 0.932\\
R_{NCC}(2,1) &= \frac{7×5+6×6+3×6+2×5}{\sqrt{49+36+9+4}×\sqrt{25+36+36+25}} = 0.905\\
R_{NCC}(2,2) &= \frac{6×5+5×6+2×6+1×5}{\sqrt{36+25+4+1}×\sqrt{25+36+36+25}} = 0.851\\
\end{aligned}
1に近いほどよいため、全ての走査位置で最も$R_{NCC}$がよいのは走査位置$(x,y)=(1,1)$となります。
ZNCC
\begin{aligned}
R_{ZNCC}(0, 0) &= \frac
{\displaystyle\sum^{2-1}_{j=0} \sum^{2-1}_{i=0}(I(0+i,0+j)-\mu_{I(0,0)})×(T(i, j)-\mu_T)}
{\displaystyle\sqrt
{\sum^{2-1}_{j=0} \sum^{2-1}_{i=0}{{(I(0+i,0+j)-\mu_{I(0,0)})}^2}}
×{\sqrt
{\sum^{2-1}_{j=0} \sum^{2-1}_{i=0}{{(T(i,j)-\mu_T)}^2}}}}\\
&= \frac
{\displaystyle\sum^{1}_{j=0} \sum^{1}_{i=0}(I(i,j)-\mu_{I(0,0)})×(T(i, j)-\mu_T)}
{\displaystyle\sqrt
{\sum^{1}_{j=0} \sum^{1}_{i=0}{{(I(i,j)-\mu_{I(0,0)})}^2}}
×{\sqrt
{\sum^{1}_{j=0} \sum^{1}_{i=0}{{(T(i,j)-\mu_T)}^2}}}}\\
&= \frac{
(I(0,0)-\mu_{I(0,0)})×(T(0,0)-\mu_T)
+ (I(0,1)-\mu_{I(0,0)})×(T(0,1)-\mu_T)
+ (I(1,0)-\mu_{I(0,0)})×(T(1,0)-\mu_T)
+ (I(0,0)-\mu_{I(1,1)})×(T(1,1)-\mu_T)
}
{
\sqrt{
{(I(0,0)-\mu_{I(0,0)})}^2
+ {(I(0,1)-\mu_{I(0,0)})}^2
+ {(I(1,0)-\mu_{I(0,0)})}^2
+ {(I(1,1)-\mu_{I(0,0)})}^2
}
× \sqrt{
{(T(0,0)-\mu_T)}^2
+{(T(0,1)-\mu_T)}^2
+{(T(1,0)-\mu_T)}^2
+{(T(1,1)-\mu_T)}^2
}
}\\
&= \frac{(1-14/4)×(5-22/4)+(2-14/4)×(6-22/4)+(5-14/4)×(6-22/4)+(6-14/4)×(5-22/4)}
{\sqrt{(1-14/4)^2+(2-14/4)^2+(5-14/4)^2+(6-14/4)^2}×\sqrt{(5-22/4)^2+(6-22/4)^2+(6-22/4)+(5-22/4)^2}}\\
&= \frac{0}
{\sqrt{17}×\sqrt{1}}\\
&= 0\\
\end{aligned}
\begin{aligned}
R_{ZNCC}(0,1) &= \frac{0}{\sqrt{17}×\sqrt{1}} = 0\\
R_{ZNCC}(0,2) &= \frac{1}{\sqrt{5}×\sqrt{1}} = 0\\
R_{ZNCC}(1,0) &= \frac{1}{\sqrt{5}×\sqrt{1}} = 0.447\\
R_{ZNCC}(1,1) &= \frac{1}{\sqrt{1}×\sqrt{1}} = 1\\
R_{ZNCC}(1,2) &= \frac{1}{\sqrt{5}×\sqrt{1}} = 0.447\\
R_{ZNCC}(2,0) &= \frac{0}{\sqrt{17}×\sqrt{1}} = 0\\
R_{ZNCC}(2,1) &= \frac{0}{\sqrt{17}×\sqrt{1}} = 0\\
R_{ZNCC}(2,2) &= \frac{0}{\sqrt{17}×\sqrt{1}} = 0\\
\end{aligned}
1に近いほどよいため、全ての走査位置で最も$R_{ZNCC}$がよいのは走査位置$(x,y)=(1,1)$となります。
OpenCVを用いたPythonでの実装
画像処理ライブラリOpenCVには計算を行ってくれるcv2.matchTemplateメソッドが実装されているので、Pythonでは簡単に処理を作ることができます。
cv2.matchTemplateメソッドはパラメータで入力画像とテンプレート画像と類似度の計算方法を指定します。
類似度の計算方法は以下が使用できます。
- cv2.TM_SQDIFF : 計算方法1のSSD
- cv2.TM_SQDIFF_NORMED : 計算方法1のSSDを正規化(計算方法3の分母で割る)
- cv2.TM_CCORR : 計算方法3のNCCの分母を消した式
- cv2.TM_CCORR_NORMED : 計算方法3のNCC
- cv2.TM_CCOEFF : 計算方法4のZNCCの分母を消した式
- cv2.TM_CCOEFF_NORMED : 計算方法4のZNCC
今回はこちらの画像を使用して、テンプレートマッチングを行いました。
| 入力画像 | テンプレート画像 |
|---|---|
 |
 |
# module
import cv2
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 画像の読み込み
img = cv2.imread('./Lenna.png')
template = cv2.imread('./Lenna_template.png')
# グレースケール化
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
template_gray = cv2.cvtColor(template, cv2.COLOR_BGR2GRAY)
# テンプレートマッチングの実行
result = cv2.matchTemplate(img_gray, template_gray, cv2.TM_CCOEFF_NORMED)
resultにはテンプレートマッチングで計算した全走査位置の類似度が渡されます。
img_gray.shape
# (256, 256)
template_gray.shape
# (31, 31)
result.shape
# (226, 226)
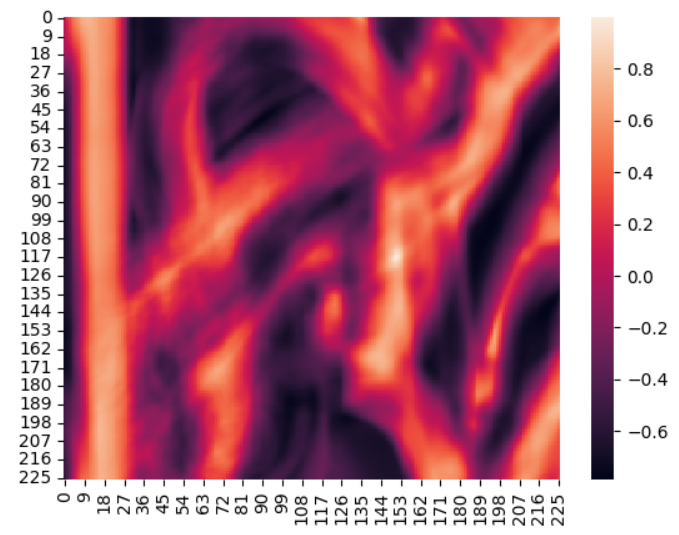
sns.heatmap(result)
ヒートマップで真っ白になっている(153, 117)付近が高いことを確認できました。
実際にはテンプレート画像のサイズが31×31画素のため(153, 117),(153, 147), (183, 117), (163, 147)の4点で囲まれた部分が最も類似していることになります。
入力画像にマッチングした位置を描画してみると、テンプレート画像と同じ位置が選ばれていることがわかります。
# マッチング位置を描画
cv2.rectangle(img_gray, (153, 117), (183, 147), 255, 2)
plt.imshow(img_gray, cmap='gray')