なにを解くのか
おそらく一部のみだろうが、韓国軍やドイツがコロナウイルスの検体を混ぜて検査(プール検査)しているそうだ。
では、プール検査を前提とした時に、どれだけ効率よく検査できるのか。今回はそれを調べてみる。なお、あくまでも数学的興味からの計算であり、究極の理想的な状況を仮定しているため、この結果をそのまま実用には供することは難しい。
前提として次の仮定を置き、必要なPCR検査回数の平均の最小値を求める。
- 何らかの事前情報があり、各人が確率$p$で感染していることが分かっている。
- 検査結果に応じて、次にどの検体を検査するかを動的に決めて良い。
- 混ぜた検体をテストして、中に1人でも陽性者がいれば陽性、全くいなければ陰性が出る。中間値などは得られない。
- 同じ人から何度でも検体を採取可能で、採取にかかるコストは考えない。
- 偽陰性、偽陽性は発生しない。
動的計画法による解法
最適な検査プロセスを採用した状況で、$n$人全員の陽性・陰性を確定させるまでの平均検査回数を$f_1(n)$とし、これを求めたい。補助関数$f_2(n),r(n,x)$を作り、これらの値を次のように再帰的に求めてみた。
$f_1(n)$:$n$人の感染状況に関して($p$以外の)情報がない場合平均検査回数
$f_2(n)$:$n$人の中に陽性者がいることが分かっている場合の平均検査回数
$r(n,x)$:$n$人のうち少なくとも$1$人が陽性であると判明している場合に、その中から選んだ$x$人に陽性者がいない条件付確率を表す関数
$ f_1(n)=\min_{1 \leq x \leq n} 1+ \{ 1-(1-p)^x \} f_2(x)+f_1(n-x) $
$f_2(n)=\min_{1 \le x \le n-1}1+\{1-r(n,x)\}\{f_2(x)+f_1(n-x)\}+r(n,x)f_2(n-x)$
$r(n,x)=\frac{(1-p)^x \{1-(1-p)^{n-x}\}}{1-(1-p)^n}$
$f_1(n)$の解説:「$x$人分を混ぜての検査が$1$回。これが陽性になる確率は$1-(1-p)^x$。その$x$人には陽性の場合にのみ検査しこれが$f_2(x)$回。残り$n-x$人にはいずれの場合も検査が必要で$f_1(n-x)$回検査」→$x=1, 2, \cdots , n$でこの最小値を$f_1(n)$とする。
$f_2(n)$の解説:「$x$人分を混ぜての検査が$1$回。これが陽性になる確率は$1-r(n,x)$。陽性の場合はその$x$人の検査$f_2(x)$回と残り$n-x$人の検査$f_1(n-x)$回、陰性の場合は残り$n-x$人のみに陽性がいるので$f_2(n-x)$回の検査」→$x=1, 2, 3, \cdots , n-1$でこの最小値を$f_2(n)$とする。
$r(n,x)$の解説:($x$人が全員陰性かつ$n$人の中に陽性者がいる確率)/($n$人の中に陽性者がいる確率)=($x$人が全員陰性の確率)×(残りの$n-x$人に陽性者がいる確率)/($n$人の中に陽性者がいる確率)
また、明らかに$f_1(0)=0, f_2(1)=0$である。($f_2(0)$は$0$人中に陽性がいるはずがないので定義できない。)これらの式を元に、$f_1(1)$→$f_2(2)$→$f_1(2)$→$f_2(3)$→$f_1(3)$→$\cdots $→$f_1(n)$の順番で計算を積み上げれば良い。動的計画法である。Mathematicaでは、値をキャッシュさせれば計算順序を考えなくても普通に値が求まる。(たらいまわし関数なども楽に計算可)
さらに、$f_1(n), f_2(n)$の計算において、どの$x$により最小値を出したかを表す関数を$s_1(n), s_2(n)$として、これも求めておく。これらは、各段階においていくつの検体を混ぜて検査すべきかの戦略を示すことになる。
#Mathematicaで書く
Mathematicaプログラムはこんな感じ。
ClearAll[f1,f2,s1,s2]
$RecursionLimit = Infinity;
r[n_,x_,p_] :=(1-p)^x(1-(1-p)^(n-x))/(1-(1-p)^n);
f1[n_,p_]:=({f1[n, p],s1[n,p]}= MinimalBy[Table[{1+(1-(1-p)^x)f2[x,p]+f1[n-x,p],x},{x,1,n}],First][[1]])[[1]];
f2[n_,p_]:=({f2[n,p],s2[n,p]}= MinimalBy[Table[{1+(1-r[n, x,p])(f2[x, p]+f1[n-x,p])+r[n,x,p]f2[n-x,p],x},{x,1,n-1}],First][[1]])[[1]];
f1[0,p_]=0;
f2[1,p_]=0;
$p=0.001, 0.002, \cdots , 0.01$について、$n=1000$まで$f_1(n)$の値をプロットするとこうなる。
ListPlot[Table[f1[n,p],{p,.01,.001,-.001},{n,1,100}],Joined->True,PlotLegends->Table["p="<>ToString[p],{p,.01,.001,-.001}],AxesLabel->{Style["n",Medium],Style["f_1(n)",Medium]}]

$n=100$でも、$p$が十分に小さければかなり少ない検査回数で済むことが分かる。
#検査回数の分布
最適戦略を取った場合の検査回数の分布も見てみる。モンテカルロで実行してみると面白い形になる。
m = 200000;(*モンテカルロ回数*)
p = 0.001;
n = 1000;
f1[n,p];(*これをあらかじめ計算しておかないとs1,s2が計算されない。*)
data = RandomVariate[BernoulliDistribution[p], {m, n}];
(*0,1の数字を確率1-p,pでm×n個発生させる。*)
k1[d_] := Module[{d1 = d[[1 ;; s1[Length[d], p]]], d2 = d[[s1[Length[d], p] + 1 ;;]]},
1 + If[Plus @@ d1 > 0, k2[d1] + k1[d2], k1[d2]]];
(*与えられた0,1の列をs1[Length[d]]以前とそれより後に分割。前者の試験で陽性が出るか否かで場合分け。*)
k2[d_] := Module[{d1 = d[[1 ;; s2[Length[d], p]]], d2 = d[[s2[Length[d], p] + 1 ;;]]}, 1 + If[Plus @@ d1 > 0, k2[d1] + k1[d2], k2[d2]]];
(*与えられた0,1の列をs2[Length[d]]以前とそれより後に分割。前者の試験で陽性が出るか否かで場合分け。*)
k1[{}] = 0;
k2[{1}] = 0;
dist = ParallelMap[k1, data];
Histogram[dist, {1}, "PDF"]
$n=1000, p=0.001$ではこんな分布になる。
!コメント 2020-04-25 012637.png
$n=1000, p=0.01$ではこう。
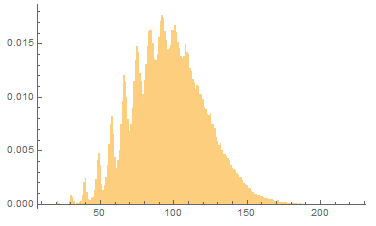
#どう検査すべきか
具体的な$n$と$p$が与えられた時の検査手順については、$s_1(n), s_2(n)$を見れば良い。各段階で、次に何人の検体を混ぜて検査すべきが分かる。$p=0.01$でグラフにすると、かなり複雑な形になる。(青が$f_1(n)$、オレンジが$f_2(n)$)このグラフは実数化せずに計算したが、機械精度実数では誤差が出て少し違う形になる。
p = 1/100;
f1[500, p];
DiscretePlot[{s1[n, p], s2[n, p]}, {n, 0, 500}]
もっと具体的なテスト手順を求めてみる。
p = 0.2
f1[5, p];
d = Range[5];
k1[d_] := Module[{d1 = d[[1 ;; s1[Length[d], p]]],
d2 = d[[s1[Length[d], p] + 1 ;;]]},
Style[test @@ d1, Red][pos[k2[d1], k1[d2]], neg[k1[d2]]]];
k2[d_] := Module[{d1 = d[[1 ;; s2[Length[d], p]]],
d2 = d[[s2[Length[d], p] + 1 ;;]]},
Style[test @@ d1, Red][pos[k2[d1], k1[d2]], neg[k2[d2]]]];
k1[{}] = Nothing;
k2[{x_}] := Nothing;
k1[d] //. {pos[Nothing, x_] | pos[x_, Nothing] -> pos[x],
pos[Nothing, Nothing] | pos[Nothing] -> pos,
neg[Nothing, x_] | neg[x_, Nothing] -> neg[x],
neg[Nothing, Nothing] | neg[Nothing] | neg[{}] -> neg} // TreeForm
これは$n=5, p=0.2$の場合。一番上の$test[1,2]$は、検体$1$と$2$を混ぜてテストすることを意味している。この結果が陽性(pos)ならばさらに検体$1$の単独テストと検体$3,4,5$を混ぜたテストを実施。それらの結果に基づいて、さらに下の階層へと進む。最初のテストが陰性(neg)ならば検体$3,4,5$を混ぜてテスト。もしこの結果が陰性ならば、全員の陰性が確定する。
#その他の解法
動的計画法を考える前は、各段階において最も大きな平均情報量が得られるように、つまり陽性・陰性がちょうど五分五分に分かれるように混ぜる人数を再帰的に選んでいく方法を試みていた。この場合、
$s_1(n)=\min(n,-\frac{\log(2)}{\log(1-p)})$
$s_2(n)=\min(n-1,\frac{\log\{1+n(1-p)\}-\log 2} {\log 1-p})$
となる。(実際には整数にする必要があるので、切り上げまたは切り下げをして陽性率50%に近い方を採用する必要がある。)いずれにせよ、動的計画法の方法よりも少し回数が多くなる。部分最適化が全体最適化ではないことや、他の細々したことが原因だと思われる。ただ、最適解とはそれほど大きな差はないようにも見える。
また、ポール・J・ナーインの「ちょっと手強い確率パズル」に同じ問題が載っている。ただし、これは$n$人を$k$グループに分割して各グループ毎に混ぜたものを検査し、陽性が出たグループは全員を再検査するというもの。$k$の最適解は$\frac{1}{\sqrt p}$であり、平均検査回数は$n \{1+\sqrt p-(1-p)^\frac{1}{\sqrt p}\}$。動的計画法より手数がかかる。
動的計画法よりも良い方法はあるだろうか?私はこれが最適解だと思うが、さらに上回る方法を見つけた人は知らせていただきたい。また今回は平均を最小にしたが、現実的には「PCRの試験は$10$回まで行える。$10$回を超える検査が必要となる確率を最小にしたい」「採取器具の使用数や全員分が判明するまでの時間も含めて最小化したい」のようなものの方が需要が高いかもしれない。おそらく別の戦略が必要になる。

