標高差を考慮した本当の距離を算出してみた

はじめに

本記事ではある地点からある地点までの距離を求める際に、標高を加味した本当の距離を算出します。通常のMap上に表示される距離は標高差を考慮していない距離だと思われます。（もし違ったらすみません。）そこで、本当の距離を出すべくスタート地点からゴール地点までの標高差を考慮しながら距離を算出してみます。

今回のコードはヘルシンキ大学が公開しているGISに関する教材を元にしています。
筆者はそちらの教材を勉強した後のアウトプットでこの記事を書いています。
GISについて勉強してみたい方はぜひそちらを使ってみてください。そちらの教材についての質問があればQiitaのコメントで議論させていただけると、筆者も勉強になり大変嬉しいです。

※本記事はGoogle Colab上で使用することを想定しています。ローカル環境でのコード実行時には事前に必要なライブラリのインストールが必要になります。

扱うデータについて

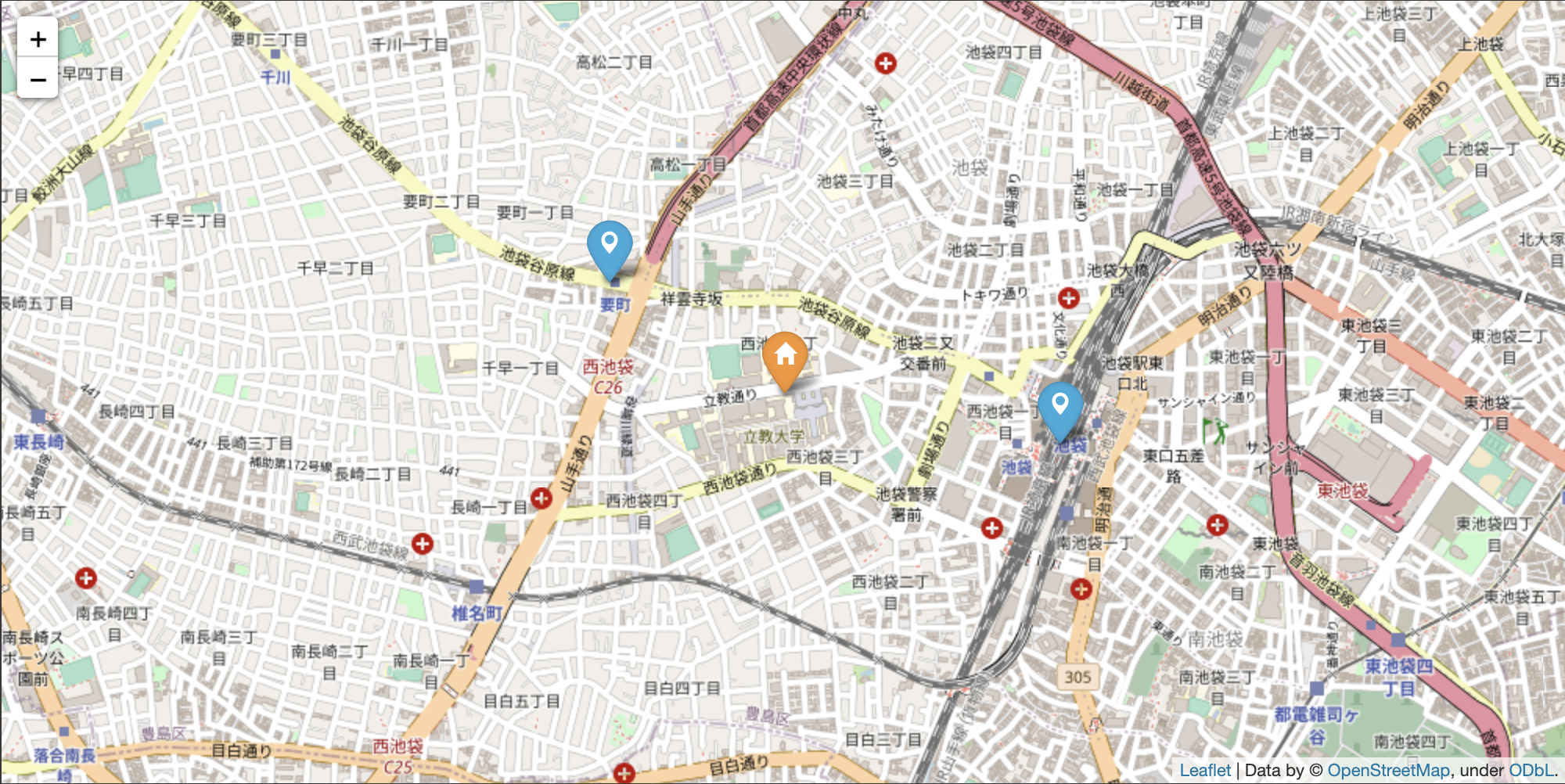
本記事ではスタート地点を立教大学とし、ゴール地点を池袋駅、要町駅とします。立教大学のホームページではどちらの駅も最寄り駅とされていますが、実際どちらの駅の方が近いのかを標高を加味した距離を算出して確認します。

各地点の緯度経度
・立教大学：35.7308109, 139.7032871
・池袋駅：35.7297031, 139.7108572
・要町駅：35.7332654, 139.6985205

スタート地点とゴール地点を地図に表示する

まずは必要なライブラリをインポートします。

!pip install geopandas
!pip install osmnx
!pip install contextily

スタート地点、ゴール地点はそれぞれ適当なcsvファイルに記入します。
今回はスタート地点1つに対して、2つのゴール地点について調査しますが、スタート地点を複数にすることも可能です。
下のプログラムはcsvファイルに記載した全スタート地点×全ゴール地点の全パターンの距離を算出します。
今回の例だと、以下のようなcsvファイルを作成します。

・origins.csv(立教大学）

x	y
139.7032871	35.7308109

・destinations.csv（池袋駅、要町駅）

x	y
139.7108572	35.7297031
139.6985205	35.7332654

csvファイルを読み込んでmapに表示します。

import folium
import pandas as pd

fp_org = '/content/drive/MyDrive/~/origins.csv' # スタート地点ファイル格納場所を記載してください。
fp_dst = '/content/drive/MyDrive/~/destinations.csv' # ゴール地点ファイル格納場所を記載してください。

df_org = pd.read_csv(fp_org)
df_dst = pd.read_csv(fp_dst)

# 枠作成
f = folium.Figure(width=1000, height=500)

# 中心地検索
med_org = df_org.median()
med_dst = df_dst.median()

# 初期表示の中心の座標を指定して地図を作成する。
center_org_lat=med_org['y']
center_org_lon=med_org['x']

map = folium.Map([center_org_lat,center_org_lon], zoom_start=15).add_to(f)
    
# スタート地点マーカー作成(オレンジ)
for i in range(len(df_org)):
    folium.Marker(location=[df_org['y'][i],df_org['x'][i]], icon=folium.Icon(color="orange", icon="home"), popup=str(df_org['y'][i])+","+str(df_org['x'][i])).add_to(map)
# ゴール地点マーカー作成(青)
for i in range(len(df_dst)):
    folium.Marker(location=[df_dst['y'][i],df_dst['x'][i]], icon=folium.Icon(color="blue", icon="map-marker"), popup=str(df_dst['y'][i])+","+str(df_dst['x'][i])).add_to(map)

map

スタート地点がオレンジ、ゴール地点が青で表示されています。

指定地点の標高を取得する

GEEのデータを使用するため、GEEの認証を行います。
GEE認証を実行すると認証に必要なURLが表示されるので、URLへアクセスしてGoogleアカウントを指定し、表示された認証コードをGoogle Colabのボックスへコピペしてください。

import ee
import pandas as pd
import csv

try:
 ee.Initialize()
except Exception as e:
 ee.Authenticate()
 ee.Initialize()

GEEからデータをロードし、リストで返却する関数を定義します。

def load_data(snippet, geometry, band):
   # パラメータの条件にしたがってデータを抽出
   dataset = ee.ImageCollection(snippet).filter(
   ee.Filter.geometry(geometry)).select(band)
   # リスト型へ変換
   data_list = dataset.toList(dataset.size().getInfo())
   # データリストを出力
   return data_list

今回はALOSのDSMというバンドを利用します。
実は衛星データから標高を算出する方法は以前、別記事で投稿しています。よろしければご参照ください。
登山好きプログラミング素人が衛星データで登りたい山を探してみた！〜②衛星データで周囲で一番高い山を探してみる編〜

## パラメーターの指定
# 衛星を指定
snippet = 'JAXA/ALOS/AW3D30/V3_2'
# バンド名を指定
band = 'DSM'

画像から関心領域の最大値を取得する関数を定義します。
reducerを用いて画像の最大値を取得し、返しています。

def get_max(aoi):
 data_list = load_data(snippet=snippet, geometry=aoi, band=band)
 image = ee.Image(data_list.get(0))
 max = image.reduceRegion(reducer=ee.Reducer.max(), geometry=aoi, scale=30)
 return max.values().getInfo()[0]

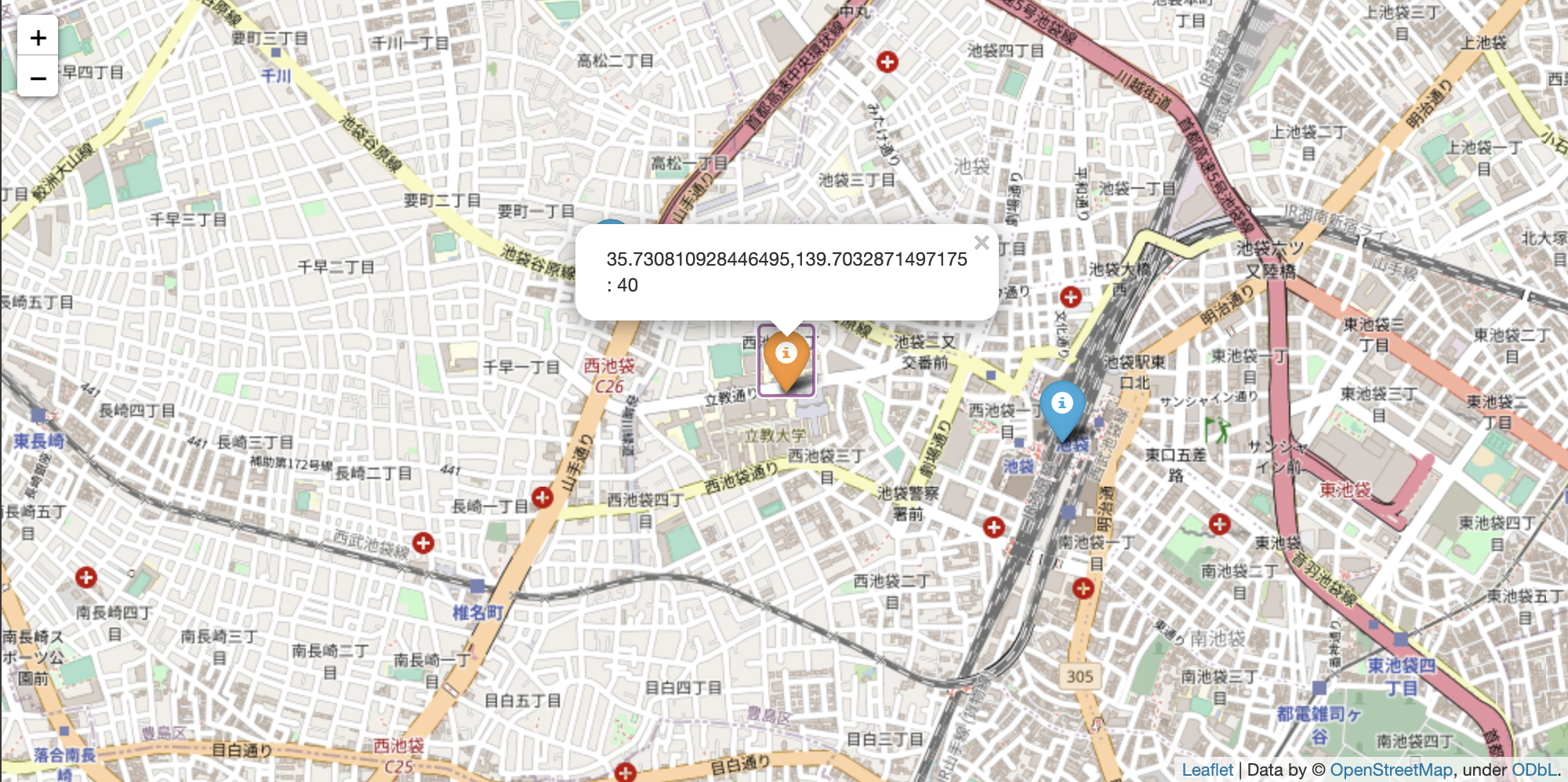
スタート地点、ゴール地点の標高を取得し、map上のマーカーに標高を表示してみます。

# スタート地点標高取得&マーカー修正
for i in range(len(df_org)):
    lat = df_org['y'][i]
    lon = df_org['x'][i]

    poi = ee.Geometry.Point([lon, lat])
    org_max = get_max(poi)
    folium.Marker(location=[df_org['y'][i],df_org['x'][i]], icon=folium.Icon(color="orange"), popup=str(df_org['y'][i]) + "," + str(df_org['x'][i]) + " : " + str(org_max)).add_to(map)

# ゴール地点標高取得&マーカー修正
for i in range(len(df_dst)):
    lat = df_dst['y'][i]
    lon = df_dst['x'][i]

    poi = ee.Geometry.Point([lon, lat])
    dst_max = get_max(poi)
    folium.Marker(location=[df_dst['y'][i],df_dst['x'][i]], icon=folium.Icon(color="blue"), popup=str(df_dst['y'][i]) + "," + str(df_dst['x'][i]) + " : " + str(dst_max)).add_to(map)

map

緯度, 経度 : 標高(m)の情報が追加されています。

すこし寄り道しますが、各緯度経度からその地点の名称を確認することができます。リバースジオコーディング等と言うそうです。
確認してみて分かりましたが、要町駅ではなく要町駅付近の駐輪場が指定されているそうです。ただ、要町駅は地下鉄ですし、距離的に大差ないので今回は誤差を無視します。

from geopy.geocoders import Nominatim
geolocator = Nominatim(user_agent="org")


# スタート地点の緯度経度リバースジオコーディング
print('Starts-------------')
for i in range(len(df_org)):
    location = geolocator.reverse([df_org['y'][i], df_org['x'][i]])
    if location is None:
        print(str(i) + ' : ' + 'Anknown')
    print(str(i) + ' : ' + str(location.address))

# ゴール地点の緯度経度リバースジオコーディング
print('Goals-------------')
for i in range(len(df_dst)):
    location = geolocator.reverse([df_dst['y'][i], df_dst['x'][i]])
    if location is None:
        print(str(i) + ' : ' + 'Anknown')
    print(str(i) + ' : ' + str(location.address))

Starts-------------
0 : 立教大学, 西池袋通り, 西池袋三丁目, 豊島区, 東京都, 171-0021, 日本
Goals-------------
0 : 池袋, Main Footway, 南池袋一丁目, 南池袋, 豊島区, 東京都, 171-8569, 日本
1 : 要町駅路上自転車駐車場, 池袋谷原線, 要町二丁目, 豊島区, 東京都, 171-0043, 日本

スタート~ゴール間の途中点を取得し、実距離を算出する

スタート地点とゴール地点の情報は上記にて分かりました。スタート地点とゴール地点の標高差から三平方の定理を用いて斜辺の値を出せば標高差を加味した距離になる、というのはあまりにもおざなりなので、できるだけ近い地点同士で距離を出し、スタート地点からゴール地点までの全中継点ごとの距離を合計します。
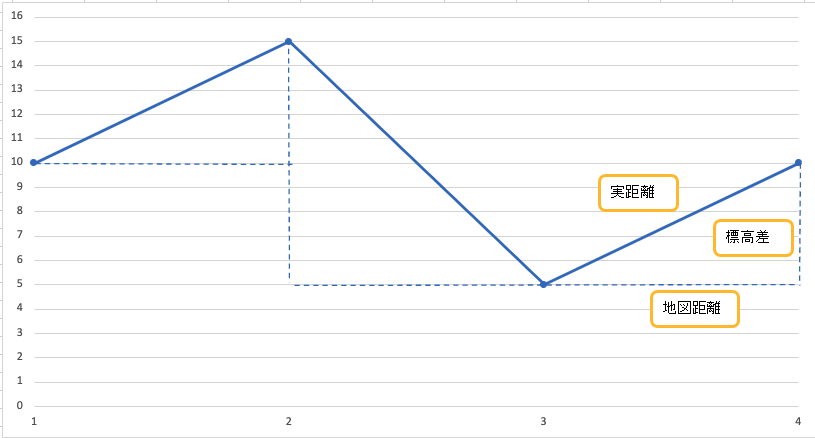
イメージ的には以下の絵になります。スタート地点からゴール地点までを横から見たときのイメージです。
各点から次の点までの地図上の距離と標高差から三平方の定理を用いて実距離を算出します。この時、スタート地点からゴール地点までの途中点を細かくすればするほど誤差が小さくなります。
実距離^2 = 地図距離^2 + 標高差^2にて実距離（標高差を加味した距離）を算出していきます。

ここからはスタート地点からゴール地点までの途中点を取得していきます。
OpenStreetMapを用いた道路ネットワークはNetworkXを用いて操作できます。
詳細は以下のサイトが参考になります。

まずは、スタート地点からゴール地点までの全ての地点を包括するエリアを特定します。
そのために全地点をpandasのDataFrameに格納します。

# 全ポイントの結合
df_all = pd.concat([df_org, df_dst])
print(df_all)

x y
139.703287 35.730811
139.710857 35.729703
139.698521 35.733265

次に全地点を含むPolygonを作成します。

# Polygonの作成
from shapely.geometry import Polygon

coordpairs = list(zip(df_all.x, df_all.y))
poly = Polygon(coordpairs)
print(poly)
poly

作成したPolygonから緯度経度の最大値である境界値を取得します。

# bboxの作成(minx, miny, maxx, maxy)
bbox = poly.bounds
print(bbox)

(139.6985205, 35.72970309811198, 139.71085718240985, 35.7332654)

全地点を含む境界に対しバッファを与え、扱う地図範囲を完全に全地点を含む境界にします。
この時に与えるバッファに決まりはありませんが、あまりに小さいと自身が設定した緯度経度のポイントにノード情報が存在しない可能性があり、その場合一番近くノードを使用することになりますが、本来一番近くのはずのノードが地図上に含まれなくなってしまう可能性があります。

# Buffer付与
graph_extent = rec.buffer(0.05)
print(graph_extent)
graph_extent

最初の境界より少し広がっていることを確認します。

# バッファ付与後の境界
boundings = graph_extent.bounds
print(boundings)

(139.6485205, 35.679703098111986, 139.76085718240986, 35.7832654)

OpenStreetMapを操作するライブラリをimportします。

import osmnx as ox
import networkx as nx
import geopandas as gpd
import matplotlib.pyplot as plt
import pandas as pd
from pyproj import CRS
import contextily as ctx

GeoDataFrameの中にデータを格納します。

place_polygon = gpd.GeoDataFrame()
place_polygon.at[0, "geometry"] = graph_extent
place_polygon.at[0, "bbox_north"] = boundings[3]
place_polygon.at[0, "bbox_south"] = boundings[1]
place_polygon.at[0, "bbox_east"] = boundings[2]
place_polygon.at[0, "bbox_west"] = boundings[0]

CRSを定義します。

# Define crs
place_polygon.crs = CRS.from_epsg(4326)
print(place_polygon.crs)

EPSG:4326

polygonから"徒歩"の地図を取得します。network_typeには徒歩の他に車など他の種別も指定可能です。

# Retrieve the network
graph = ox.graph_from_polygon(place_polygon["geometry"].values[0], network_type='walk')

地図をplotしてみます。徒歩可能な地図なので、ほぼ潰れて見えますが、よく見るとノードとエッジで地図ができていることが見て取れます。（画像の右下の方に丸と線があることが若干見て取れると思います。）

# plot the graph:
fig, ax = ox.plot_graph(graph)

地図から、ノード情報と、エッジ情報を取得します。簡単に言うとノードが建物や公園などの名称が与えれた場所を指し、エッジがそれらノードをつなぐ道と理解していただければ良いかと思います。

# Retrieve nodes and edges
nodes, edges = ox.graph_to_gdfs(graph)

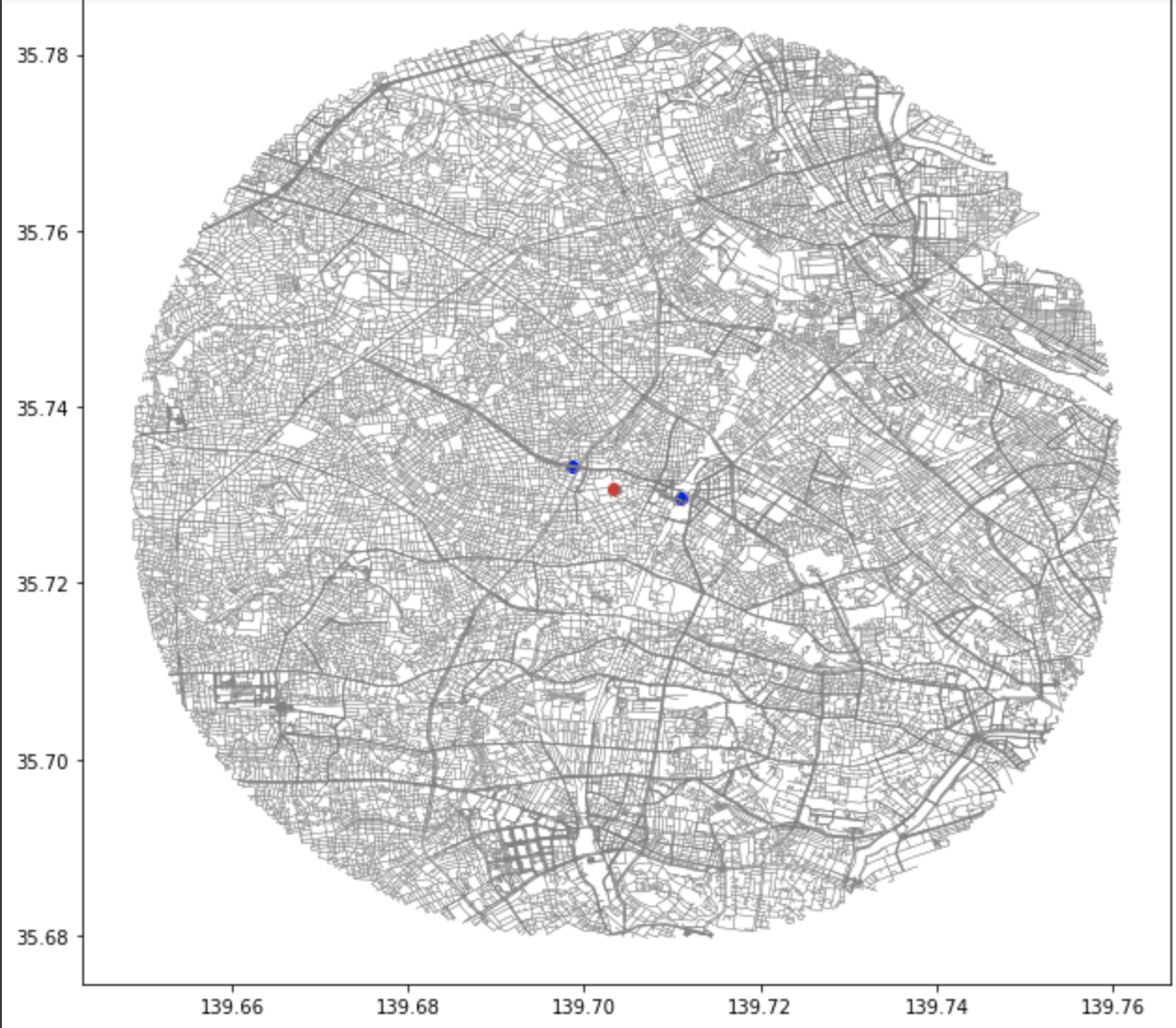
取得した地図にスタート地点とゴール地点をプロットしてみます。
スタート地点が赤、ゴール地点を青で表示します。

gdf_org = gpd.GeoDataFrame(df_org, geometry = gpd.points_from_xy(df_org.x, df_org.y))
gdf_dst = gpd.GeoDataFrame(df_dst, geometry = gpd.points_from_xy(df_dst.x, df_dst.y))

fig, ax = plt.subplots(figsize=(12,8))

# Plot street edges
edges.plot(ax=ax, linewidth=0.5, edgecolor='gray', alpha=0.7)

# Plot org
gdf_org.plot(ax=ax, facecolor='red')

# Plot dst
gdf_dst.plot(ax=ax, color='blue')

plt.tight_layout()

先程は地図情報からノードとエッジに分けて取得しました。
ノードとエッジの情報は以下のコードでも取得できます。

# Project the data
graph_proj = ox.project_graph(graph) 

# Get Edges and Nodes
nodes_proj, edges_proj = ox.graph_to_gdfs(graph_proj, nodes=True, edges=True)

CRSを定義します。

# Define crs
gdf_org.crs = CRS.from_epsg(4326)
gdf_org = gdf_org.to_crs(nodes_proj.crs)
gdf_dst.crs = CRS.from_epsg(4326)
gdf_dst = gdf_dst.to_crs(nodes_proj.crs)

標高差、地図距離を受けて、三平方の定理を用いて実距離を返す関数を定義します。

# 三角関数
def pythagoras(height, distance):
    hypotenuse =  (abs(height)**2 + abs(distance)**2)**0.5
    return hypotenuse

少し長いコードになりますが、以下のコードはやっていることは単純です。
「ox.distance.nearest_nodes(graph_proj, gdf_org.loc[i].geometry.x, gdf_org.loc[i].geometry.y)」にてその地点に一番近い地図上のノードを取得できます。
（緯度経度で指定箇所が必ず地図上でノードとして存在しているとは限りません。そのため、指定地点から一番近いノードを取得します。）
スタート地点とゴール地点のノードIDを取得します。そのID間の最短経路に含まれるノードIDを返します。
今回の例だと立教大学付近のIDは「1675516061」、池袋駅付近のIDは「7093652768」、要町駅付近のIDは「6214539149」だと分かります。
途中点のノードを取得しながら、そのノードの緯度経度情報から標高データを取得します。
更にそれらの途中点の標高差、距離から実距離を出していき、最終的にスタート地点からゴール地点までの全ての実距離を合算します。
今回の例だと立教大学から池袋駅までは合計793mほど、要町駅までは合計683mほどという結果になりました。

# 最寄りノード取得、及び最短経路取得
from shapely.geometry import LineString, Point
import warnings
warnings.simplefilter('ignore')

# ノード情報保持用データフレーム
df_org_nodes = pd.DataFrame()
df_dst_nodes = pd.DataFrame()

routes = gpd.GeoDataFrame()



for i in range(len(df_org)):
    # スタート地点最寄りノード取得
    orig_node_id = ox.distance.nearest_nodes(graph_proj, gdf_org.loc[i].geometry.x, gdf_org.loc[i].geometry.y)
    # Retrieve the rows from the nodes GeoDataFrame based on the node id (node id is the index label)
    orig_node = nodes_proj.loc[orig_node_id]
    # node情報をデータフレームに追加
    df_org_nodes = df_org_nodes.append(orig_node)

    for j in range(len(df_dst)):
        target_node_id = ox.distance.nearest_nodes(graph_proj, gdf_dst.loc[j].geometry.x, gdf_dst.loc[j].geometry.y)
        # Retrieve the rows from the nodes GeoDataFrame based on the node id (node id is the index label)
        target_node = nodes_proj.loc[target_node_id]
        # node情報をデータフレームに追加
        df_dst_nodes = df_dst_nodes.append(target_node)
        
        # Calculate the shortest path
        if orig_node_id != target_node_id:
            route = nx.shortest_path(G=graph_proj, source=orig_node_id, target=target_node_id, weight='length')           
            # Show what we have
            print("from " + str(orig_node_id) + " to " + str(target_node_id) + " : " + str(route))
            # Get the nodes along the shortest path
            route_nodes = nodes_proj.loc[route]
            # Create a geometry for the shortest path
            route_line = LineString(list(route_nodes.geometry.values))
            # print(route_line)
            routes = routes.append({"geometry":route_line}, ignore_index=True)     

            # 経路ノードをテーブル化
            df_routes = pd.DataFrame(route, columns=['node'])
            # 緯度経度列を追加
            df_routes['latitude'] = 0
            df_routes['longitude'] = 0
            # 標高列を追加
            df_routes['height'] = 0
            # 各経路ノードの標高取得
            for k in range(len(df_routes)):
                progress_node = nodes_proj.loc[df_routes.iat[k, 0]]
                
                # progress_node=[y, x, street_count, lon, lat, highway, ref, geometry]
                lat = progress_node.lat
                lon = progress_node.lon
                df_routes.iat[k, 1] = lat
                df_routes.iat[k, 2] = lon

                poi = ee.Geometry.Point([lon, lat])
                height = get_max(poi)
                df_routes.iat[k, 3] = height

            # 距離列を追加
            df_routes['distance'] = 0
            # 各経路ノードまでの距離取得
            for l in range(len(df_routes)):
                if l == 0:
                    distance = 0
                else:
                    progress = list([df_routes.iat[l, 0],df_routes.iat[l-1, 0]])
                    progress_nodes = nodes_proj.loc[progress]
                    progress_line = LineString(list(progress_nodes.geometry.values))
                    distance = progress_line.length
                df_routes.iat[l, 4] = distance
            
            # 標高考慮距離列を追加
            df_routes['hypotenuse'] = 0
            # 各経路ノードの標高考慮距離取得（各経路ノード間は直線と仮定する）
            for m in range(len(df_routes)):
                if m == 0:
                    hypotenuse = 0
                else:
                    diff_height = df_routes.iat[m, 3] - df_routes.iat[m-1, 3]
                    hypotenuse = pythagoras(diff_height, df_routes.iat[m, 4])
                    df_routes.iat[m, 5] = hypotenuse
            
            # スタートからゴールまでの合計標高考慮距離
            sum_hypotenuse = df_routes['hypotenuse'].sum()
            print('Total : ' + str(sum_hypotenuse))
        
            # 経路ノードpopup追加
            for n in range(len(df_routes)):
                folium.Marker(location=[df_routes.iat[n, 1], df_routes.iat[n, 2]], icon=folium.Icon(color="green"), popup="[" + str(df_routes.iat[n, 0]) + "] " + str(df_routes.iat[n, 1]) + "," + str(df_routes.iat[n, 2]) + " : " + "height/" + str(height) + " distance/" + str(distance)).add_to(map)

from 1675516061 to 7093652768 : [1675516061, 1675493867, 1304787368, 1093943158, 444324783, 1987943406, 444324784, 1666747652, 9944745115, 9944745118, 6225694972, 9944745120, 6450703524, 6225462371, 6225462361, 7093614728, 7093614727, 7093614729, 6225439858, 6225439861, 7093641879, 7093652769, 7093652768]
Total : 793.5944437021484
from 1675516061 to 6214539149 : [1675516061, 1304786769, 2031421737, 2022276549, 6071858655, 2022276555, 2022276554, 6071858648, 1675527858, 2031421765, 1709745714, 1709745712, 9944495997, 1075212404, 693027273, 9944495992, 9944495989, 9944496025, 6214606889, 6214539143, 6214539149]
Total : 683.9901341840892

ちなみに上記のような面倒なことをしなくてもLINESTRINGにノード情報を格納することで、そのLINESTRINGを距離換算することが可能です。
最長、最短ルートを出してみると、当然ですがどちらも上記に算出した実距離より少し短い事がわかります。

routes["route_dist"] = 0
for i in range(len(routes)):
    routes["route_dist"][i] = routes['geometry'][i].length

# 最長、最短ルートを取得
route_max = routes.loc[routes['route_dist'].idxmax()]
route_min = routes.loc[routes['route_dist'].idxmin()]
print(route_max)
print(route_min)

geometry LINESTRING (382742.71909011336 3954877.0823819...
route_dist 769.02594
Name: 0, dtype: object
geometry LINESTRING (382742.71909011336 3954877.0823819...
route_dist 674.09937
Name: 1, dtype: object

まとめ

今回は地図から取得できる距離に、標高差を加味した実際に歩く距離を算出してみました。地図アプリで取得できる距離に標高差が加味されているのかは正直わかっていません。。。
ただ、OpenStreetMap上の情報を用いて、更にそれらのデータに標高データを衛星データから付与することで地図上の情報＋衛星データを組み合わせた処理を実施できました。
OpenStreetMapだけの操作だけでも覚えることはたくさんありますが、衛星データを組み合わせることでやれる幅は更に広がりそうです。
これからも勉強しながら成果を記事にしていこうと思うので、よろしくお願いします。

参考文献

※1 ヘルシンキ大学　GIS教材
https://autogis-site.readthedocs.io/en/latest/index.html

※2　Geopandasリファレンス
https://geopandas.org/en/stable/gallery/choropleths.html