Minima Hopping法を用いて吸着構造を探索する

ASE (Atomic Simulation Environment) に実装されているMinima Hopping法を用いて，Pt表面上でのH₂分子の吸着構造を探索してみます．この記事は公式ドキュメントのチュートリアルを参考にして作成しました．

なおEMTを用いているのは計算速度上の理由によります．特に有機分子（C, H, O, N) については，公式ドキュメントで言及されているように, 単なるお遊びのモデルです．信頼性はありません．実務などで使用する場合は適切な理論を選択してください．

スラブモデルを作成

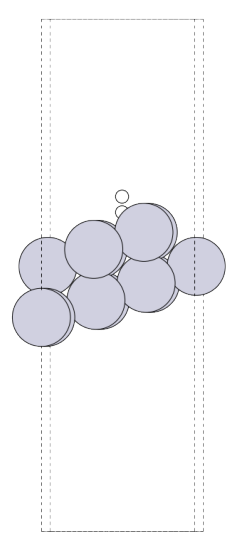
Pt (211)表面上にH₂分子を吸着させたモデルを作成します．

from ase.build import surface, add_adsorbate
from ase.data import atomic_numbers, covalent_radii
from ase.visualize import view

# Ptバルク
Pt_bulk= bulk('Pt', 'fcc', a=3.9, cubic=True) 

# Pt(211)スラブ
Pt_211 = surface(Pt_bulk, (2,1,1), 3, vacuum=10, periodic=True) 
d_PtH = (covalent_radii[atomic_numbers['H']] + covalent_radii[atomic_numbers['Pt']])
z_max =  np.max(Pt_211.positions[:,2]) # Pt原子のz座標の最大値
xy_center = ((Pt_211.cell[0]+Pt_211.cell[1])/2)[0:2]

# H2分子を追加
add_adsorbate(Pt_211, molecule('H2'), d_PtH, xy_center)

# 構造を確認
view(Pt_211)

拘束条件を設定

FixAtoms クラスと Hookean クラスを用いて，拘束条件を設定します．
Hookean の拘束条件では原子間などにバネ様の力を課します．

• Ptスラブは完全に固定する
• H₂分子は分子が壊れず，表面から離れすぎないように

from ase.calculators.emt import EMT
from ase.constraints import FixAtoms, Hookean
from ase.optimize.minimahopping import MinimaHopping

# 拘束条件
const_Pt = [FixAtoms(indices=[atom.index for atom in Pt_211 if atom.symbol=='Pt'])]
d_HH = covalent_radii[atomic_numbers['H']] * 2
H_indices = [atom.index for atom in Pt_211 if atom.symbol=='H']
const_H2 = [Hookean(a1=H_indices[0], a2=H_indices[1], rt=d_HH*1.3, k=15.), # rtは距離の閾値[A], kはバネ係数
            Hookean(a1=H_indices[0], a2=(0., 0., 1., -(z_max+d_PtH*5)), k=5.),
            Hookean(a1=H_indices[1], a2=(0., 0., 1., -(z_max+d_PtH*5)), k=5.)]
surf.set_constraint(const_Pt + const_H2)
surf.set_calculator(EMT())

Minima Hoppingを実行

Minima Hoppingを実行します．デフォルトではログはhop.logファイルに出力されます．

hop = MinimaHopping(surf, Ediff0=0.5, T0=2000)
hop(totalsteps=10)

結果の可視化

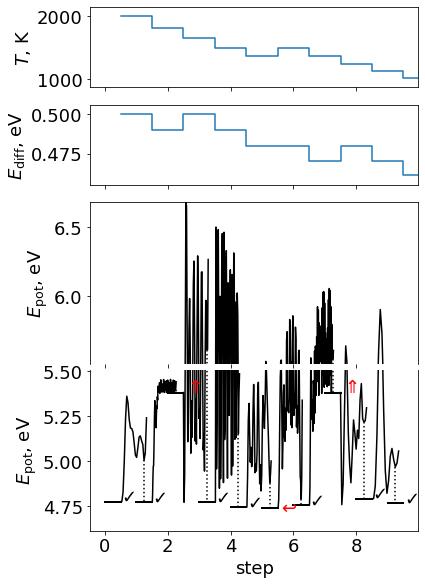
ase.optimize.minimahopping モジュールにはMinimaHoppingの結果を可視化する MHPlot 関数が実装されています. matplotlibのラッパです．
黒色のチェックマークが新規に見つかった極小構造を示します．

import matplotlib.pyplot as plt
from ase.optimize.minimahopping import MHPlot

plt.rcParams["font.size"] = 18 # 文字サイズを調整
MHPlot()

Minima Hoppingにより見つかった極小構造も確認しておきましょう．

参考

• Constrained minima hopping (global optimization) https://wiki.fysik.dtu.dk/ase/tutorials/minimahopping/minimahopping.html