UdacityのIntro to Inferential Statistics Lesson8 受講メモ

※自分用メモです。

Exact Z-Score

• 正規分布でμ（標本平均）を中心に95%になる確率分布のZ-Scoreは-1.96 +1.96
  　（Z-tableで0.025のとこ２つを見つける）

Sampling Distribution

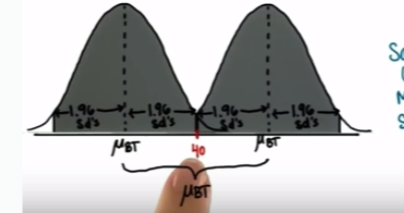
• ということで、Sampling Distributionはμから２σ両サイドに離れた（２SE：標本誤差）ところまでに95%が収まる。これは母集団でも同じ。

95% CI with Exact Z-Score

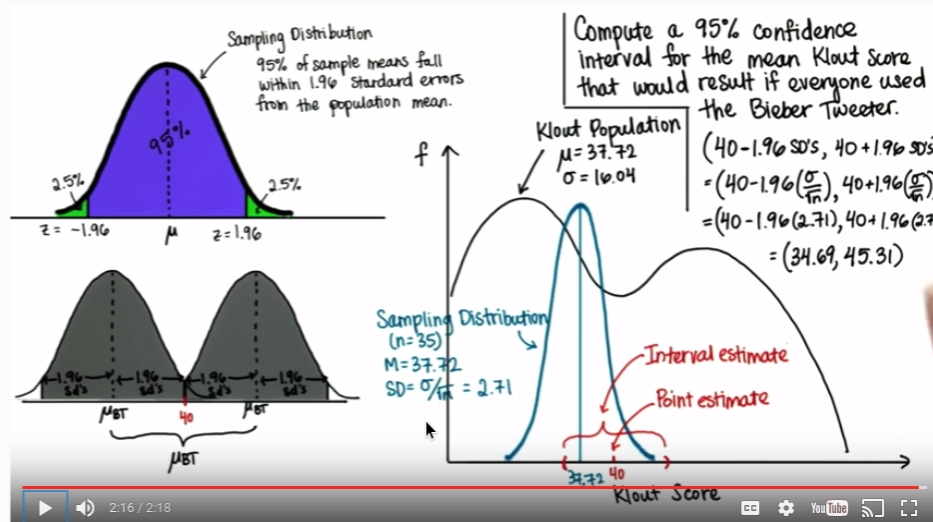
• Klout scoreで、もし、全員がBiber Twitterを使ったら、Klout scoreの平均はどの辺になるか？という問題。（タフクイズ）

解答

• まず、Sampling Distributionから、±２SE(SE=2.71)で95%が収まることは前の項で確認済。
• Population Mean（母集団平均）のKlout scoreは μ=40（これは変化させない）
• M=40からSampling DistributionのZ-scoreである、-1.96と1.96の間の確率分布が信頼できる区間ということになる。図でいうと以下。

ということで、この区間のZ-scoreを求めればOK。式は
40-1.96SD , 40+1.96SD
= 40-(1.96(σ/sqrt(n))), 40+(1.96*(σ/sqrt(n)))
= 40-(1.962.71), 40+(1.962.71)
= (34.69 , 45.31)

上記が信頼区間となる。

CI when n=250

サンプル数（n)が大きければ大きいほど、信頼区間が狭くなるという確認。
上記の確率分布でn=250だった場合、SD=σ/(sqrt(n))=1.01となる。
そのため、信頼区間は
40-(1.961.01), 40+(1.961.01) = (38.02, 41.98)となる。

Z for 98% CI

信頼区間を98%にしたい時は、Z-Scoreから取り直して再計算すればよい。

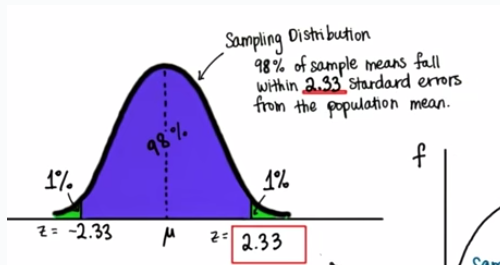
※この±2.33を98%CIのCritical Valueという。

Engagement Ratio

• Standard Deviation（標準偏差）の出し方のおさらい（STDEV* 関数でもOKなんですが、一応おさらい）

1. データ列をスプレッドシートにコピペする。
2. データ列の平均を出す。
3. データ列の隣列に分散をそれぞれのデータ分出す。((data-Mean)^2)
4. 分散の平均を出す。
5. 分散の平均に対してルートをとると、標準偏差となる。

Standard Error

Standard Error=σ/(sqrt(n))ということ。Standard DistributionとSampling ErrorとStandard Errorの区別がついてないのはご愛嬌。（ビデオもSDとSEの区別がイマイチわかりにくい・・・）

CI Bounds

• 信頼区間(CI)から予測値を算出していく。
• CIを95%としたとき、N=8702, 母集団平均=0.077, σ=0.107,の母集団 標本平均=0.13の場合の予測値を求める。
  

解答

1. 信頼区間95%の時のZ-scoreを思いだす。（Z-score = ±1.96）
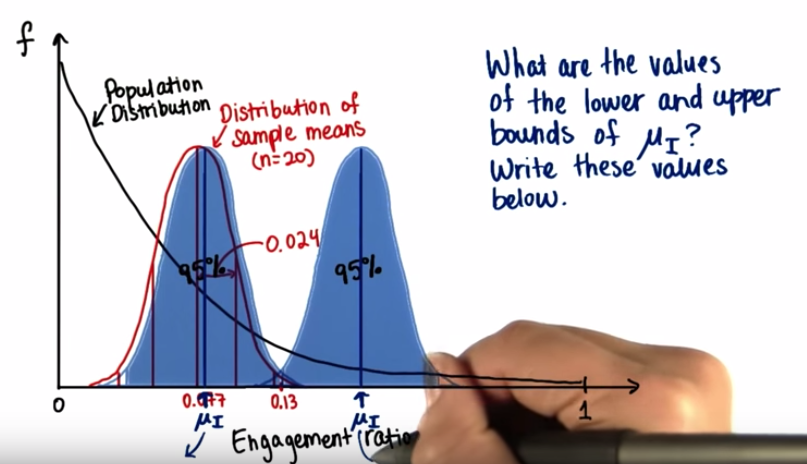
2. 標本平均=0.13なので、0.13を中心にした区間を割り出す。
3. 0.13より上は右側のμIで、0.13+1.96*(SE=0.024）=0.083
4. 同様に下側のμIは、0.13-1.96*(0.024）=0.177
5. ということで95%CI = (0.083, 0.177）

Side Note

<定義>
Engagement Ratio = Number of minutes watched / Total minutes available

• 0.083 min watched / a min availavle = 5 min watched / 60 min availavle
• 0.177 min watched / a min availavle = 10.62 min watched / 60 min availavle

95%CIで上記のように予測した。実際には６０分あたりで５分弱だったそうで予測の範囲内だった。

Margine Error

Y%の信頼区間で算出した予測値の信頼区間の半分の距離（z*σ/(sqrt(n))をMargine Errorという。

練習問題

• 標本平均 = 母集団平均
• 標準誤差 = σ / (sqrt(n))

母集団と標本集団の関係性が画像で分かる。

標本平均のZ-scoreの求め方

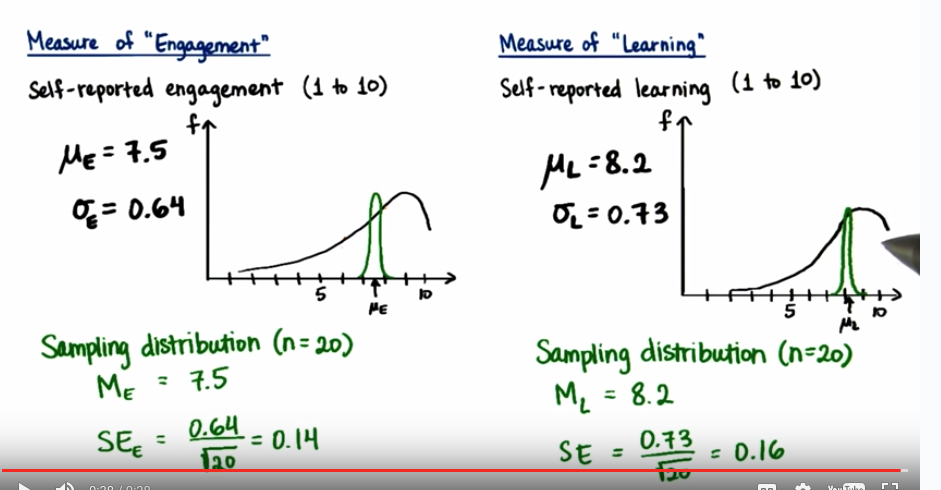
• 標本平均 Xe=8.94,Xl=8.35の時のそれぞれのZ-score
• 計算式は　（標本平均-母集団平均）/ Standard Error
  　　Ze = (8.94-7.5) / (0.64 / sqrt(20)) = 10.06
  　　Zl = (8.35-8.2) / (0.73 / sqrt(20)) = 0.92
  
  ※平均のずれをStandard Errorで割ることで、SEを基準としたズレ値を算出することができ、したがって、グラフ上に表現することが可能となる。

標本平均を超える確率

• n=20の時にXe=8.94、Xl=8.35を超える確率を求める。
• Ze / ZlのそれぞれのZ-ScoreからZ-tableで確率を求めて1から引けばOK.
  　Ze = 10.06で大きすぎるため、Z-tableからは算出できず。⇒極小
  　Zl = 0.92なので、Z-tableから0.8212が求まる。1-0.8212 = 0.18
  上記が答えとなる。

結論

• Zeが極小の確率で出ていることから、Engagementに対しては影響があると言える。
• Zlは18%の確率が出ていることから、Learningに対しては影響があるとは言えない。
  　（多分、何もしないでもランダムに２０人に対してSamplingするとこの値は出るから）
• ということで、Engagementには影響を与えるが、Learningには影響を与えない。
• また、予測なのでCausedに関しては答えがないので不正解となる。
  　(Colleration is not Causation)

Problem Set 8 Note