自粛期間が続く最中
無料マンガアプリで過去の作品が色々読めてしまうので気になってしまいました。
漫画カイジに出てきたギャンブルチンチロリンです。
カイジ
本伸行による一連の漫画作品、およびそれをもとにしたアニメおよび実写映画。
元々はダメ人間だが、危機が迫った極限の状態に置かれると並外れた度胸と才能を発揮する
主人公伊藤開司のことですが、ここでは漫画のことになります。
現在、以下の5+1篇が刊行されている。
また、スピンオフ作品として『中間管理職トネガワ』『1日外出録ハンチョウ』が存在する。
賭博黙示録カイジ(1996年-1999年 週刊ヤングマガジン、全13巻)
賭博破戒録カイジ(2000年-2004年 週刊ヤングマガジン、全13巻)
賭博堕天録カイジ(2004年-2008年 週刊ヤングマガジン、全13巻)
賭博堕天録カイジ 和也編(2009年-2012年 週刊ヤングマガジン、全10巻)
賭博堕天録カイジ ワンポーカー編(2012年‐2017年 週刊ヤングマガジン、全16巻)
賭博堕天録カイジ 24億脱出編(2017年‐連載中、既刊6巻)
基本ギャンブルをテーマとして扱った作品になっています。
チンチロリン
漫画では第三章欲望の沼編に登場するギャンブルです。
地下強制労働施設内でのレクリエーションとして大槻班長が持ちかけてきたギャンブルがこれです。
ルール
サイコロを3つ同時に振って役が揃うまで振る(最大3回まで)
お椀などにサイコロを入れて逆さまにして地面に置きお椀をとれば出目が決まります。
役は強い順で以下の通りです。
| 役名 | 条件 |
|---|---|
| ピンゾロ | 1・1・1 |
| ゾロ目 | 2・2・2 , 3・3・3 , 4・4・4 , 5・5・5 , 6・6・6 |
| シゴロ | 4・5・6 |
| 出目の大きい順番 | 2枚が同じで、残った1つの目の数 |
| ションベン | 役がなかった場合や,お椀からサイコロが出た場合 |
| ヒフミ | 1・2・3 |
漫画では払い戻しのルールなどもありますが、今回はそこは割愛して
単純に役が出る確率を考えていきます。
まずは役を判定する関数を考えてみましょう。
役は一番強いピンゾロが1、以降強い順として数値を戻す関数を作っていきます。
なおここでは振り直しも考えず、揃わなければ役なしと同じ扱いにします。
なおゾロ目はどれが出ても同じ強さと考えます。
def tintiro_hand(h):
# ピンゾロ
if all([h[0]==1,h[1]==1,h[2]==1]):
return 1
# ゾロ目
if h[0]==h[1] and h[1]==h[2]:
return 2
# シゴロ
if [4,5,6]==list(sorted(h)):
return 3
# ヒフミ
if [1,2,3]==list(sorted(h)):
return 11
# 出目 and ションベン
calc = {}
for n in h:
if n in calc:
calc[n]+= 1
else:
calc[n]=1
if 2 in calc.values():
return 3 + 7-sorted(calc.items(),key=lambda x:x[1])[0][0]
else:
return 10
def judge(h1,h_2):
if h1==h_2:
return 'DRAW'
if h1<h_2:
return 'WIN'
else:
return 'LOSE'
勝敗を判定する関数も作ります。
同じサイコロ同士で戦った場合の勝敗
import itertools
from fractions import Fraction
hands1 = list(itertools.product([1,2,3,4,5,6],repeat=3))
hands2 = list(itertools.product([1,2,3,4,5,6],repeat=3))
wins = {}
for hand1 in hands1:
for hand2 in hands2:
w = judge(tintiro_hand(hand1),tintiro_hand(hand2))
if w in wins:
wins[w] +=1
else:
wins[w] = 1
total = sum(wins.values())
draw,win,lose =wins['DRAW'],wins['WIN'],wins['LOSE']
print('DRAW\t' , Fraction(draw,total) , ' \t{:%}'.format(draw/total))
print('WIN \t' , Fraction(win ,total) , '\t{:%}'.format(win/total))
print('LOSE\t' , Fraction(lose,total) , '\t{:%}'.format(lose/total))
| DRAW | 1639/5832 | 28.10% |
|---|---|---|
| WIN | 4193/11664 | 35.95% |
| LOSE | 4193/11664 | 35.95% |
勝敗の確率は一緒です。まあ、当たり前ですよね。
シゴロ賽と対決した場合の勝敗
シゴロ賽
大槻班長が用いたイカサマサイで 4,5,6しかで目がないサイコロです。
4の裏は4と言うように、裏側が同じ数字になっているため一方向から見た時には
気づけないと言う特徴があります。
これを使うと勝率はどのように変わるのでしょうか?
普通のサイコロと勝負してみます。
import itertools
from fractions import Fraction
hands1 = list(itertools.product([1,2,3,4,5,6],repeat=3))
hands2 = list(itertools.product([4,5,6,4,5,6],repeat=3))
wins = {}
for hand1 in hands1:
for hand2 in hands2:
w = judge(tintiro_hand(hand1),tintiro_hand(hand2))
if w in wins:
wins[w] +=1
else:
wins[w] = 1
total = sum(wins.values())
draw,win,lose =wins['DRAW'],wins['WIN'],wins['LOSE']
print('DRAW\t' , Fraction(draw,total) , '\t{:%}'.format(draw/total))
print('WIN \t' , Fraction(win ,total) , '\t{:%}'.format(win/total))
print('LOSE\t' , Fraction(lose,total) , ' \t{:%}'.format(lose/total))
| DRAW | 107/1944 | 5.50% |
|---|---|---|
| WIN | 175/1944 | 9.00% |
| LOSE | 277/324 | 85.49% |
勝ち負けが同じ確率から、負けが50%増えます。素敵なサイコロですね。
役が出る確率は?
役が出る確率は、まずサイコロの組み合わせが216通り($6^3$)なのでこれが分母になります。
それぞれのサイコロでの役の確率を見てみると
import itertools
import matplotlib.pyplot as plt
%matplotlib inline
hands1 = list(itertools.product([1,2,3,4,5,6],repeat=3))
hands = {}
for hand1 in hands1:
h = tintiro_hand(hand1)
if h in hands:
hands[h] +=1
else:
hands[h] = 1
plt.figure(figsize=(12,6))
x = [k for k,v in sorted(hands.items())]
y = [v for k,v in sorted(hands.items())]
for x1,y1 in zip(x,y):
plt.text(x1, y1+1 , y1 , size = 10, color = "green")
plt.text(x1, y1+10 , '{:.01%}'.format(y1/216), size = 10, color = "black")
label = ['111','ゾロ目','シゴロ','6','5','4','3','2','1','ションベン','123']
plt.bar(x,y,tick_label=label)
plt.grid()
plt.show()
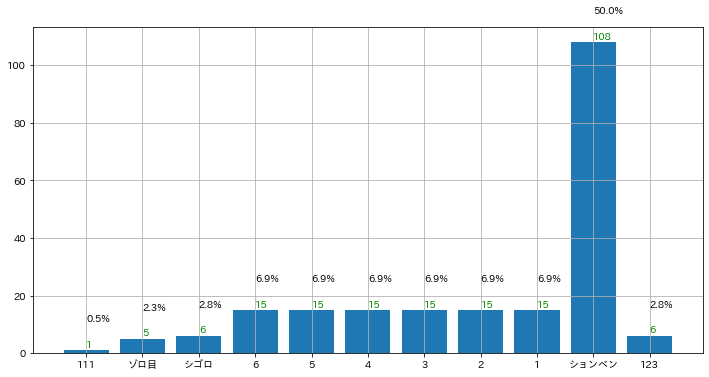
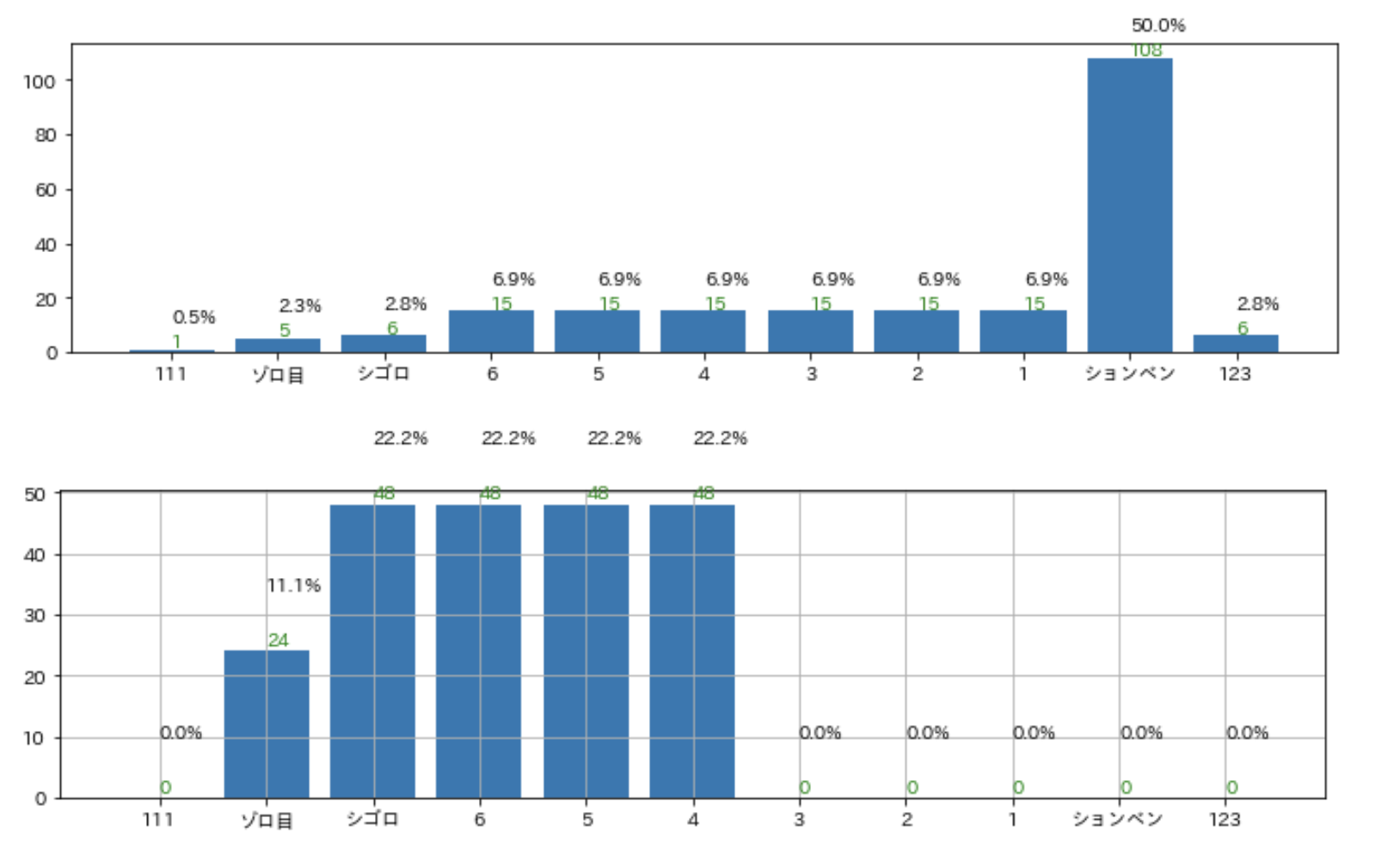
三回振り直しを考慮せず、確定したものとすると一番出る役は役なし(ションベン)です。
だから3回振り直しっていうルールなのかもねと思います。
ピンゾロは1通りしかありません。一番弱い123は6通り存在します。
これがシゴロ賽だとどうなるでしょうか?
import itertools
import matplotlib.pyplot as plt
%matplotlib inline
hands = list(itertools.product([4,5,6,4,5,6],repeat=3))
hands2 = {i:0 for i in range(1,12)}
for hand in hands:
h2 = tintiro_hand(hand)
if h2 in hands2:
hands2[h2] +=1
else:
hands2[h2] = 1
plt.figure(figsize=(12,6))
x = [k for k,v in sorted(hands2.items())]
y = [v for k,v in sorted(hands2.items())]
for x1,y1 in zip(x,y):
plt.text(x1, y1+1 , y1 , size = 10, color = "green")
plt.text(x1, y1+10 , '{:.01%}'.format(y1/216), size = 10, color = "black")
label = ['111','ゾロ目','シゴロ','6','5','4','3','2','1','ションベン','123']
plt.bar(x,y,tick_label=label)
plt.grid()
plt.show()
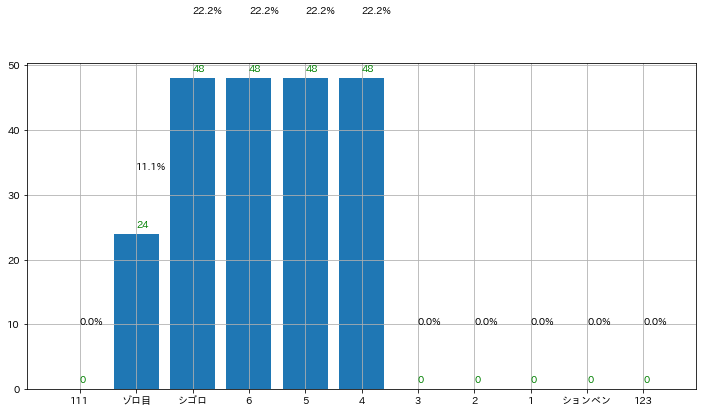
なーんか圧倒的ですね。
シゴロ賽であれば、役がないことが無くなり最低でも4がでます。
ゾロ目の確率は5倍弱、シゴロの確率は8倍ですね。
漫画だと111の払いを高めて456の払いをやや弱くしたりして、カモフラージュしていたりとか
色々画策していてルールが面白くなってます。
イカサマを見つけるには
このイカサマサイコロの仕組みを見破ったのは、同僚の三好がつけていた出目の記録です。
班長の此処一番の勝負の時だけ、やけに456が多いなと言うところに気付き
イカサマサイコロの存在を疑うようになります。
通常のサイコロであれば、456の確率は3%弱なので、100回に2-3回しか出ないことになります。
続ければ続けるほど確率は収束し、本来の確率に近づくはずなので
何千回とデータをとり続ければ、確率のおかしさに気がつけるかもしれません。
日々のデータ取得や確率の気付きは大切ですねーーー
まとめ
やはりギャンブルに勝つには統計や確率が改めて重要だとと言うことがわかるかと思います。
IRの事もあり公的な機関がもしチンチロリンを開催するようになったら
こう行ったイカサマも流行るかも知れませんし、その時を楽しみにしたいですね。
作者の情報
乙pyのHP:
http://www.otupy.net/
Youtube:
https://www.youtube.com/channel/UCaT7xpeq8n1G_HcJKKSOXMw
Twitter:
https://twitter.com/otupython