U-TOKYO AP Advent Calendar 2017
物理工学科っぽいネタかつQiitaに載せても良さそうな話題ということで、強相関電子系の模型に対する厳密対角化に関して紹介します。
強相関電子系とは
強相関電子系とは、通常の金属やバンド絶縁体と比べて、電子間の相互作用が強い物質のことを指します。
代表的な例としては、モット絶縁体や銅酸化物高温超伝導体などが挙げられます。
また、電子間の相互作用が本質的に重要であることに起因して、理論的な取り扱いが非常に難しいことが知られています。
ハバード模型
典型的な強相関電子系の格子模型として、ハバード模型があります。
以下のような第二量子化された(=生成消滅演算子で書かれた)ハミルトニアンで記述されます。
H=-t\sum_{<i,j>} (c_i^\dagger c_j + c_j^\dagger c_i ) + U\sum_i n_{i\uparrow} n_{i\downarrow}
$c_i$は$i$番目のサイトの消滅演算子、$c_i^\dagger$は$i$番目のサイトの生成演算子です。
$< i,j >$は、$i$番目のサイトと$j$番目のサイトが隣接しているもののみ和をとることを意味します。
第一項目の$t$の項は強束縛模型と同じで、電子がサイト$i$とサイト$j$の間を飛び移ることでエネルギーの利得を得る効果を表しています。
第二項目は同じサイトに2つの電子がいるとクーロン斥力$U$だけエネルギーを損する(エネルギーが上がってしまう)効果を表しています。
ハバード模型を解くのは難しい
ハバード模型は一見単純そうに見えますが、実は解くのが非常に難しいです。その理由を述べます。
生成消滅演算子をフーリエ変換することで波数$k$の電子に対する生成消滅演算子を定義することができます。
$t$の項は、波数$k$の生成消滅演算子$c_k^\dagger , c_k$を用いて定義できる波数空間基底に対して対角となります($\sum_{k\sigma} \epsilon(k) c_{k\sigma}^\dagger c_{k\sigma} $のように書ける)。
一方、$U$の項は、実空間基底に対して対角となっています。
$t$の項だけなら波数空間基底で、$U$の項だけなら実空間基底でハミルトニアンを表現すれば対角行列となりますが、両者の和に関してはハミルトニアンを対角化するような基底は簡単には求まりません。
波数空間基底でも実空間基底でも「良い基底」ではないということ、これが強相関電子系の難しいところです。
そこで厳密対角化
ハバード模型のような強相関電子系の模型の素朴な解析方法として、有限サイズの系に対してハミルトニアンを行列表示して、それを数値的に対角化するという方法が挙げられます。
これが厳密対角化です(より厳密に厳密対角化について述べておくと、多くの場合は基底状態か、もしくは基底状態まわりの低エネルギー励起状態しかまず求めることはありません)。
例えば、1次元格子のハバード模型に対してサイト数(格子点の数)を10個に制限すると、実空間基底でハミルトニアンを有限次元の行列で表すことができます。
厳密対角化のメリット
物理的な近似を一切しておらず、計算結果は正確です。
厳密対角化のデメリット
系のサイズが小さいものしか計算できません。
fillingにもよりますが、普段使っているPC程度では14サイト~18サイトあたりが限界でしょう。
その原因は、行列の次元が系のサイズに対して指数関数的に増大することにあります。
サイト数が$L$個だとすると、それぞれのサイトには「電子がいない」「アップスピンの電子のみがいる」「ダウンスピンの電子のみがいる」「二重占有が生じている」という4通りの状態があります。
そのため、系全体の状態としては$4^L$通りの状態があるわけです。
実際には系全体でのアップスピンの電子数とダウンスピンの電子数が等しい基底のみを集めてくるので$4^L$よりはひどいことにはなりませんが、それでも指数関数的に増大します。
その結果、計算量、必要なメモリの両方が系のサイズに対して指数関数的に増大します。
一方で現実の系はサイト数が非常に多く、ほぼ無限サイズと見なせます。
小さなサイズの系だから生じてしまう効果のことを有限サイズ効果と呼びますが、この有限サイズ効果は非常に深淵な問題です。
それでも厳密対角化は有用!
厳密対角化以外にも計算手法はいくつかありますが、どの手法にもメリット・デメリットがあります。(1次元以外の計算は難しいとか、負符号問題とか……)
厳密対角化は他と比べると実装は比較的容易で、他の手法の計算結果が正しいか判断するためにも使うことができます。
また、基底状態に関する静的な物理量だけでなく、一粒子励起スペクトル(実験的にはARPESやIPESに対応)や光学伝導度といった、動的な物理量も簡単に計算できます。
さらには、シュレディンガー方程式に基づいて時間発展を計算することで、非平衡な光励起状態を計算することもできます。
計算の手順
行列表示
実空間基底でハミルトニアンを行列表示します。
ハミルトニアン行列のサイズはサイト数に対して指数関数的ですが、一方で非零の要素数はサイト数程度のオーダーですので、ハミルトニアン行列は零の値ばかりの行列(疎行列)となります。
そのため、非零の値の部分のみをデータとして格納します。
ランチョス法による三重対角化
エルミートな疎行列の固有値問題の計算手法として、物理に限らず一般にランチョス法が有用です。
ランチョス法の計算コストの多くは行列ベクトル積の部分で、行列ベクトル積では行列中の非零の要素のみを計算すれば良いので、疎行列向けの計算手法となっています。
これにより、対称な三重対角行列へと変換します。
基底状態を求める場合、このときの三重対角行列のサイズは、およそ100次元程度で十分な精度となります(たった100次元程度で基底状態が求まる原理としては、べき乗法で行列ベクトル積を計算するたびに絶対値最大の固有値に対応する固有状態が増幅されることと同じで、この三重対角行列には基底状態の成分が十分に含まれています)。
三重対角行列の対角化
三重対角行列であることに拘る必要はなく、通常の密行列の対角化をすれば良いです。
私はLAPACKを使っています。
三重対角行列であることを利用して、スツルムの定理と二分法を用いた方法で固有値を求めてから固有状態を求める人もいます。
基底状態を用いて様々な量を計算
静的な物理量としては、例えば基底状態における隣接サイト間のスピン相関$< S_i \cdot S_{i+1}>$(<>は基底状態での期待値)を計算して隣接スピン間で磁気的な秩序があるかを調べたりできます。
光学伝導度のような動的な物理量に関しては、線形応答理論(久保公式)を用いて計算します。
このとき、$< O^\dagger (\omega + E_o - H + i\eta)^{-1} O >$($O:演算子、E_0:基底状態のエネルギー、\eta:正の微小量$)のような物理量を求める必要がありますが、これはランチョス法の応用で求めることができます。
詳しくは『計算物理III ―数値磁性体物性入門―』http://www.asakura.co.jp/books/isbn/978-4-254-13715-6/ を読むと良いでしょう。
少しマイナーな話:光励起による非平衡状態の計算
基底状態を求めた後、その基底状態を初期状態として、光励起による非平衡状態の時間発展を求めることができます。
光の効果に関しては、トランスファー$t$にパイエルス位相をかけることで取り入れることができます。
$t \rightarrow t e^{-iA(\tau)}$ ($A(\tau):時刻\tauにおけるベクトルポテンシャル$)のような感じです。
時間発展に関しては、シュレディンガー方程式より、$\psi(\tau + \delta \tau) \simeq \exp(-iH(\tau)\delta \tau)\psi(\tau)$のように求めることができます。
右辺に関しては、ランチョス法の応用で求めることができます。
光励起後の状態に対して光学伝導度を計算したりすることもできます(実験的にはポンプ・プローブ分光に対応します)。
終わりに
実際にコードを組む時には、上で挙げた本を読むなり、ネットに落ちている修論・博論を参考にするなりするとよいと思います。(私がコードを組む時には、東北大理学系研究科物理学専攻の修論・博論も参考にしていました)
これを機に厳密対角化erが増えたりしたら幸いです。
追記
Qiitaらしく計算結果も載せておいた方が良いとのことだったので、最近行った追計算を一応載せておきます。
追計算した論文はSatoshi Miyashita et al., J. Phys. Soc. Jpn. 79, 034708 (2010)
(http://journals.jps.jp/doi/abs/10.1143/JPSJ.79.034708 )のFig. 3. (b)です。
JPSJの論文が読めない人向け:arXivのプレプリント https://arxiv.org/abs/0912.4850
$\mathrm{\alpha-(BEDT-TTF)_2I_3}$という、異方的な二次元三角格子3/4-filledの有機導体に対する計算です。
この物質は低温でhorizontal stripeと呼ばれるジグザグの電荷秩序が実現しており、不均一な電荷分布が生じています。
また、低温相は対称性が悪く、自発分極が生じています(電子型強誘電体)。
この系には等価でない4つのサイトがあり、それらをA,A',B,Cとしています。
この系に対し、光励起した後の各サイトの電荷量の時間発展を求めています。
模型は、ハバード模型に隣接サイト間のクーロン斥力$V$の項を加え、さらにインターサイトの分子サイト間距離の変化の効果をトランスファー$t$の変調として取り入れた模型(拡張パイエルス・ハバード模型)です。
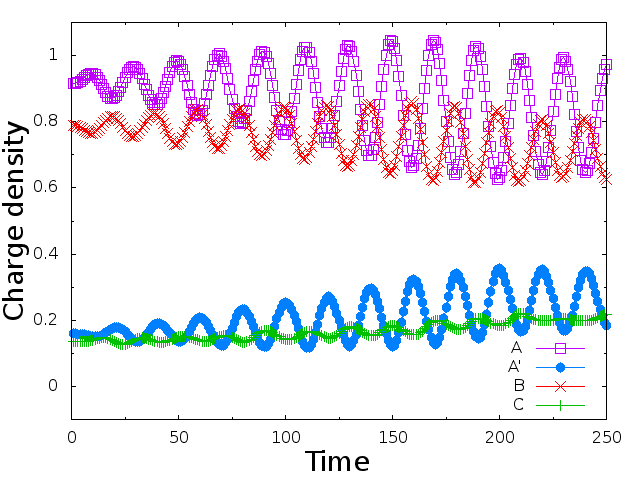
詳しくは論文を読んでください。
ソースコードは人様に見せられる状態ではないので公開する予定はありません。
追記
HΦという厳密対角化のパッケージがありますが、最近になって時間発展計算にも対応したようです。
MateriApps Live!を導入すれば簡単に使えるはずなので、気になった人は試してみてはいかがでしょうか。