ウイルス感染をシミュレーション→「SIRモデル」
現在日本では、コロナウイルスの感染が広がっている。ウイルス感染のシミュレーションを行うのに、「SIRモデル」というのがよく使用されるそうだ。今回は、他の方の資料を参考にMatlabを用いてSIRモデルを解いてみたのでまとめてみた。
参考にさせてもらったサイト
荻田 武史、捕食・被食関係のシミュレーション
荻田 武史、感染症流行のシミュレーション
捕食者と被食者の方程式の求解
SIRモデルとは
S :未感染者の人数(Susceptible)
I :感染者の人数(Infected)
R :亡くなったまたは回復した人数(Recovered)
全人口をS、I、Rの三つに分けて、初期条件と適切なパラメーターを選択して微分方程式を解くことで、時間とともに変化する感染人数をシミュレーションできる。
ここでS、I、Rは時間tの関数である。
微分方程式
\frac{dS(t)}{dt} = -βS(t)I(t)\\
\qquad\quad\frac{dI(t)}{dt}= βS(t)I(t)-γI(t)\\
\frac{dR(t)}{dt}= γI(t)\qquad\\
\\
\ β:感染率[1/日]\\
\ γ:回復率[1/日]\\
これを解くことで、シミュレーションすることができる。
プログラミング(Matlab)
「SIR_sim.m」という名前でファイルを作成する。
function dy = SIR_sim(t,y)
a = 0.001; % β感染率[1/日]
b = 0.5; % γ回復率(隔離率)[1/日]
dy = zeros(3,1);
dy(1) = -a*y(1)*y(2);
dy(2) = a*y(1)*y(2)-b*y(2);
dy(3) = b*y(2);
実行
Matlabのコマンドラインから次のコマンドを実行する。
>> t = [0,200]
>> y0= [1000;1;0]
>> [t,y]=ode45('SIR_sim',t,y0);
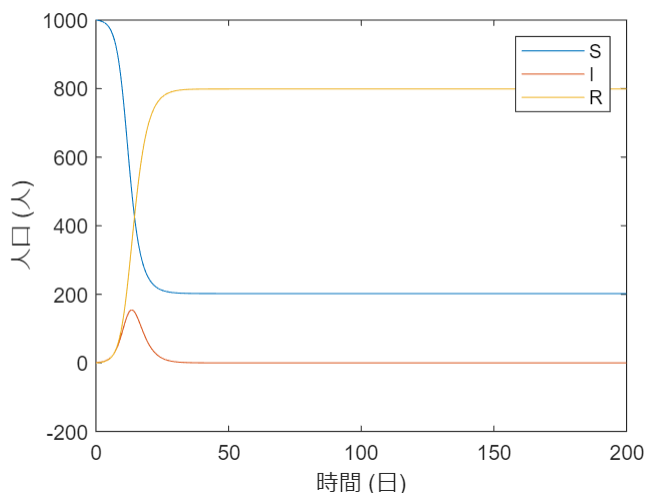
>> plot(t,y)
>> xlabel('時間 (日)')
>> ylabel('人口 (人)')
>> legend('S','I','R')
プログラム内の β、γ、時間を表す t、初期条件 y0を変更することでシミュレーションすることが可能である。今回実行した値は適当に決めた値で根拠はない。
おわりに
Matlabを用いてSIRモデルを簡単にシミュレーションすることができた。