C#で立体を描く簡易的なプログラム
前回の記事で投稿したプログラムがいろいろと間違っていたので、修正しました。
ライブラリなど使えば簡単にできると思いますが、やはりここは、全て自作です!
立体を描くクラス
G3D.cs
using System;
using System.Drawing;
using System.Windows.Forms;
namespace _3D
{
class G3D
{
private Bitmap canvas;
private Graphics g;
private PictureBox pictureBox;
private double x_adj, y_adj;
private double x_theta = 0, y_theta = 0, z_theta = 0;
public G3D(PictureBox p)
{
pictureBox = p;
canvas = new Bitmap(p.Width, p.Height);
g = Graphics.FromImage(canvas);
x_adj = p.Width / 2;
y_adj = p.Height / 2;
}
public void cuboid(double x1, double y1, double z1, double x2, double y2, double z2, double x_rot_theta, double y_rot_theta, double z_rot_theta)
{
double x_rot = x_theta;
double y_rot = y_theta;
double z_rot = z_theta;
Point[] p = { point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta,x1, y1, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x2, y1, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta,x2, y2, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta,x1, y2, z1) };
g.DrawPolygon(Pens.White, p);
Point[] p1 = { point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta,x2, y1, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta,x2, y2, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta,x2, y2, z2),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x2, y1, z2) };
g.DrawPolygon(Pens.White, p1);
Point[] p2 = { point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta,x1, y1, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x1, y2, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x1, y2, z2),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta,x1, y1, z2)};
g.DrawPolygon(Pens.White, p2);
Point[] p3 = { point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x1, y1, z2),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x2, y1, z2),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x2, y2, z2),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x1, y2, z2)};
g.DrawPolygon(Pens.White, p3);
Point[] p4 = { point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x1, y1, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x2, y1, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x2, y1, z2),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x1, y1, z2)};
g.DrawPolygon(Pens.White, p4);
Point[] p5 = { point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x1, y2, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x2, y2, z1),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x2, y2, z2),
point_culc(x_rot, y_rot, z_rot, x_rot_theta,y_rot_theta,z_rot_theta, x1, y2, z2)};
g.DrawPolygon(Pens.White, p5);
g.DrawLine(Pens.DarkRed,
point_culc(x_theta, y_theta, z_theta, x_rot_theta, y_rot_theta, z_rot_theta, ((x1 + x2) / 2) + 50, (y1 + y2) / 2, (z1 + z2) / 2),
point_culc(x_theta, y_theta, z_theta, x_rot_theta, y_rot_theta, z_rot_theta, (x1 + x2) / 2, (y1 + y2) / 2, (z1 + z2) / 2)
);
g.DrawLine(Pens.DarkGreen,
point_culc(x_theta, y_theta, z_theta, x_rot_theta, y_rot_theta, z_rot_theta, (x1 + x2) / 2, ((y1 + y2) / 2) + 50, (z1 + z2) / 2),
point_culc(x_theta, y_theta, z_theta, x_rot_theta, y_rot_theta, z_rot_theta, (x1 + x2) / 2, (y1 + y2) / 2, (z1 + z2) / 2)
);
g.DrawLine(Pens.LightYellow,
point_culc(x_theta, y_theta, z_theta, x_rot_theta, y_rot_theta, z_rot_theta, (x1 + x2) / 2, (y1 + y2) / 2, ((z1 + z2) / 2) + 50),
point_culc(x_theta, y_theta, z_theta, x_rot_theta, y_rot_theta, z_rot_theta, (x1 + x2) / 2, (y1 + y2) / 2, (z1 + z2) / 2)
);
}
public void clear()
{
g.Clear(Color.Black);
}
public void draw()
{
g.DrawLine(Pens.Red,
point_culc(x_theta, y_theta, z_theta, 0, 0, 0, 100, 0, 0),
point_culc(x_theta, y_theta, z_theta, 0, 0, 0, 0, 0, 0)
);
g.DrawLine(Pens.Green,
point_culc(x_theta, y_theta, z_theta, 0, 0, 0, 0, 100, 0),
point_culc(x_theta, y_theta, z_theta, 0, 0, 0, 0, 0, 0)
);
g.DrawLine(Pens.Yellow,
point_culc(x_theta, y_theta, z_theta, 0, 0, 0, 0, 0, 100),
point_culc(x_theta, y_theta, z_theta, 0, 0, 0, 0, 0, 0)
);
pictureBox.Image = canvas;
}
public void camera_change(double rotx,double roty,double rotz)
{
x_theta = rotx;
y_theta = roty;
z_theta = rotz;
theta_lim(ref x_theta);
theta_lim(ref y_theta);
theta_lim(ref z_theta);
}
public void camera_step(double rotx, double roty, double rotz)
{
x_theta += rotx;
y_theta += roty;
z_theta += rotz;
theta_lim(ref x_theta);
theta_lim(ref y_theta);
theta_lim(ref z_theta);
}
private void theta_lim(ref double t)
{
if (t > 360)
{
t -= 360;
}
if (t < 0)
{
t = 360 + t;
}
}
/// <summary>
/// 回転後のポイント計算
/// </summary>
/// <param name="rotx">X軸周りでの回転角度(視点)</param>
/// <param name="roty">Y軸周りでの回転角度(視点)</param>
/// <param name="rotz">Z軸周りでの回転角度(視点)</param>
/// <param name="f_rotx">X軸周りでの回転角度(図形)</param>
/// <param name="f_roty">Y軸周りでの回転角度(図形)</param>
/// <param name="f_rotz">Z軸周りでの回転角度(図形)</param>
/// <param name="x">X座標</param>
/// <param name="y">Y座標</param>
/// <param name="z">Z座標</param>
/// <returns></returns>
private Point point_culc(double rotx, double roty, double rotz, double f_rotx, double f_roty, double f_rotz, double x, double y, double z)
{
double rad = Math.PI / 180;
//図形の回転
//X軸周りで回転
double X_x = x * 1;
double Y_x = y * Math.Cos(f_rotx * rad) - z * Math.Sin(f_rotx * rad);
double Z_x = y * Math.Sin(f_rotx * rad) + z * Math.Cos(f_rotx * rad);
//Y軸周りで回転
double X_y = X_x * Math.Cos(f_roty * rad) + Z_x * Math.Sin(f_roty * rad);
double Y_y = Y_x * 1;
double Z_y = -X_x * Math.Sin(f_roty * rad) + Z_x * Math.Cos(f_roty * rad);
//Z軸周りで回転
double X_z = X_y * Math.Cos(f_rotz * rad) - Y_y * Math.Sin(f_rotz * rad);
double Y_z = X_y * Math.Sin(f_rotz * rad) + Y_y * Math.Cos(f_rotz * rad);
double Z_z = Z_y * 1;
//視点の回転
double X_ = Math.Cos(roty * rad) * Math.Cos(rotz * rad) * X_z
- Math.Cos(roty * rad) * Math.Sin(rotz * rad) * Y_z
+ Math.Sin(roty * rad) * Z_z;
double Y_ = (Math.Sin(rotx * rad) * Math.Sin(roty * rad) * Math.Cos(rotz * rad) + Math.Cos(rotx * rad) * Math.Sin(rotz * rad)) * X_z
+ (-Math.Sin(rotx * rad) * Math.Sin(roty * rad) * Math.Sin(rotz * rad) + Math.Cos(rotx * rad) * Math.Cos(rotz * rad)) * Y_z
- Math.Sin(rotx * rad) * Math.Cos(roty * rad) * Z_z;
return new Point((int)(X_ + x_adj), (int)(Y_ + y_adj));
}
}
}
今回は、視点の回転、図形そのものの回転をできるようにしました。
前回は視点の回転のみだったんですが、視点を変えると言うことは、3次元座標自体も回転しないといけません。
例えばX軸周りに回転させた場合Y軸とZ軸も傾きます。
そこのプログラムがちょっとまずかったので、直しました。
図形そのものの回転をしたときの座標を計算するプログラムは、前回の視点の回転をしたときの座標を計算するプログラムと同じです。
そこのところを誤解してしまったようです。
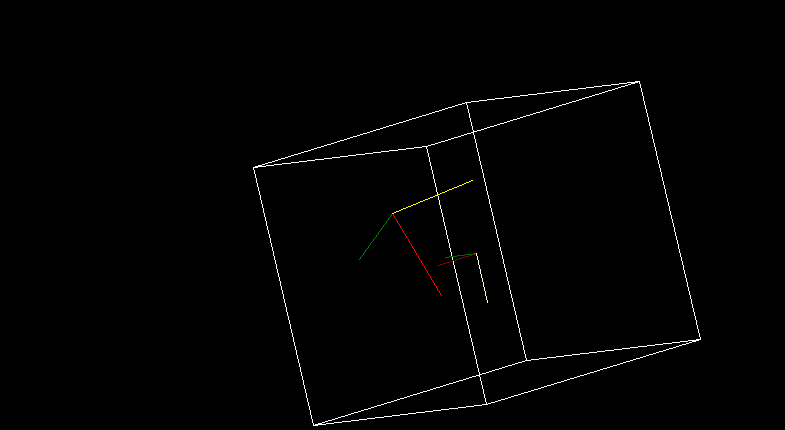
実行結果
真ん中の赤緑黄は、3次元空間上のX軸Y軸Z軸を表しています。
小さく赤緑黄で表示されているのは、表示されている立体の元のX軸Y軸Z軸を表しています。
視点だけではなく、立体そのものも回転させているため、3次元空間上の3軸と、立体の元の3軸は向きが一致していません。