「隣のトイレを使わないでっ！」 最大で何人が同時にトイレを使えるか考えてみよう

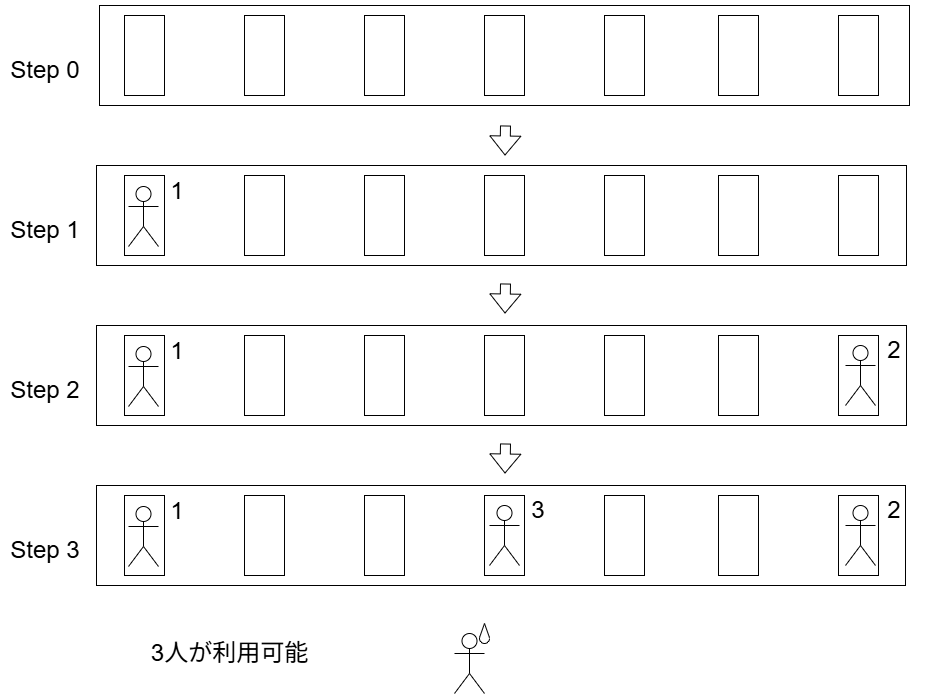
皆さんはトイレを使用するときに、既に利用する人がすぐ隣にいるトイレを使用するのを避け、何個か空けてトイレを利用することはありませんか？　そんなことから着想を得て思いついた次の問題について、本記事では考えてみます。

この記事で扱う問題

この建物には$N$個のトイレがあります。しかしこの街の住人は恥ずかしがりやで、既にトイレを利用している人がいる場合には、他の人から最も遠いトイレを選んで利用します。また他の人が既に利用している隣のトイレを利用することはできません。最初の人が最適なトイレを選んだ場合に、最大で何人のユーザが同時にトイレを利用することができるでしょうか。

経緯

私は男子トイレを利用しますが、小便器と個室のどちらを利用する場合でも、隣に人がくると少し緊張しています。また、私からはあまり人が利用している隣のトイレを選ぶことはありません。このように感じる方は意外と多いのではないでしょうか。どうやら海外の方でも同じように感じる方もいるようです。

そこでこの行動を次のようなルールに落とし込んだ問題について、検討することにします。

• 人が利用しているトイレがある場合には、他の人から最も遠いトイレを利用する
• 人が使用している隣のトイレしか空いていない場合には、トイレの利用をあきらめる

このようなルールを設定した場合に、最大で何人のユーザが使用できるのでしょうか。
また、どのような傾向があるのかを検討していきます。これを競技プログラミング風の問題文にしたのが、記事の先頭に記載した問題です。

具体的な例

例えば次の図のような$5$個のトイレがある例を考えてみます。

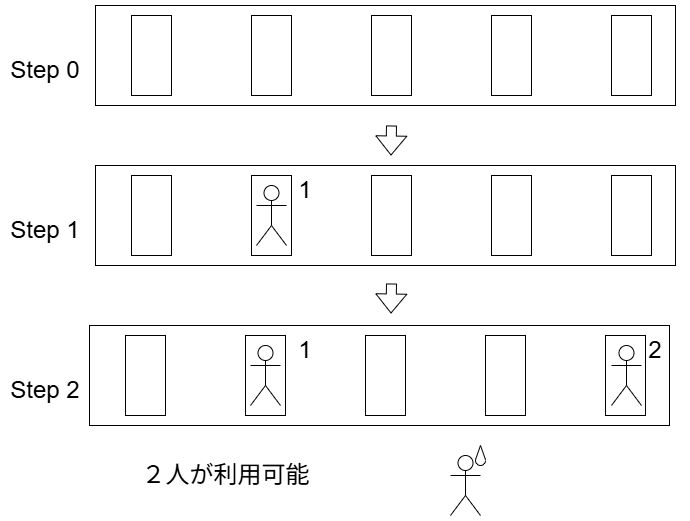
この例では、最初の$1$人が左から$2$番目のトイレを利用しました。次に$2$人目が最も離れた右側のトイレを利用します。そうすると、残りの$3$つの空きトイレはいずれも利用中のユーザの隣になるため、利用することができません。

しかし最初の$1$人が別の場所を選ぶと、異なる結果となります。最初の$1$人が最も左のトイレを選んだとします。

この例では、$2$人目が最も右のトイレを選び、$3$人目が真ん中のトイレを利用できます。このように最初の$1$人が選んだ場所により、利用できるユーザの数が変わってくることがわかります。この記事では 最初のユーザが選んだトイレをFirst Position(FP)と呼ぶことにします。 しかし最初のユーザが端のトイレを選べば必ずしも良いわけではなく、次のような例ではうまくいきません。

Step$3$で$3$人目のユーザが真ん中のトイレを利用しますが、この場合は4つのデッドスペースが生じてしまいます。

$7$個のトイレがある場合には、例えば左から$3$番目のトイレから使い始めると、うまくいきます。

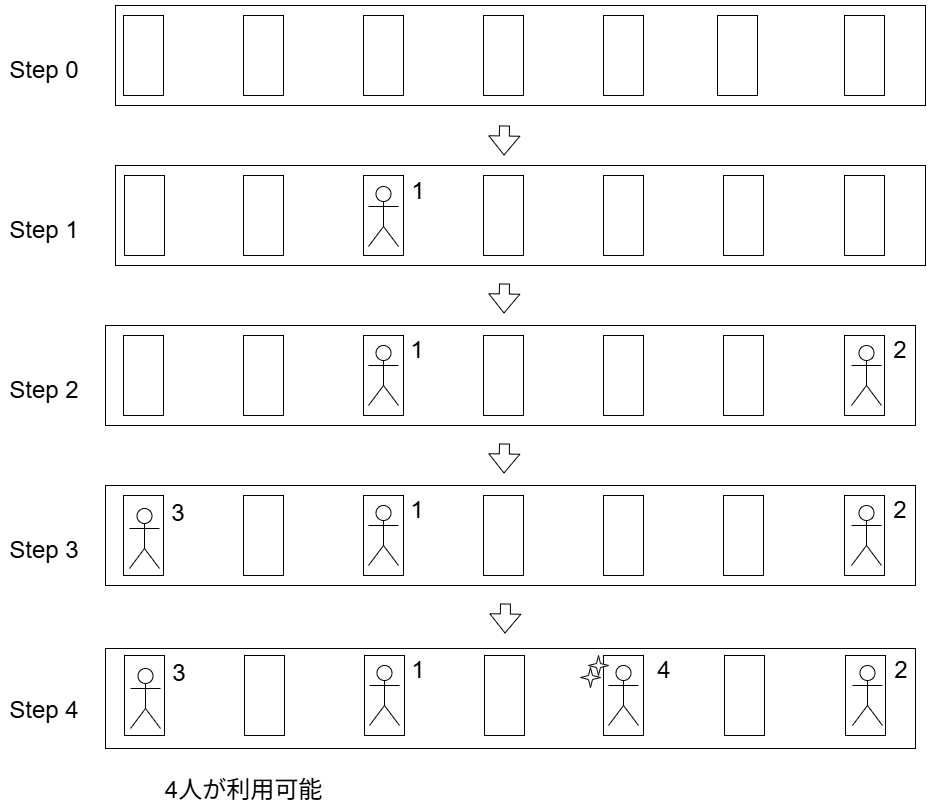
トイレが奇数個で、すべての奇数番目のトイレが埋まった場合には、利用率が$0.5$を超えます。また偶数個のトイレでは利用できるトイレがすべて埋まった場合には、利用率が$0.5$になります。

簡単な実装

まずは簡単なプログラムを作成し、$N$個のトイレと最初のユーザが使うトイレの番号(左端が$1$、右端が$N$となります)を指定します。どのようにトイレが埋まっていくかを可視化するプログラムです。

━━━━━━━━━━━━━━━━━━╮
┃    ソースコードを表示（折りたたみ）   ┃
╰━━━━━━━━━━━━━━━━━━╯

N_FP_set.py

import time

DEFMAX = 999999

def main():
    # パラメータ入力
    print("How many toilets are there?")
    N = int(input())
    print("What number do you use?")
    firstUser = int(input())

    if (firstUser > N) or (firstUser < 1):
        print("can not choise")
        return

    print("-----------------------------")

    startTime = time.time()

    # N個の便器を生成
    toilets = [0] * N
    print_now(toilets)
    # 最初のトイレを使用中にする
    toilets[firstUser-1] = 1
    print_now(toilets)

    while True:
        # 現在何人が使用しているか
        nowPerson = max(toilets)
        leftbox = [0] * N
        leftCount = DEFMAX
        rightbox = [0] * N
        rightCount = DEFMAX
        for i in range(N):
            #左側から探索
            if toilets[i] == 0:
                leftCount += 1
            else:
                leftCount = 0
            leftbox[i]=leftCount
            #右側から探索
            if toilets[-1-i] == 0:
                rightCount += 1
            else:
                rightCount = 0
            rightbox[-1-i]=rightCount

        #今回使う便器を選択
        priorotyBox = [0]*N
        for i in range(N):
            priorotyBox[i] = min(leftbox[i], rightbox[i])
        if max(priorotyBox) < 2:
            break
        nowPerson += 1
        # 便器の情報を更新
        toilets[priorotyBox.index(max(priorotyBox))] = nowPerson
        print_now(toilets)

    endTime = time.time()
    timeDiff = endTime-startTime

    print("-----------------------------")
    print(f"use person : {max(toilets)}")
    print(f"utilization rate : {round(max(toilets)/N, 5)}")
    print(f"time:{round((timeDiff), 4)}[s]")


def print_now(toilets):
    now = max(toilets)
    print(f"{now:4}: ", end="")
    for i in range(len(toilets)):
        if (toilets[i] == now) and (now != 0):
            print("|x", end="")
        elif (toilets[i] != 0):
            print("|o", end="")
        else:
            print("| ", end="")
    print("|")


if __name__ == "__main__":
    main()

$7$個のトイレの$3$番目を利用した出力は以下のようになります。

How many toilets are there?
7
What number do you use?
3
-----------------------------
   0: | | | | | | | |
   1: | | |x| | | | |
   2: | | |o| | | |x|
   3: |x| |o| | | |o|
   4: |o| |o| |x| |o|
-----------------------------
use person : 4
utilization rate : 0.57143
time:0.0003[s]

出力例には0～4の行がありますが、これが上の例のStepを意味します。そのステップで埋まったトイレを"x"で、既に埋まっているトイレを"o"で示しています。縦に見ると、"x"で埋まったトイレは、その後も"o"となり利用し続けています。

この例では最初に3番目を利用し(FP)、次のStep2で右端のトイレが埋まります。そうして4Stepで計4人が利用できます。また利用率は$4/7=0.57143$となります。

しかしこの実装は計算量が$O(N^2)$になるため、あまり早くありません。例えば$N=1024$の場合には、FirstPosition一つ試行するのに私のPCでは$0.35$秒要しました。FirstPositionは$1$から$N/2$まで試したいので、$N$が大きい場合には、計算コストが大きいです。

傾向の確認

それでもこのコードを拡張し、$1$から$N$までのトイレの数の各場合の、最適なFirstPositionを選んだ場合の最大利用可能者数を計算するコードを総当りで作成しました。なお、このコードは、最低な選び方をした場合の最小利用可能者数も併せて出力します。

━━━━━━━━━━━━━━━━━━╮
┃    ソースコードを表示（折りたたみ）   ┃
╰━━━━━━━━━━━━━━━━━━╯

N_range_set.py

import time

DEFMAX = 999999

def main():
    # パラメータ入力
    print("Chceck range?")
    N = int(input())

    startTime = time.time()
    for i in range(1,N+1):
        checkN(i)
    endTime = time.time()
    timeDiff = endTime-startTime

    print("-----------------------------")
    print(f"time:{round((timeDiff), 4)}[s]")

def checkN(N):
    highRate = 0.0
    highUser = 0
    highFirst = 0
    lowRate = 1.0
    lowUser = 0
    lowFirst = 0
    for i in range(1,(N//2)+2):
        currentUser,currentRate = calcUtilizationRate(N, i)
        currentRate = round(currentRate, 8)
        if highRate < currentRate:
            highRate = currentRate
            highUser = currentUser
            highFirst = i
        if lowRate > currentRate:
            lowRate = currentRate
            lowUser = currentUser
            lowFirst = i
    print("-------------------------------------")
    print(f"{N} MAX SCORE firstPosition:{highFirst} user:{highUser}, Rate:{highRate}")
    print(f"{N} MIN SCORE firstPosition:{lowFirst} user:{lowUser}, Rate:{lowRate}")


def calcUtilizationRate(N,X):
    # N個の便器を生成
    toilets = [0] * N
    # 最初のトイレを使用中にする
    toilets[X-1] = 1

    while True:
        # 現在何人が使用しているか
        nowPerson = max(toilets)
        leftbox = [0] * N
        leftCount = DEFMAX
        rightbox = [0] * N
        rightCount = DEFMAX
        for i in range(N):
            #左側から探索
            if toilets[i] == 0:
                leftCount += 1
            else:
                leftCount = 0
            leftbox[i]=leftCount
            #右側から探索
            if toilets[-1-i] == 0:
                rightCount += 1
            else:
                rightCount = 0
            rightbox[-1-i]=rightCount

        #今回使う便器を選択
        priorotyBox = [0]*N
        for i in range(N):
            priorotyBox[i] = min(leftbox[i], rightbox[i])
        if max(priorotyBox) < 2:
            break
        nowPerson += 1
        # 便器の情報を更新
        toilets[priorotyBox.index(max(priorotyBox))] = nowPerson
    
    return max(toilets), max(toilets)/N #usePerson, utilizationRate



if __name__ == "__main__":
    main()

$N=100$を指定した場合の出力例の抜粋です。

Chceck range?
100
-------------------------------------
1 MAX SCORE firstPosition:1 user:1, Rate:1.0
1 MIN SCORE firstPosition:0 user:0, Rate:1.0
-------------------------------------
2 MAX SCORE firstPosition:1 user:1, Rate:0.5
2 MIN SCORE firstPosition:1 user:1, Rate:0.5
-------------------------------------
3 MAX SCORE firstPosition:1 user:2, Rate:0.66666667
3 MIN SCORE firstPosition:2 user:1, Rate:0.33333333
-------------------------------------
：
(略)
：
-------------------------------------
98 MAX SCORE firstPosition:33 user:49, Rate:0.5
98 MIN SCORE firstPosition:2 user:33, Rate:0.33673469
-------------------------------------
99 MAX SCORE firstPosition:33 user:49, Rate:0.49494949
99 MIN SCORE firstPosition:2 user:34, Rate:0.34343434
-------------------------------------
100 MAX SCORE firstPosition:33 user:49, Rate:0.49
100 MIN SCORE firstPosition:4 user:34, Rate:0.34
-----------------------------
time:1.4839[s]

$N=1024$を指定した場合に、$1$から$N$個までのトイレ数の最大利用可能者数の計算には、私のPCで17,000秒ほど要しました。

全部示すのは大変なので、そのうち$N=128$までの、最適なFirstPositionを選んだ場合の同時利用可能数と利用率を、表に示します。

N	FirstPosition	同時利用可能	利用率
1	1	1	1
2	1	1	0.5
3	1	2	0.66666667
4	1	2	0.5
5	1	3	0.6
6	1	3	0.5
7	3	4	0.57142857
8	1	4	0.5
9	1	5	0.55555556
10	1	5	0.5
11	3	6	0.54545455
12	3	6	0.5
13	5	7	0.53846154
14	5	7	0.5
15	1	7	0.46666667
16	1	8	0.5
17	1	9	0.52941176
18	1	9	0.5
19	3	10	0.52631579
20	3	10	0.5
21	5	11	0.52380952
22	5	11	0.5
23	5	11	0.47826087
24	8	12	0.5
25	9	13	0.52
26	9	13	0.5
27	9	13	0.48148148
28	9	13	0.46428571
29	1	13	0.44827586
30	1	14	0.46666667
31	1	15	0.48387097
32	1	16	0.5
33	1	17	0.51515152
34	1	17	0.5
35	3	18	0.51428571
36	3	18	0.5
37	5	19	0.51351351
38	5	19	0.5
39	5	19	0.48717949
40	8	20	0.5
41	9	21	0.51219512
42	9	21	0.5
43	9	21	0.48837209
44	9	21	0.47727273
45	9	21	0.46666667
46	14	22	0.47826087
47	15	23	0.4893617
48	16	24	0.5
49	17	25	0.51020408
50	17	25	0.5
51	17	25	0.49019608
52	17	25	0.48076923
53	17	25	0.47169811
54	17	25	0.46296296
55	17	25	0.45454545
56	17	25	0.44642857
57	1	25	0.43859649
58	1	26	0.44827586
59	1	27	0.45762712
60	1	28	0.46666667
61	1	29	0.47540984
62	1	30	0.48387097
63	1	31	0.49206349
64	1	32	0.5
65	1	33	0.50769231
66	1	33	0.5
67	3	34	0.50746269
68	3	34	0.5
69	5	35	0.50724638
70	5	35	0.5
71	5	35	0.49295775
72	8	36	0.5
73	9	37	0.50684932
74	9	37	0.5
75	9	37	0.49333333
76	9	37	0.48684211
77	9	37	0.48051948
78	14	38	0.48717949
79	15	39	0.49367089
80	16	40	0.5
81	17	41	0.50617284
82	17	41	0.5
83	17	41	0.4939759
84	17	41	0.48809524
85	17	41	0.48235294
86	17	41	0.47674419
87	17	41	0.47126437
88	17	41	0.46590909
89	17	41	0.46067416
90	26	42	0.46666667
91	27	43	0.47252747
92	28	44	0.47826087
93	29	45	0.48387097
94	30	46	0.4893617
95	31	47	0.49473684
96	32	48	0.5
97	33	49	0.50515464
98	33	49	0.5
99	33	49	0.49494949
100	33	49	0.49
101	33	49	0.48514851
102	33	49	0.48039216
103	33	49	0.47572816
104	33	49	0.47115385
105	33	49	0.46666667
106	33	49	0.46226415
107	33	49	0.45794393
108	33	49	0.4537037
109	33	49	0.44954128
110	33	49	0.44545455
111	33	49	0.44144144
112	33	49	0.4375
113	1	49	0.43362832
114	1	50	0.43859649
115	1	51	0.44347826
116	1	52	0.44827586
117	1	53	0.45299145
118	1	54	0.45762712
119	1	55	0.46218487
120	1	56	0.46666667
121	1	57	0.47107438
122	1	58	0.47540984
123	1	59	0.4796748
124	1	60	0.48387097
125	1	61	0.488
126	1	62	0.49206349
127	1	63	0.49606299
128	1	64	0.5

利用率が0.5を超える場合

最適なFirstPositionを選んだ場合の、利用率が$0.5$より大きい数値を太字で示しました。$0.5$より高いスコアを抜粋すると下記になります。

$1,2,3,5,7,9,11,13,17,19,21,25,33,35,37,41,49,65,67,69,73,81,97$

このスコアは次の2パターンに分けることができます。

パターン① $N=2^X+1$である
例:
$2=2^0+1$
$5=2^2+1$
$17=2^4+1$ など
いずれもFirstPositionが1(端)になる。

パターン② パターン①$2個-1$の形式である
例:
$7=3+5-1 = (2^1+1)+(2^2+1)-1$
$13=5+9-1 = (2^2+1)+(2^3+1)-1$
$19=3+17-1 = (2^1+1)+(2^4+1)-1$
FirstPositionの位置で分割すると、その左右がパターン①となる。

このことから利用率が$0.5$を超えるような(奇数個のトイレで奇数番目がすべて埋まる)場合は、奇数の中でも$2^X+1$かその組み合わせで表せるトイレの場合に、適切なFirstPositionのトイレが存在します。

利用率が0.5に等しい

利用率が0$.5$となるのは偶数個のトイレで、半分のトイレがすべて埋まっている場合です。これは上の$128$までの表を確認すると、上述のパターン①もしくはパターン②の$\pm1$の個数のトイレの場合に、$0.5$になることが分かります。

例：
$16 = 17-1$ 　※$17$はパターン①
$22 = 21+1$ 　※$21$はパターン②

利用率が0.5未満

このパターンには、トイレの数を$N$個とした場合に$N$の前後での利用率が$(>0.5)$のトイレの数から探索できます。

例えば$N=29$を考えてみましょう。その前後を抜粋しました。

N	FirstPosition	同時利用可能	利用率
25	9	13	0.52
26	9	13	0.5
27	9	13	0.48148148
28	9	13	0.46428571
29	1	13	0.44827586
30	1	14	0.46666667
31	1	15	0.48387097
32	1	16	0.5
33	1	17	0.51515152

$N=29$の前後で利用率が$0.5$より大きくなるのは、$N=25$および$N=33$です。

まずは$29$より低い$N=25$から近づくアプローチを確認します。$N=26,27,28$はFirstPositionの位置は9番目、同時利用可能数も13で$N=25$と変わりません。これはFirstPositionの$9$を含む左側は$5$人が利用できることは変わらず、FirstPositionの右側ではいずれの$N$でも$8$人が利用できます。しかし、使えないデッドスペースが$1$個ずつ増えていきます。

以下に、$25$から$29$までのトイレの個数の場合に、FirstPositionを$9$と固定し、最終的に埋まったトイレの配置を示します。なお最初のユーザを"fp"、埋まったトイレを"o"で示しています。

N=25:|o| |o| |o| |o| |fp| |o| |o| |o| |o| |o| |o| |o| |o|

N=26:|o| |o| |o| |o| |fp| |o| |o| |o| |o| |o| |o| |o| | |o|

N=27:|o| |o| |o| |o| |fp| |o| |o| |o| | |o| |o| |o| |o| | |o|

N=28:|o| |o| |o| |o| |fp| |o| |o| |o| | |o| |o| | |o| |o| | |o|

N=29:|o| |o| |o| |o| |fp| |o| | |o| |o| | |o| |o| | |o| |o| | |o|

トイレが$25$個の場合には、奇数番目が全て埋まっていますが、$26$から一つずつ増加するに連れて、使えないトイレが増えていくのが分かります。

逆に$29$より大きい$N=33$から近づくアプローチを考えます。この範囲ではFirstPositionは$1$固定です。これもまず図示してみます。

N=29:|fp| | |o| |o| |o| | |o| |o| |o| | |o| |o| |o| | |o| |o| |o|

N=30:|fp| | |o| |o| |o| | |o| |o| |o| | |o| |o| |o| |o| |o| |o| |o|

N=31:|fp| | |o| |o| |o| |o| |o| |o| |o| | |o| |o| |o| |o| |o| |o| |o|

N=32:|fp| | |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o|

N=33:|fp| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o| |o|

この範囲では、$N=33$から見て、トイレの数が一つずつ小さくなるに連れて、2個ならんだ空きトイレが増えていくことが分かります。なお、着目した$N=29$は、$N=25$の下からのアプローチと$N=33$の上からのアプローチの結果の利用できるユーザが$13$人でどちらでも同じ結果になります。PythonスクリプトではFirstPositionが若い方を優先したため、表ではFirstPositionが$1$の結果を表に記載しました。

なお、参考までに「FirstPositionが$1$の$N=28$」と「FirstPositionが$9$の$N=30$」出力してみます。

「FirstPositionが$1$の$N=28$」の場合

N=28:|fp| | |o| | |o| | |o| |o| |o| | |o| |o| |o| | |o| |o| |o|

結果：$12$人利用可能(利用率：0.42857)
よって、FirstPositonが$9$の場合には13人が利用可能なので、こちらのほうが低い。

「FirstPositionが$9$の$N=30$」の場合

N=30:|o| |o| |o| |o| |fp| |o| | |o| |o| | |o| |o| | |o| | |o| | |o|

結果：$13$人が利用できる。(利用率：0.43333)
よって、FirstPositonが$1$の場合には14人が利用可能なので、こちらのほうが低い。

このように、結果の$N=29$の前後での、FirstPosition選択の妥当性を確認できました。

最大の利用率の計算アルゴリズムの見直し

ここまでの分析で、トイレの数$N$に対して、最大の利用率と適切なFirstPositionの探索方法がわかりました。そこでループ探索ではなく、次のようなコードを実装しました。

• 入力$N$に対し、$N=2^X + 1$であれば、$\frac{N}{2} + 1$人が利用できる（パターン①）
  　この時FirstPositionは1になる

• 入力$N$に対し、パターン①２つの重ね合わせである
  　　$N=(2^X + 1) + (2^Y+1)-1$の場合にも、$\frac{N}{2} + 1$人が利用できる（パターン②）
  　このときFirstPositionはパターン①の重なる部分になる。

• パターン①およびパターン②の前後のトイレ数の場合には、$\frac{N}{2}$人が利用できる（パターン③）
  　このときFirstPositionは、前後のパターン①or②の位置と同じ

• それ以外の$N$の場合は、近くのパターン①または②の位置から、計算する

この方針で実装したコードが下記です。

━━━━━━━━━━━━━━━━━━╮
┃    ソースコードを表示（折りたたみ）   ┃
╰━━━━━━━━━━━━━━━━━━╯

Range_MAX_Calc.py

import itertools
import time

NMAX = 99999

def main():
    # パラメータ入力
    print("How many toilets are there?")
    N = int(input())

    start_time = time.time()
    for i in range(1, N+1):
        calc(i)
    end_time = time.time()
    timeDiff = end_time - start_time
    print("------------------------------------------")
    print(f"time:{round((timeDiff), 4)}[s]")


def calc(N):
    list2n_plus1 = []

    count = 1
    while True:
        list2n_plus1.append(2**count + 1)

        if list2n_plus1[-1] > NMAX:
            break
        count+=1

    ic = itertools.combinations(list2n_plus1, 2)
    list_make2_2n = []
    for key in ic:
        now2_2n = key[0]+key[1]-1
        if now2_2n <= NMAX:
            list_make2_2n.append([now2_2n, key[0]])
    list_make2_2n.sort()

    if N <= 2: # N=2以下
        user = 1
        fp = 1
    elif N in list2n_plus1: # Nが2のべき乗+1 ptn1
        user = N//2+1
        fp = 1
    elif N in [x[0] for x in list_make2_2n]: #[Nが2のべき乗+1]の和 ptn2
        user = N//2+1
        indexes = [i for i, x in enumerate(list_make2_2n) if x[0] == N]
        fp = list_make2_2n[indexes[0]][1]
    elif (N in [x+1 for x in list2n_plus1]): #ptn1の+1
        user = N//2
        fp = 1
    elif (N in [x-1 for x in list2n_plus1]): #ptn1の-1
        user = N//2
        fp = 1
    elif (N in [x[0]+1 for x in list_make2_2n]):#ptn2の+1
        user = N//2
        indexes = [i for i, x in enumerate(list_make2_2n) if x[0] == N-1]
        fp = list_make2_2n[indexes[0]][1]
    elif (N in [x[0]-1 for x in list_make2_2n]): #ptn2の-1
        user = N//2
        indexes = [i for i, x in enumerate(list_make2_2n) if x[0] == N+1]
        fp = list_make2_2n[indexes[0]][1]-1
    else:#それ以外
        for i in range(len(list2n_plus1)):
            if list2n_plus1[i] >= N:
                ptn1_high = i
                ptn1_low = i-1
                break
                
        for i in range(len(list_make2_2n)):
            if list_make2_2n[i][0] >= N:
                ptn2_high = i
                ptn2_low = i-1
                break
        
        #ptn1とptn2で近いスコアを探す
        #低い方からの探索は必ずptn2
        if list_make2_2n[ptn2_low][0] <= list2n_plus1[ptn1_low]:
            lowuser = list2n_plus1[ptn1_high]//2+1
            lowfp = 1
            if(N==15):
                print("x")
        else:
            lowuser = list_make2_2n[ptn2_low][0]//2+1
            lowindexes = [i for i, x in enumerate(list_make2_2n) if x[0] == list_make2_2n[ptn2_low][0]]
            lowfp = list_make2_2n[lowindexes[0]][1]

        #高い方からの探索
        if list2n_plus1[ptn1_high] < list_make2_2n[ptn2_high][0]:
            diff = list2n_plus1[ptn1_high] - N
            highuser = list2n_plus1[ptn1_high]//2+1-diff
            highfp = 1
        else:
            diff = list_make2_2n[ptn2_high][0] - N
            highuser = list_make2_2n[ptn2_high][0]//2+1 - diff
            highindexes = [i for i, x in enumerate(list_make2_2n) if x[0] == list_make2_2n[ptn2_high][0]]
            highfp = list_make2_2n[highindexes[0]][1] - diff
            if(N==15):
                print("z")
        
        if (highuser==lowuser) and (highfp==1):
            user = highuser
            fp = highfp
        elif highuser<=lowuser:
            user = lowuser
            fp = lowfp
        else:
            user = highuser
            fp = highfp

    rate = round(user/N,8)
    print(f"{N},{fp},{user},{rate}")   

if __name__ == "__main__":
    main()

このコードで$N=1$から$1024$をまとめて計算したところ 0.1258 秒で計算することができました。元の実装だと17,000秒ほど要していたので、かなり改善しました。また計算結果のFirstPositionおよび利用者数数、利用率も、一致することを確認しています。

$N=10000$でも 1.2978秒で計算できています。なお、より大きい値を計算したい場合には、最大値と仮置きした定数NMAXをもっと大きい値に変更してください。

おまけ

ここまでの検討では多くの人が利用できるパターンについて分析しました。
反対に少しの人だけが利用できる（=反対に多くの人が利用できなくなる）FirstPositionを選んだ場合、どうなるのかを考えてみます。計算結果図示します。

横軸がトイレの数$N$です。左目盛りの縦軸(青)が最小を選ぶ場合のFirstPositionで、赤線の右目盛りが同時利用可能な（最小）利用者数です。

構造に着目すると青線のFirstPositionはフラクタルな周期構造が表れていることがわかります。青が1に戻る$N$は以下のようになります。
$N=2,4,6,11,21,41,81,161,321,641$
それぞれ-1すると、
$1,3,5,10,20,40,80,160,320,640$
となり、$5$以降は、倍々で増えていることがわかります。各周期で現れる山は回を追うごとに高くなっており、各山の右上の点は同じ縮尺にした最小利用者数の赤線と重なることがわかります。

山の頂点部分などFirstPositionが変わらない(横線の)部分では赤線の利用者数が増え、FirstPositionが増える(傾きが急な)領域では、赤線の利用者が増えずに平らである関係があることがわかります。

少ない利用者しか利用できないようなFPの選び方は、一般化まではできていないですが、このような傾向があるごとがわかりました。

最後に

こんな記事ですが、最後まで読んでいただき、ありがとうございます。
何かお気づきの点がありましたら、コメントなど大歓迎です。

トイレを選ぶときには、なるべく多くの人が利用できるような場所を、積極的に選んで生きていきます。