強化学習(森村哲郎 著)を読んだ時のノート。強化学習初心者なので、これから勉強する人の参考になれば幸いです
1.3 方策
方策は行動Aを選ぶルールのことです。ルールはどんな条件の時にどの行動を選びますかという書き方になっていて、条件は、その時の状態だったり、過去の状態だったり、今まで選んできた行動だったりします。また、行動の選び方も、「一つの行動だけを選ぶ」という方法や「行動$A_1$を20%、行動$A_2$を80%の確率で選ぶ」みたいなのもあります
定常な決定的マルコフ方策
- 定常: どの時間ステップでも同じ方策
- 決定的: ある条件に対して1つの行動が対応する
- マルコフ方策: 条件として現在の状態だけを用いる
という方策です。例1.1であがっている方策の例A,B,C,Dがこれに当たります。現在の状態で行動が決まるので、方策は次の図の表の各行のどこに1を置くかで定義できます。
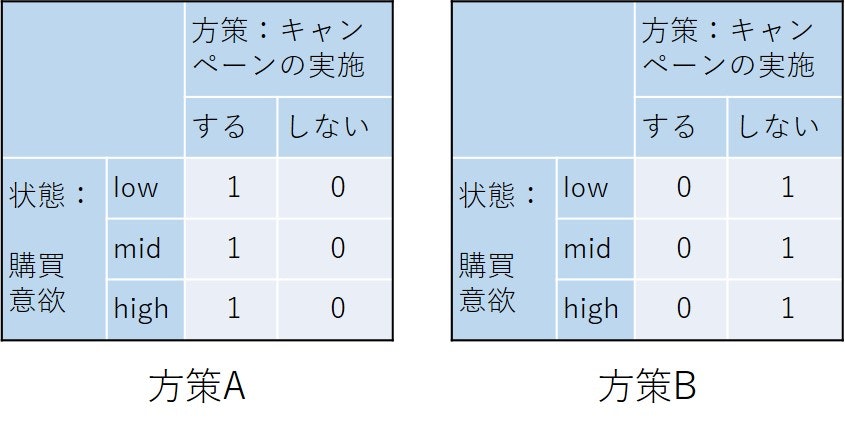
- 方策A: すべての状態でキャンペーンを実施する
- 方策B: すべての状態でキャンペーンを実施しない
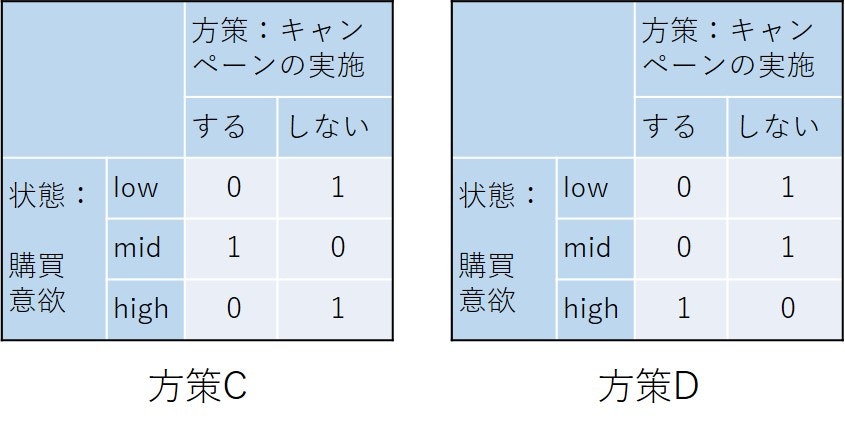
- 方策C: mid状態でキャンペーンを実施する
- 方策D: high状態でキャンペーンを実施する
上の図の中の表は例1.1で示されたA,B,C,Dの4つの方策のそれぞれを表の形で表現したものです。一つの状態を示す各行にはどこか1か所だけ「1」が入ります。0, 1のパターンが一つでも違うと違う方策となります。
定常的な方策は、下の図のようにどの時間ステップでも同じ方策を用います
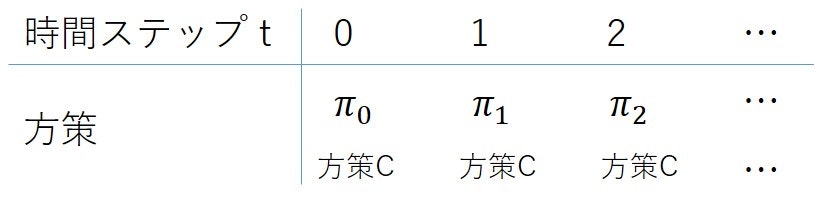
この方策のサイズ(方策集合の要素数、異なる方策の数)は、各状態で“する”/“しない”の2通り、状態の数が3なので
|A|^{|S|}=2^3
となります
非定常な決定的マルコフ方策
時間ステップ長$T$
- 非定常: 時間ステップによって方策が異なる
- 決定的: ある条件に対して1つの行動が対応する
- マルコフ方策: 条件として現在の状態だけを用いる
定常な場合との違いは、時間ステップによって異なる方策をとることなので、たとえば例1.1では以下のような、時間ステップ毎に別の方策をとれることになります。
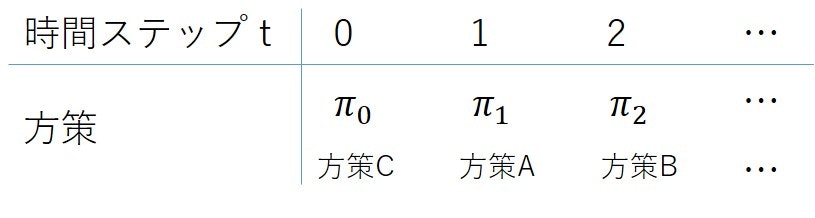
それぞれの方策がある時間ステップでの状態だけで決まることは定常の時と変わらないので、時間ステップ0の方策のサイズは定常の時と同じ$2^3$。時間ステップ1では時間ステップ0,1の方策表の組み合わせで、一つでも1の場所が異なれば異なる方策なので、$2^3\times2^3$となり、タイムステップ$T$でも同様に
(|A|^{|S|})^{|T+1|}=(2^3)^{|T+1|}
となります。
非定常で決定的、履歴依存の方策
時間ステップ長$T$
- 非定常: 時間ステップによって方策が異なる
- 決定的: ある条件に対して1つの行動が対応する
- 履歴依存の方策: 条件として履歴(過去の状態や行動)も用いる
時間ステップが3で行動を選ぶ方策の例を次に示します
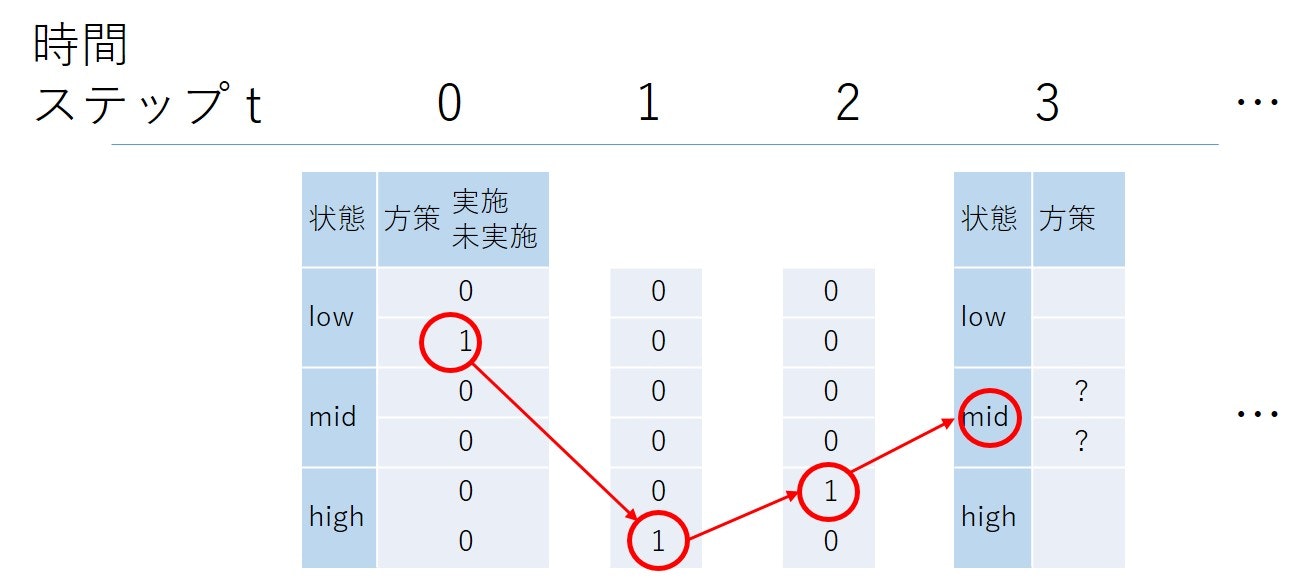
この履歴ではt=0では状態はlowでキャンペーンは未実施でした。t=1でhigh状態に遷移しキャンペーンは未実施でした。t=2でhigh状態に留まりキャンペーンを実施して、t=3でmid状態です。この一つの履歴に対し、行動はキャンペーンを実施“する”/“しない”の2通りあります。
t=3における履歴の場合の数は、履歴上のそれぞれの時間ステップでの状態と行動の組み合わせ($|S||A|=3\times2$)の時間ステップの数の組み合わせ($(|S||A|)^{T}=(3\times2)^3$)と現在の状態の数($|S|=3$)の組み合わせとなります。結局、履歴の場合の数は
|H_t|=|S|^{T+1}|A|^T=3^4\times2^3
となります。
ある一つの方策とはすべての履歴パターンに行動$|A|=2$のどれかを割り当てた表のようなもののことで、ある一つの方策の例を次に示します

一つの履歴に対する行動が違っても別の方策なので、t=3の時間ステップでの割り当てのパターンの数は
|A|^{|H_t|}=|A|^{|S|^{T+1}|A|^T}=2^{3^4\times2^3}
あり、時間ステップ$T$までのすべての履歴x行動のパターンの組み合わせは各時間ステップでのパタンの組み合わせになるので、結局時間ステップ$3$での方策のサイズは
\prod_{t=0}^T{|A|^{|S|^{T+1}|A|^T}}=2^{3^1\times2^0}\times2^{3^2\times2^1}\times2^{3^3\times2^2}\times2^{3^4\times2^3}
となります。
命題1.1
命題のイメージ
**環境は「マルコフ決定過程」
方策1)履歴依存の方策で状態sになり、かつ、行動aを選ぶ確率
の方策を決めたとすると
方策2)状態sになり、かつ、行動aを選ぶ確率が1)と同じになるマルコフ方策
を作ることができる。
それで、マルコフ方策を作る方法が式(1.16)です。
これは不思議です。下の左の図に示すように、履歴依存の方策では同じ状態sであっても、その状態までの履歴によって次の行動は違ってきますが、右の図に示すようにマルコフ方策では、状態sまでの履歴にかかわらず、次の行動は状態sで決まってしまいます。(この説明は選ぶ行動は一つですが、より一般的には行動が選ばれる確率です)
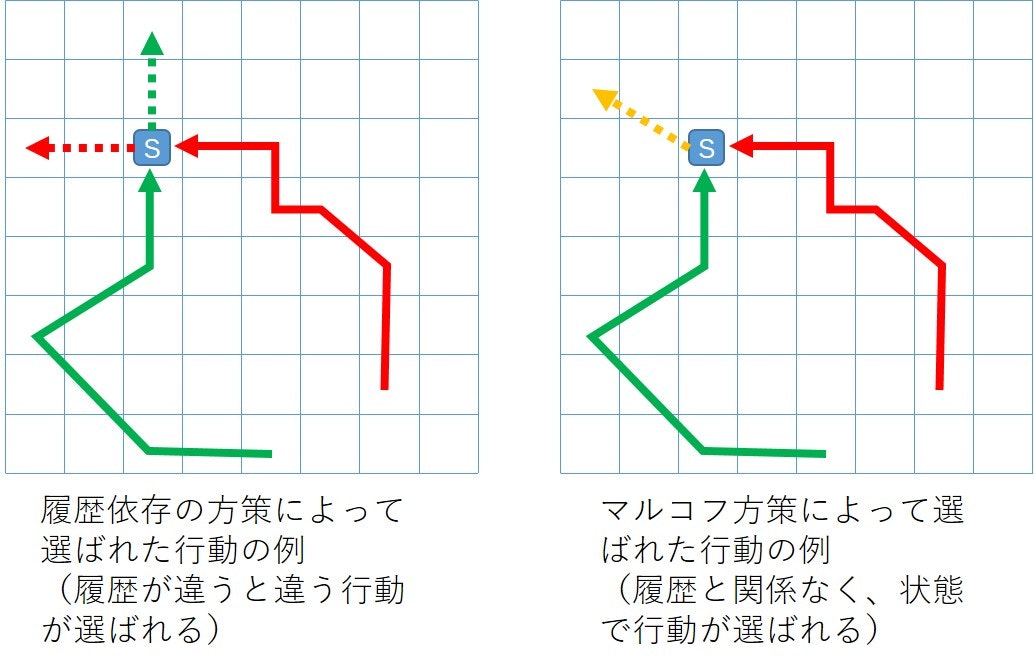
両者の確率が同じとはどういうことでしょうか?
これは、一回の試行を考えているのではなく、履歴依存の方策を複数回試行した場合にそれぞれの状態になる確率とそれぞれの状態での各行動の選択確率が同じになるような、マルコフ方策を作ることができる。イメージはある状態にたどり着く複数の履歴の周辺確率を考える感じです。