はじめに
何の記事?
Fortran Advent Calendar 2023 11日目 で curand を使って乱数を生成したので, その乱数を使って Fortran っぽく数値計算の例を見せようという記事.
Isingスピンとは?
2つの状態を持つ離散的なスピン. スピンが一つの場合は何も面白いことが起きないが, 2次元格子上にスピンを配置して相互作用がある場合は相転移をする.
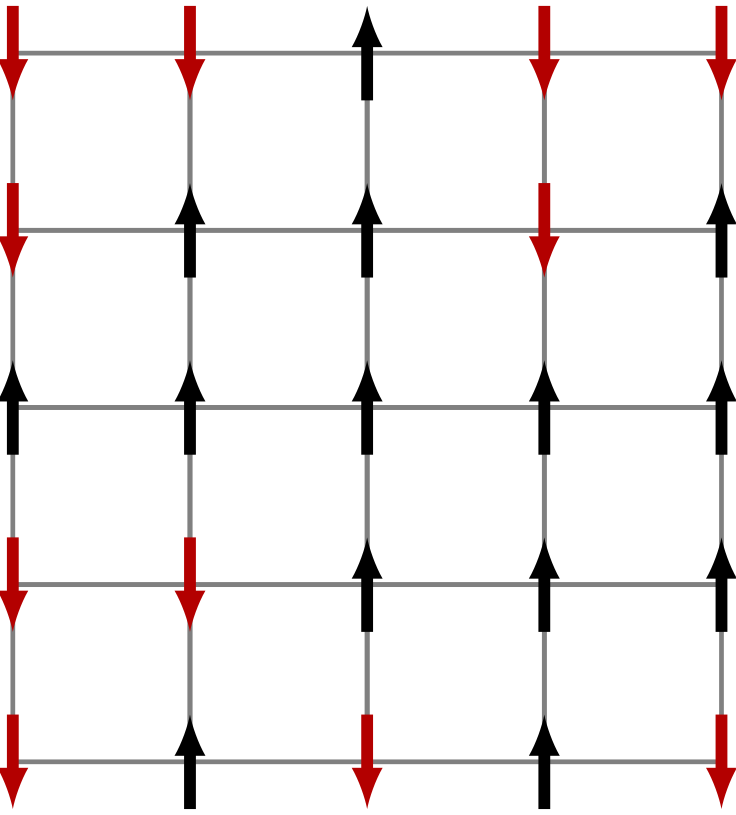
(上の図: 黒と赤の2状態のスピンがあり, 2次元格子状に配置された2次元Ising模型. 相互作用は一番近い4つのスピンとのボンドにある.)
詳しいことは省略. この模型をMonte Carlo シミュレーションでシミュレートする.
確率でスピンを反転させる!(Monte Carlo シミュレーション)
- 2次元Ising模型は全部の状態を生成すれば物理的が分かる.
- が, $2^{(スピン数)}$個の状態があるため, 全部は無理.
- なので, 模型のエネルギーがBoltzmann分布 $\exp(-\beta E)$ の分布に従うようにスピンを反転させる.
($\beta = 1/T$, Boltzmann定数 $k_{B} = 1$ とする.)
- スピン反転のときはエネルギーが $\Delta E$ 変わるので, $\exp(-\beta \Delta E)$ の確率でスピンを反転させると模型がBoltzmann分布に従う.
- 全部の格子に対して順番に $\Delta E$を求めて更新するかしないかを決めるだけ.
- doループとif文だけの簡単なプログラム!
このシミュレーションはGPU計算向き!
- あるスピンを更新することを考えると, そのスピンの更新は最近接の4つのスピンにのみ依存する.
- よって, チェス盤の白マスのスピンを更新→黒マスのスピンを更新, のように交互に更新することで 全体の半分を並列に計算することが可能 である.
GPU計算してみた.
ソースコードはマイGithubに(https://github.com/osada-yum/CUDA_Fortran_MC_simulation_spin).
実行環境
- Ubuntu 20.04.6 LTS
- CUDA 12.2
- NVIDIA GeForce RTX4090
$ cat fpm_run.sh
FCFLAGS="-O2 -acc -cuda -cudalib=curand"
fpm --verbose --compiler='nvfortran' --flag="${FCFLAGS}" run
| サイズ$N$ | Monte Carlo Step $t$ | サンプル数$N_{s}$ | スピンの更新回数$M$ | シミュレーションの掛かった時間 |
|---|---|---|---|---|
| $1001\times1000$ | $1000$ | $100$ | $10^{11}$ くらい | 12秒くらい |
| $1501\times1500$ | $1000$ | $100$ | $2.3\times10^{11}$ くらい | 15秒くらい |
| $2001\times2000$ | $1000$ | $100$ | $4\times10^{11}$ くらい | 20秒くらい |
| $3001\times3000$ | $1000$ | $100$ | $9\times10^{11}$ くらい | 60秒くらい |
| $4001\times4000$ | $1000$ | $100$ | $1.6\times10^{12}$ くらい | 120秒くらい |
| $5001\times5000$ | $1000$ | $100$ | $2.5\times10^{12}$ くらい | 190秒くらい |
| $10001\times10000$ | $1000$ | $100$ | $\times10^{13}$ くらい | 750秒くらい |
- $N = 2001\times2000$ くらいでは計算時間がO$(M)$でないため, GPUが計算を持て余している?
- $N = 5001\times5000$ から $N = 10001\times10000$ では計算時間が$O(M)$のため, GPUをフルに使えている?
結論
- めちゃくちゃ速い.
副産物 (nvfortran でできたこと)
type-bound-procedure が使えた
-
device側(GPU側)で確保する変数も定義することができた.
type :: ising2d_gpu
private
real(real64) :: beta_
integer(int64) :: nx_, ny_, nall_
integer(int64) :: norishiro_begin_, norishiro_end_
integer(int32), allocatable, device :: spins_(:)
real(real64), allocatable, device :: exparr_(:)
real(real64), allocatable, device :: randoms_(:)
type(curandGenerator) :: rand_gen_
contains
procedure, pass :: init => init_ising2d_gpu
! 省略
end type ising2d_gpu
type-bound-procedure から attributes(global) や attributes(device) なやつらを呼び出せる.
シェブロン <<<*, *>>> が付いているやつを呼び出せる.
impure subroutine update_ising2d_gpu(this)
class(ising2d_gpu), intent(inout) :: this
integer(int64) :: lb, ub
lb = lbound(this%spins_, dim = 1, kind = int64)
ub = ubound(this%spins_, dim = 1, kind = int64)
ising2d_gpu_stat = curandGenerate(this%rand_gen_, this%randoms_(1:this%nall_), this%nall_)
call update_sub <<<(this%nall_ + NUM_THREADS - 1) / NUM_THREADS, NUM_THREADS>>> &
& (lb, ub, this%nx_, this%nall_, this%spins_, this%randoms_(1:this%nall_), this%exparr_, 1)
call this%update_norishiro()
call update_sub <<<(this%nall_ + NUM_THREADS - 1) / NUM_THREADS, NUM_THREADS>>> &
& (lb, ub, this%nx_, this%nall_, this%spins_, this%randoms_(1:this%nall_), this%exparr_, 2)
call this%update_norishiro()
end subroutine update_ising2d_gpu
OpenACCプラグマもOK
!$acc parallel loop reduction(+:res) がちゃんと仕事する.
pure integer(int64) function calc_energy_sum_ising2d_gpu(this) result(res)
class(ising2d_gpu), intent(in) :: this
integer(int64) :: i
res = 0_int64
!$acc parallel loop reduction(+:res)
do i = 1, this%nall_
res = res - int(this%spins_(i) * (this%spins_(i + 1) + this%spins_(i + this%nx_)), int64)
end do
end function calc_energy_sum_ising2d_gpu