第5回: アニーリング基礎4. 巡回セールスマン問題

• 東京、島根、大阪、福岡、新潟、香川の6都市を1回づつ巡回する場合、移動距離が最小となる巡回経路をアニーリングを用いて算出する。

前回: 第3回: アニーリング基礎3. クラスタリング問題、2次元スピンの1次元化
参考: 第4回: Google Maps Platform, Directions APIによる地点間情報取得(巡回セールスマン問題への下準備)
Keyword ：巡回セールスマン問題

1. 基本準備/設定

1.1 量子アニーリング用モジュールのインストール

まず、初めに、以下のモジュールをインストールする。

• dwave-ocean-sdk：Dwaveアニーリングマシンのモジュール
• openjij：アニーリングシュミレーター
• pyqubo：Qubo行列作成サポートモジュール
• optuna：ハイパーパラメタの最適化
• geocoder：緯度経度の取得
• folium：地図の表示

pip install dwave-ocean-sdk
pip install openjij
pip install pyqubo
pip install optuna
pip install folium

1.2 Dwaveの初期設定

続いて、Dwaveのtoken、enpoint(アクセスURL)、使用するマシンの指定まで実施。併せて、Jijシュミレーターも設定する。

###基本設定
token = "DEV-73ac79954ef21XXXXXXXXXXXXXXXXXXXXXX"
endpoint = "https://cloud.dwavesys.com/sapi/"
solver = "Advantage2_prototype1.1"
###Dwaveの設定
from dwave.system import DWaveSampler, EmbeddingComposite
dw_sampler = DWaveSampler(solver=solver, token=token, endpoint = endpoint)
###Jijシュミレーターの設定
from openjij import SQASampler
sampler_jij = SQASampler()

2. 定式化

2.1 問題の定義

はじめに、都市間の移動距離、移動時間を、第4回: Google Maps Platform, Directions APIによる地点間情報取得(巡回セールスマン問題への下準備)で整理したGoogle Maps APIから取得する関数を用いて整理する。

###ライブラリのインポート
import geocoder
import requests
import numpy as np

###Google API Keyの設定
google_api_key = "AIzaSyCXLky3OXACXXXXXXXXXXXXXXXXXXXXX"

#===座標取得関数
def _latlng(_location,_object=0):
  _ans = geocoder.osm(_location, timeout=1.0)
  ### geocoderから情報を取得できたか確認
  if _ans.ok == True:
    ### 取得した結果を辞書に変換
    _ans = _ans.json
    if _object == 0:
      ### 後でgoogle mapに代入しやすくするために、検索用のフォーマットに変換する。
      _latlng = str(_ans["lat"]) +"%2C"+str(_ans["lng"])
      ### _object=1の場合、単純に緯度経度をリストで返す。
    elif _object == 1:
      _latlng = [_ans["lat"], _ans["lng"]]
  else:
    _latlng = "error"
    print("Error: ロケーションが見つかりません。")
  return _latlng

#==移動距離と移動時間を取得する関数
def _google_direction(_origin,_destination,_mode="driving"):
  ###APIリクエストの作成
  _mode = "driving"
  _url = f"https://maps.googleapis.com/maps/api/directions/json?destination={_destination}&origin={_origin}&mode={_mode}&key={google_api_key}"

  ###APIデータの取得
  _response = requests.get(_url).json()

  ###移動距離、移動時間の取得
  #Jsonファイルからルート情報の取得
  _route = _response["routes"][0]["legs"][0]
  #移動距離の抽出
  _distance = int(_route["distance"]["value"])/1000
  #移動時間の抽出
  _duration = int(_route["duration"]["value"])/60
  return[_distance,_duration]

def get_dist_time(*target_city):
  ###対象とする都市数の取得
  _N = len(target_city)

  ###出力用の行列を準備
  _distance_inf = np.zeros(_N**2).reshape(_N,_N)
  _duration_inf = np.zeros(_N**2).reshape(_N,_N)

  ### 定義した緯度経度取得するlatlng関数で緯度経度に変換する
  _target_latlng = [_latlng(_tar) for _tar in target_city]
  _target_latlng

  ###組み合わせ事に移動距離、移動時間を取得する
  for _x in range(_N):
    for _y in range(_N):
      if not _x == _y:
        _result = _google_direction(_target_latlng[_x],_target_latlng[_y],"driving")
        #print(f"{_x}:{target_city[_x]}-{_y}:{target_city[_y]}:{_result}")
        _distance_inf[_x][_y] = round(_result[0],0)
        _duration_inf[_x][_y] = round(_result[1],0)
  _result =[_distance_inf,_duration_inf]
  return _result

続いて、今回巡回する都市間の移動距離、移動時間を取得する。

target_city = ["東京都","島根県","大阪府","福岡県","新潟県","香川県"]
_data = get_dist_time(*target_city)
D, T = _data[0],_data[1]#DはDistance, TはTime

実際に得られた結果を、データフレームで整理して表示すると以下の通り。

import pandas as pd
D_df = pd.DataFrame(data = D, columns = target_city, index = target_city)
D_df

出力結果は以下の通り。

次に、スピンを定義する。今回巡回する都市$C$は6都市。当たり前であるが、巡回数$N$は都市の数と同じなので6回。そこで、$x_{nc}$として、$n=3$巡回目で、$c=4$都市に滞在している場合を$x_{34}$として扱うとする。
例えば、下表のような巡回パターンを考える。これは東京→島根→福岡→大阪→新潟→香川の順番で移動していることを意味する。

ス ピ ン $x_{nc}$	東京都 $c=1$	島根県 $c=2$	大阪府 $c=3$	福岡県 $c=4$	新潟県 $c=5$	香川県 $c=6$
1番目 $n=1$	1	0	0	0	0	0
2番目 $n=2$	0	1	0	0	0	0
3番目 $n=3$	0	0	0	1	0	0
4番目 $n=4$	0	0	1	0	0	0
5番目 $n=5$	0	0	0	0	1	0
6番目 $n=6$	0	0	0	0	0	1

2.2 ハミルトニアンの作成

はじめに、エネルギー式を作成する。今回最小化したい対象は移動距離もしくは移動時間である。まずは、移動距離から考える。移動距離の合計値を算出する式をつくる。

E(x)=\sum_{n=1}^N\sum_{c=1}^C\sum_{d=1}^CD_{cd}x_{nc}x_{(n+1)d}

続いて、コスト関数を作成する。2種類ある。まずは1都市に複数回訪問しないというもの。東京都には1回しか行かない。これを定式化すると以下。

C_1(x)=\lambda_1\sum_{c=1}^C(\sum_{n=1}^Nx_{nc}-1)^2

つぎは、一度に同時に複数都市に訪問できないというもの。これを定式化すると以下。

C_2(x)=\lambda_2\sum_{n=1}^N(\sum_{c=1}^Cx_{nc}-1)^2

全てを足し合わせてハミルトニアンの完成。

H_(x)=E(x)+C_1(x)+C_2(x)\\
H_(x)=\sum_{n=1}^N\sum_{c=1}^C\sum_{d=1}^CD_{cd}x_{nc}x_{(n+1)d}+
      \lambda_1\sum_{c=1}^C(\sum_{n=1}^Nx_{nc}-1)^2+
      \lambda_2\sum_{n=1}^N(\sum_{c=1}^Cx_{nc}-1)^2

それでは、実装に移る。

3. 実装

3.1 ハミルトニアンの実装

まずは、スピンとコスト関数の影響度をpyquboを用いて定義する。

### ライブラリのインポート
from pyqubo import Array, Placeholder

### スピンの設定
N, C = len(D),len(D)
x = Array.create(name="x",shape=(N,C), vartype = "BINARY")

### コスト関数の影響度の設定
lambda1, lambda2 = Placeholder("lambda1"), Placeholder("lambda2")

続いて、先ほど整理した以下のハミルトニアンを実装する。

H_(x)=\sum_{n=1}^N\sum_{c=1}^C\sum_{d=1}^CD_{cd}x_{nc}x_{(n+1)d}+
      \lambda_1\sum_{c=1}^C(\sum_{n=1}^Nx_{nc}-1)^2+
      \lambda_2\sum_{n=1}^N(\sum_{c=1}^Cx_{nc}-1)^2

###第1項の実装
E = 0
for n in range(N):
  for c in range(C):
    for d in range(C):
      if n+1 == N:
        E = E + D[c][d]*x[n,c]*x[0,d]
      else:
        E = E + D[c][d]*x[n,c]*x[n+1,d]

###第2項実装
C1 = 0
for c in range(C):
  _c = 0
  for n in range(N):
    _c = _c + x[n,c]
  C1 = C1 + lambda1*(_c -1)**2

###第3項実装
C2 = 0
for n in range(N):
  _c = 0
  for c in range(C):
    _c = _c + x[n,c]
  C2 = C2 + lambda2*(_c - 1)**2

###ハミルトニアンの実装
H = E + C1 + C2

続いて、ハミルトニアンからQubo行列を取り出し、結果を確認してみる。$\lambda_1,\lambda_2$は仮でそれぞれ2000として計算してみる。

###Qubo行列の取り出し
model = H.compile()
Qubo,offset = model.to_qubo(feed_dict={"lambda1":2000,"lambda2":2000})

###Dwaveで計算
sampler_dw = EmbeddingComposite(dw_sampler)
solution = sampler_dw.sample_qubo(Qubo, num_reads=10)
solution.record

rec.array([([1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0], -21298., 1, 0.        ),
           ([1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], -20994., 1, 0.        ),
           ([1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0], -17886., 1, 0.        ),
           ([1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0], -16793., 1, 0.        ),
           ([0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0], -16345., 1, 0.        ),
           ([0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0], -16341., 1, 0.        ),
           ([0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0], -15922., 1, 0.        ),
           ([1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0], -15614., 1, 0.        ),
           ([0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0], -15605., 1, 0.        ),
           ([1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0], -21298., 1, 0.02777778)],
          dtype=[('sample', 'i1', (36,)), ('energy', '<f8'), ('num_occurrences', '<i8'), ('chain_break_fraction', '<f8')])

続いて、結果の可視化関数を定義する。[$C_1(x)$の達成状況、$C_2(x)$の達成状況、移動距離、移動都市]を返す関数とする。

def evaluation(_tar,solution=solution):
  ###C×NのベクトルからC×Nの行列に変換
  _result = []
  for n in range(N):
    _temp = solution.record[_tar][0][n*N:n*N+N]#Dwave結果のtar番目のQubo行列を取得し、C(都市数)行、N(訪問順)列に変換。
    _result.append(list(_temp))
  _result = np.array(_result)

  ###C方向、N方向に合計し、全てに-1した後で、ベクトルを合計し、0でないものを全て1に変換し、更に合計。合計値が0であれば条件達成。
  _result_C, _result_N = np.sum(np.where((np.sum(_result,axis=0)-1)==0,0,1)),np.sum(np.where((np.sum(_result,axis=1)-1)==0,0,1))
  _judge = [1,1]#条件を満たす場合を1とし、以下で条件満たさない場合は0を代入する。
  for _i, _ans in enumerate([_result_C, _result_N]):
    if not _ans == 0:
      _judge[_i] = 0

  ###条件達成した計算結果の経路取得
  if not np.prod(_judge) == 0:#条件を達成している場合に以下を実行(成分の積が1である)
    _answer = []
    for _n in range(N):
      _answer.append(np.where(_result[_n]==1)[0][0])#xncが1の列を取得
    _distance, _route = 0, []
    for _k in range(len(_answer)):
      if _k == len(_answer)-1:
        _distance = _distance + D[_answer[_k],_answer[0]]
      else:
        _distance = _distance + D[_answer[_k],_answer[_k+1]]
      _route.append(target_city[_answer[_k]])
  else:
    _distance, _route = 0, []

  ### Output
  return [_judge[0],_judge[1],_distance,_route]

上で定義した可視化の関数を用いて計算結果を示すと以下。

for i in range(len(solution)):
  print(evaluation(i))

<Output>
[1, 1, 2702.0, ['東京都', '新潟県', '大阪府', '香川県', '福岡県', '島根県']]
[1, 1, 3006.0, ['東京都', '新潟県', '福岡県', '香川県', '島根県', '大阪府']]
[0, 1, 0, []]
[0, 0, 0, []]
[0, 0, 0, []]
[0, 0, 0, []]
[0, 0, 0, []]
[0, 0, 0, []]
[0, 1, 0, []]
[1, 1, 2702.0, ['東京都', '新潟県', '大阪府', '香川県', '福岡県', '島根県']]

続いて、Foliumを使用して、結果を地図上に可視化する。
まず、緯度経度を辞書に代入する。

latlng = {_tar:_latlng(_tar,1) for _tar in target_city}
print(latlng)

<Output>
{'東京都': [35.6828387, 139.7594549], '島根県': [34.9418212, 132.537439], '大阪府': [34.6198813, 135.490357], '福岡県': [33.6251241, 130.6180016], '新潟県': [37.6452283, 138.7669125], '香川県': [34.2480104, 134.0586579]}

次に、マップ上に地点をプロットし、経路をつなぐ直線を追加する関数を定義する。

import folium

def folium_show(_tar=0):
  #初期設定
  _route = evaluation(_tar)[3]

  ### 地図の表示
  _map = folium.Map(
      location = [36,135],
      tiles = "OpenStreetMap",
      zoom_start = 6,
      width = 600, height = 370)
  ### 地点の追加
  for _c in _route:
    folium.Marker([latlng[_c][0],latlng[_c][1]]).add_to(_map)

  ### 経路の追加
  for _k in range(len(_route)):
    if _k == len(_route) -1:
      _origin, _destination = [latlng[_route[_k]][0],latlng[_route[_k]][1]],[latlng[_route[0]][0],latlng[_route[0]][1]]
    else:
      _origin, _destination = [latlng[_route[_k]][0],latlng[_route[_k]][1]],[latlng[_route[_k+1]][0],latlng[_route[_k+1]][1]]
    folium.PolyLine([_origin,_destination]).add_to(_map)

  ### Output
  return _map

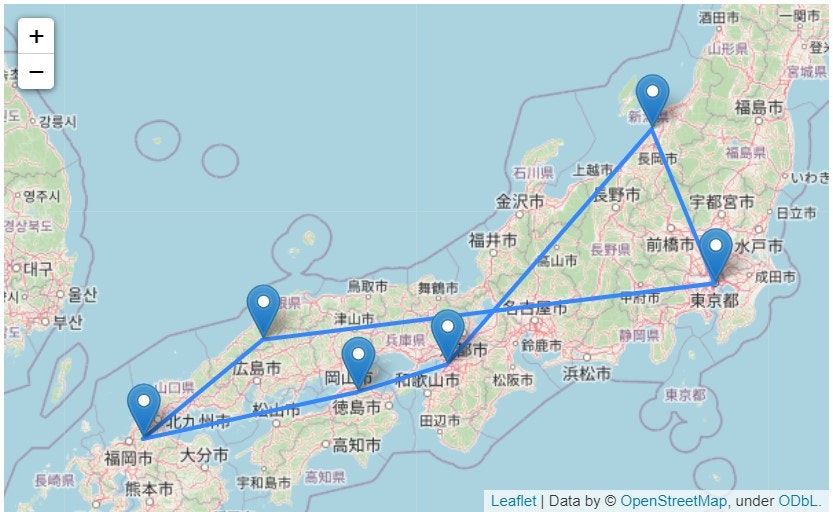
結果は以下の通りとなる。

folium_show(0)

3.2 Optunaによるハイパーパラメタの設定

続いて、Optunaを用いてハイパーパラメタの最適化を実施する。詳細は、第2回: アニーリング基礎2.ナップザック問題、Optunaによるハイパーパラメタ最適化を参照。

###ライブラリの呼び出し
import optuna

###アニーリングを実行する関数の定義
def a_cal(machine = "Dwave", case =100):
### Dwaveかどうかの選択
  if machine == "Dwave":
    sampler_dw = EmbeddingComposite(dw_sampler)
    solution = sampler_dw.sample_qubo(Qubo, num_reads=case)
    
### Jijかどうかの選択
  elif machine =="Jij":
    sampler_jij = SQASampler()
    solution = sampler_jij.sample_qubo(Qubo,num_reads=case)
  return(solution)

###関数の定義
def objective(trial):

  ###ハイパーパラメタの設定
  _lambda1, _lambda2 = trial.suggest_uniform('lambda1', 100, 50000), trial.suggest_uniform('lambda2', 100, 50000)

  ###コンパイルとQuboの取り出し
  model = H.compile()
  Qubo, offset = model.to_qubo(feed_dict={"lambda1":_lambda1,"lambda2":_lambda2})

  ###a_calでアニーリング計算実施し、上で定義したevaluation関数で導かれる移動距離を合計する。ただし、エラーがある場合は移動距離はゼロとする。
  _scoure = 0
  _solution = a_cal("Jij",30)
  for i in range(30):
    _temp = evaluation(i, _solution)
    _scoure = _scoure + _temp[0]*_temp[1]*_temp[2]
    _scoure = -1*_scoure
  return _scoure

### Optunaでの最適化
study = optuna.create_study()
study.optimize(objective, n_trials=50)

### Optunaでの最適解を表示
best_lambda1, best_lambda2= [i for i in study.best_params.values()][0], [i for i in study.best_params.values()][1]
print(f"lambda1: {best_lambda1}, lambda2: {best_lambda2}")

<Output>
[I 2022-11-27 09:21:06,341] Trial 0 finished with value: 2610.0 and parameters: {'lambda1': 43014.053714076465, 'lambda2': 7201.744386238165}. Best is trial 0 with value: 2610.0.
[I 2022-11-27 09:21:06,624] Trial 1 finished with value: 3999.0 and parameters: {'lambda1': 14775.439541998847, 'lambda2': 45176.68249967818}. Best is trial 0 with value: 2610.0.
[I 2022-11-27 09:21:06,910] Trial 2 finished with value: -4748.0 and parameters: {'lambda1': 37667.390645153275, 'lambda2': 19118.30107093418}. Best is trial 2 with value: -4748.0.
...
[I 2022-11-27 09:21:20,410] Trial 49 finished with value: -689.0 and parameters: {'lambda1': 5816.826643356268, 'lambda2': 19034.340848057327}. Best is trial 5 with value: -7832.0.
lambda1: 7804.029841534202, lambda2: 31670.24219567422

得られた最適化なパラメタを用いてハミルトニアンを再度コンパイルし、Dwaveを用いて計算してみる。

model = H.compile()
Qubo, offset = model.to_qubo(feed_dict={"lambda1":best_lambda1,"lambda2":best_lambda2})
solution = a_cal("Dwave")

続いて、計算結果を評価する。

solution.record[:10]

<Output>
rec.array([([0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0], -234134.63222325, 3, 0.),
           ([0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0], -233828.63222325, 1, 0.),
           ([0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0], -233552.63222325, 1, 0.),
           ([0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0], -233412.63222325, 1, 0.),
           ([0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0], -233411.63222325, 1, 0.),
           ([0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0], -232818.63222325, 1, 0.),
           ([0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0], -232801.63222325, 2, 0.),
           ([0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0], -232518.63222325, 1, 0.),
           ([0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], -218600.57254018, 1, 0.),
           ([0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0], -218600.57254018, 1, 0.)],
          dtype=[('sample', 'i1', (36,)), ('energy', '<f8'), ('num_occurrences', '<i8'), ('chain_break_fraction', '<f8')])

結果を可視化してみる。

for _i in range(7):
  print(evaluation(_i))
folium_show(0)

[1, 1, 2702.0, ['東京都', '新潟県', '大阪府', '香川県', '福岡県', '島根県']]
[1, 1, 3006.0, ['東京都', '新潟県', '福岡県', '香川県', '島根県', '大阪府']]
[0, 1, 0, []]
[0, 0, 0, []]
[0, 0, 0, []]
[0, 0, 0, []]
[0, 0, 0, []]

尚、今回Google APIを用いて、移動距離のみならず、移動時間も取得したが、移動時間を最小化する場合は、エネルギー式の$D_{cd}$を$T_{cd}$に変更するだけとなる。

おわりに

今回は、単純な巡回セールスマンモデルを解いてみた。6都市をめぐる場合、何とかアニーリングで結果を得ることができる。一方で、7都市、8都市と増えてくると、計算結果が不安定になってくる。例えば100都市をめぐる場合などは、問題を分割して計算が必要になる。今後検討してみる。また、巡回セールスマンモデルには、時間制限付き巡回セールスマン問題等、複数バリュエーションある。これも今後検討してみる。

今後の課題：巡回セールスマン問題での分割法適用,時間制限付き巡回セールスマン問題
積み残し：補助スピン$y_{i}$の活用, TTSを用いた探索