前書き
DDGK: Leaning Graph Representations for Deep Divergence Graph Kernelsは，グラフデータの分散表現をニューラルネットワークを用いて学習する割と最新めの手法です．(ノードの分散表現ではなく，グラフ全体の分散表現！)2019年発表．graph2vecなどの従来手法は，ノードラベルが必要であったり，事前の特徴量エンジニアリングが必要であったりといった問題点があったのですが，この手法は，それらの問題点を克服しているといえます．
本記事では，この論文の解説を行います．お役に立てれば幸いです．正確さを優先させるのであれば，原著論文を読んだ方が良いと思われるので，本記事は理解を優先した，かなり主観の入った解説になっております．
以下の順で，論文の内容を記述します．
- 研究背景・目的
DDGKが提案される背景となった事実について確認し，DDGKがやりたいことを明確にします． - 手法
DDGKがやりたいことを実現させるために，どのようなことをしているのか確認します． - 実験
手法の有効性を確かめた実験結果を確認します．
研究背景・目的
グラフの分散表現の学習
複雑な構造を持つデータを空間上の１点として埋め込む分散表現の学習は，大変な成功を収めています．良く議論される代表的な手法がword2vec，document2vecなどの自然言語の分散表現学習です．
DDGKは，グラフを空間上の1点(ベクトル)として表現する方法を学習する，グラフの分散表現学習手法の一つです．自然言語や画像データは，系列の順番や空間的な構造といった，ある程度手掛かりになるような構造を持っているのに対して，グラフはそのような制約が存在しない，取り扱いの難しいデータであるといえます．
(注意点)グラフデータをニューラルで扱うといったときに，まず，大きな分岐点となるのが，教師あり学習であるか教師なしの学習であるかといったことだと思います．DDGKは，教師なし学習に分類されるため，分類や回帰といったタスクを処理するためには，DDGKで得られた分散表現を使ってそのようなタスクを処理するモデル(本研究では，SVMを実験で使用)が必要となります．
従来手法の課題
グラフデータを扱う方法は，以前から研究されてきました．大きく3つの分野に分けることができます．
- 教師なし学習
- グラフカーネル
カーネル法をグラフデータに使用します．DeepWalkやWeisfeiler Leman Algorithmが有名なところです． - グラフ統計量
複雑ネットワーク的な分野から派生していた手法で，複雑ネットワークで研究されたネットワークの特徴量エンジニアリングを基に，グラフの表現を求めます．NetSimile法が有名なところです． - グラフラプラシアン
グラフのラプラシアン行列の固有値固有ベクトルをそのグラフの表現に使用するアプローチです．
- グラフカーネル
- 教師あり学習
- GCN
畳み込みニューラルネットワークをグラフの認識に使用する手法です．
- GCN
教師あり学習であるGCNは，本研究の射程外にあります．
教師なしで分散表現を得ようとする従来の手法は，以下のような問題点を抱えています．
- 特徴量エンジニアリングの必要性
例えば，グラフ統計量をとるNetSimile法は，注目すべき7つのノード特徴量(次数，クラスタリング係数等)を挙げ，それらの分布の統計量を取ることによって，グラフ全体の表現を学習しています．これには，人間の仮説(この特徴量が大切だろう)という，主観の入り込む余地が存在します． - Algoritumic heuristics
手法が立脚しているアルゴリズム自体に場合たり的な課題解決が存在している場合があります．例えば，graph2vecは，グラフ内のサブグラフを当てる偽タスクを解決することで，グラフの分散表現を得ていますが，このサブグラフを抽出するために，Weisfeiler Lehman algorithmと呼ばれるサブグラフ抽出手法を用いています．他にも多くの手法が，このWeisfeiler Lehman Algorithmを前提として設計されています．これらの手法は，WL Algorithmに内在する場当たり的な課題解決に依存しているといえます． - ノードラベルの必要性
従来手法の多くが，ノードにラベルが存在していることを仮定しています．
本研究の目的
以上のような背景から，本研究が取り組んでいる問題は，以下のようになります．
ノードラベルの存在しない状況下で，場当たり的な特徴量エンジニアリングやアルゴリズムを使用せず，どのようにして，グラフの分散表現を学習するのか？
この問題に対して，以下の仮説をもって，手法の開発を行っています．
あるグラフ(ターゲットグラフ)の分散表現は，データセット内のグラフ(ソースグラフ)との距離(グラフ構造上どの程度異なるか)によって，定義することができる
手法
問題設定
ノード集合$V$とエッジ集合$E$により，グラフは$G(V, E)$と定義される．グラフデータがM個得られたとする$(G_1, G_2, ..., G_M)$．このとき，グラフ$G_m$の分散表現$\Psi(G_m) \in \mathbb{R}^N$を得ることを目標とする．($N$は分散表現の次元数を表す．)
手法の全体像
- 基本的な考え方
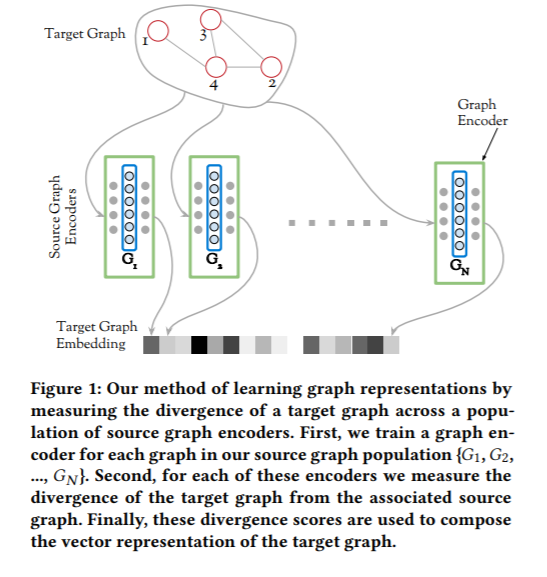DDGKの基本的な考え方は，上述の通り，データセット内のあるグラフの分散表現を同じデータセット内のグラフとの距離によって定義することにあります．ここで，分散表現を得たい方のグラフをターゲットグラフ，ターゲットグラフからの距離を測る方のグラフをソースグラフと呼びます．ターゲットグラフの分散表現の次元数は，ソースグラフに用いたグラフ数になり，$i$番目の要素は，$i$番目のソースグラフとターゲットグラフとの距離になるイメージです．(Figure 1)
- 全体像
では，どのようにして，以上の考え方をニューラルネットワークで実現するのでしょうか？それは，ソースグラフの構造の情報が縮約されたニューラルネットワークの重みを使って，ターゲットグラフの構造を予測するタスクを解くことで実現します．以下の2stepにより，分散表現を学習しています．- ソースグラフの情報縮約(Graph Encoding)
このフェーズでは，次のstepで使用するソースグラフの情報を縮約することを目的とします．$N$個のソースグラフ$G_1, ..., G_N$があるとき，それらの情報が縮約されたニューラルネットワークの重み$\theta_1, ..., \theta_N$を学習します．もちろん，$N$個のニューラルネットワークを構築して，学習することになります． - ソースグラフとターゲットグラフの距離学習(Cross-Graph Attention)
ターゲットグラフの分散表現をソースグラフとの距離によって表現するといいました．ソースグラフ・ターゲットグラフ間の距離をどのように測るかというと，1で作成されたソースグラフの情報が詰まったパラメータを用いて，ターゲットグラフの構造を予測するニューラルネットワークを構築し，そのときの予測誤差を距離としています．
- ソースグラフの情報縮約(Graph Encoding)
以上が全体の流れとなります．以下では，上記の2stepにわけて，DDGKの内容を詳しく見ていきます．
ソースグラフの情報縮約(元論3.1)
- 目標の再確認
N個のソースグラフ$G^S_0, ..., G^S_N$が与えられたとき，ソースグラフそれぞれに対してニューラルネットワークを学習し，その重み$\theta_i(i=0, ..., N)$を獲得する．この重みは，ソースグラフの構造の情報が詰まったパラメータであり，次のステップでそのまま使用する．
- Node-To-Edge Encoder
あるソースグラフ$G^S$に対応するニューラルネットワークの重み$\theta$を学習することを考えます．グラフの構造を学習するやり方は，複数考えられますが，本研究では，Node-To-Edges Encoderと呼ばれる方法を用います．(Figure 2)
- Node-To-Edges Encoderの中身
ソースグラフ$G^S$中のあるノードが与えられたときに，その隣接ノードを予測するマルチラベルの分類タスクとすることで，グラフの構造をニューラルの重み$\theta$に押し込めています．ノードは，ワンホットベクトルとして扱います．自然言語処理における単語がノードとなったようなイメージです．
したがって，最大化の対象となる尤度関数以下の式で表すことができます．$$
J(\theta) = \sum_i \sum_{j, e_{ij} \in E} logPr(v_j| v_i, \theta) $$ここで，$v_i, v_j$は，ソースグラフのノードを意味しています．ソースグラフのあるノード$v_i$が与えられたとき，その隣接($e_{ij} \in E$)ノードが$v_j$である尤度が，$Pr(v_j|v_i, \theta)$です．$Pr(v_j|v_i, \theta)$は，ソースグラフのノード数$V$だけ項のあるカテゴリカル分布であり，そのパラメータは，ニューラルネットワークの出力$f(v_i, \theta)$で与えられます．
最適化の対象となる関数が以上のように与えられるので，誤差逆伝播法を用いて，重みの更新を行うことができます．
ソースとターゲットの距離(元論3.2, 4.1, 4.2)
- 目標の再確認
$M$個のターゲットグラフ$G^T_0, ..., G^T_M$,及び，前章で学習したソースグラフの構造情報を持ったエンコーダー$H_{G^S_1}, ..., H_{G^S_N}$が与えられる(それぞれのパラメータは$\theta_1, ..., \theta_N$)．この時，あるターゲットグラフ$G^T_i$の分散表現$\Psi(G^T_i)$を以下のように表す．$$\Psi(G^T_i) = (D[G^T_i|G^S_1], ..., D[G^T_i|G^S_N])$$ここで，$D[G_i^T|G^S_j]$はグラフ$G_i^T$とグラフ$G^S_j$の距離(疑距離)を表す．
-
基本的な考え方
ターゲット・ソース間の距離を測るために，前章で学習したソースコードのエンコーダーを用いて，Node-To-Edgeと同じタスクをターゲットグラフで解かせることを考えます．ターゲットグラフとソースグラフが構造上近ければ，このタスクを行ったときの予測誤差は小さくなるはずです．逆に，全く似ていない構造をもったグラフ同士であればこのタスクを行ったときの予測誤差は大きくなるでしょう．したがって，この予測誤差をターゲット・ソース間の距離とみなすことができます． -
Cross-Graph Attention(isomorphism Attention)
しかしながら，ターゲットグラフの構造予測(入力をターゲットグラフのあるノード，出力をターゲットグラフの隣接ノードとするタスク)に，前章で学習したエンコーダーをそのまま使用することはできません．なぜなら，両者のノード数やエッジ数が異なり，端的に言えば，入出力時のニューラルネットのノードの数が合わないからです．この課題を解決するために，筆者らは，isomorphism Attentionという，二つのグラフの対応関係を学習するアテンション構造をエンコーダーに取り入れました．(Figure 3)
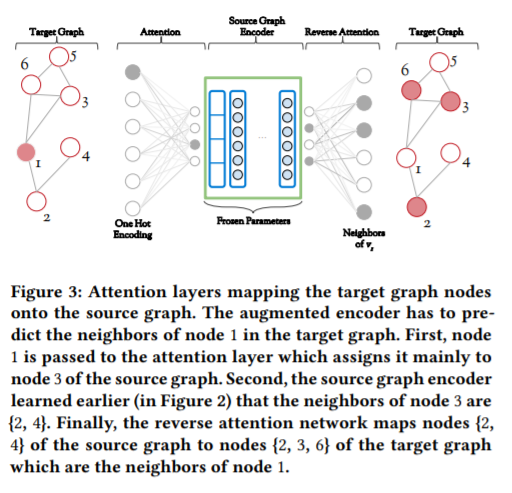このAttention構造は，大きく二つに分かれます．ターゲットグラフのノードからソースグラフへのノードへのアテンション$M_{T→S}$，および，ソースグラフの隣接ノードからターゲットグラフの隣接ノードへのアテンション$M_{S→T}$です.以下，一つずつ説明します．
- ターゲットグラフからソースグラフへ$M_{T→S}$
ターゲットグラフのあるノード$u_i$がソースグラフのどのノード$v_j$と対応しているかを学習します．これには，$u_i$が与えられたとき，ソースグラフのすべてのノードに対する生起確率$Pr(v_j|u_i)$が計算できれば良いです．全結合層$M_{T→S}$とソフトマックス層を用いて，以下のように計算できます．$$Pr(v_j|u_i) = \frac{exp(M_{T→S}(v_j, u_i))}{\sum_{v_k \in V_s} exp(M_{T→S}(v_k, u_i))}$$$M_{T→S}(v_k, u_i)$は，やや特殊な書きかたですが，ノード$u_i$をアテンション$M_{T→S}$への入力としたときの，ノード$v_k$に対応する出力程度の意味でしょう．$V_s$は，ソースグラフのノード集合を意味します．
- ソースグラフエンコーダーの処理
以上の処理によって，ターゲットグラフのノード$u_i$に対応するソースグラフのノード$v_j$が明らかになると，学習済みのソースグラフのエンコーダーを用いて，ソースグラフ上での隣接ノード$N(v_j)$の情報が次の層に渡されます．これは，Node-To-Edgeのところで述べた処理です．
- ソースグラフからターゲットグラフへ$M_{S→T}$
次にソースグラフ上での隣接ノード$N(v_j)$とターゲットグラフの隣接ノード$N(u_i)$との対応関係をアテンション$M_{S→T}$で表現します．$N(v_j)$が与えられたときのある隣接ノード$u_l$の生起確率は，全結合層$M_{S→T}$及びシグモイド関数を用いて以下のように計算できます．$$Pr(u_l|N(v_j)) = \frac{1}{1+exp(-M_{S→T}(u_l, N(v_j)))}$$
-
上記タスクの損失関数
以上の処理をまとめると，結局，エンコーダーのパラメータ$\theta_j$及び，アテンションのパラメータ$M_{S→T},M_{T→S}$を用いて，ターゲットグラフのノード$u_s$が与えられたときの隣接ノード$u_t$を予測していることになるので，損失関数(負の対数尤度関数)は以下のようになります．$$J(M_{S→T},M_{T→S}) = - \sum_s \sum_{t, \ e_{st} \in E_T} logPr(u_t|u_s, \theta_j, M_{S→T}, M_{T→S})$$ -
グラフ間の距離定義，分散表現の獲得
学習後の損失$$J'(M_{S→T},M_{T→S}) = - \sum_i \sum_{l, \ e_{il} \in E_T} logPr(u_l|u_i, \theta_j, M_{S→T}, M_{T→S})$$がそのまま，ターゲットグラフ$G^T_i$とソースグラフ$G^S_j$の距離$D[G^T_i|G^S_j]$になります．これは距離と言ってますが，距離の公理を満たしていない(対称性がない)ので，疑距離です．KLダイバージェンスとかと同じノリです．
この数値をあるターゲットグラフに対して，用意したソースグラフのエンコーダー数分算出すれば，それを並べることで分散表現を獲得することができます．
疑似コードの確認,再び全体像へ(元論4.3)
疑似コードです．記号の使い方がズレているところがあるかと思いますが，適宜読み替えていただきたいです．
2-9行目(Graph Encoding)
N個のソースグラフ$G^S_0, ..., G^S_N$が与えられたとき，ソースグラフそれぞれに対してニューラルネットワークを学習し，その重み$\theta_i(i=0, ..., N)$を獲得する．この重みは，ソースグラフの構造の情報が詰まったパラメータであり，次のステップでそのまま使用する．
10-23行目(ソース・ターゲット間の距離学習→分散表現)
$M$個のターゲットグラフ$G^T_0, ..., G^T_M$,及び，前章で学習したソースグラフの構造情報を持ったエンコーダー$H_{G^S_1}, ..., H_{G^S_N}$が与えられる(それぞれのパラメータは$\theta_1, ..., \theta_N$)．この時，あるターゲットグラフ$G^T_i$の分散表現$\Psi(G^T_i)$を以下のように表す．$$\Psi(G^T_i) = (D[G^T_i|G^S_1], ..., D[G^T_i|G^S_N])$$ここで，$D[G_i^T|G^S_j]$はグラフ$G_i^T$とグラフ$G^S_j$の距離(疑距離)を表す．
その他の事項
以下の事項は，論文中に記載があるものの，省略した部分です．
詳しくは元論をご参照ください．暇があれば追記いたします．
- ノード・エッジラベルが存在する場合
特にこの部分は，一つの節になっていて，重要みが深いと思われます．アテンションの部分に，ノードラベルが一致するような制約条件をかけて，学習する方法が提案されていますが，全体的なフレームワークとしては変わりません． - ソースグラフの数，分散表現の次元数
ソースグラフにもともとのデータセットのグラフをすべて使うと，学習しなければならないニューラルネットの数が膨大となり，計算時間が大変なことになってしまいます．そこで，元のデータセットからサンプリングすることによって計算量を減らすことが提案されています．実験的には，20%程度で十分な性能が出せることが報告されています． - モデルの計算量
- Node-To-Edge以外のGraph Encoding
グラフのエンコーダーに他のタスクを使用することも考えられます．Edge-To-Nodeエンコーディング等．
実験
Attentionの中身を覗く(元論5.1)
- 実験目的
isormorpism attentionがどのようにして，2つのグラフを対応させているのかが知りたい． - 実験方法
ターゲットグラフとソースグラフに2つの同型のグラフ(バーベルグラフ)を用意する．ソースグラフのエンコーダーを学習させた後，isormorphism Attentionにより，2つのグラフの対応関係を学習させ，どのようにノード間が紐づいているかを確認する．(a ラベル無し，b ノードラベル有り，c ノード・エッジラベル有り)を試した． - 結果
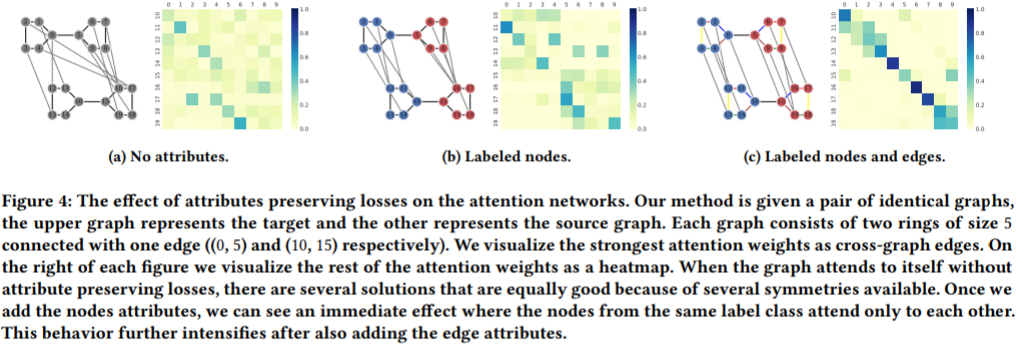
階層的クラスタリング(元論5.2)
- 実験目的
提案手法により，学習された分散表現が，どのような空間を形作るかを知りたい．
→納得感のある埋め込み空間になっているか？近い構造のグラフは，人間が考えても近い位置にあるか？ - 実験方法
大きく分けて2種類のグラフを作る- (1)Mutated Graph
Karate club等の良く知られたグラフデータを基に，それを変形させて新しいグラフ(基になったグラフと似ているが微妙に異なるグラフ)をいくつか作る - (2)Realistic Graph
D&D, PTCといった現実世界のネットワークから同じ種類のネットワークを5つずつサンプルしてくる．
このようにして，合計30のグラフデータを集める．
これらに提案手法を適用し，階層的クラスタリングを行ったものを図示する．
- (1)Mutated Graph
- 結果
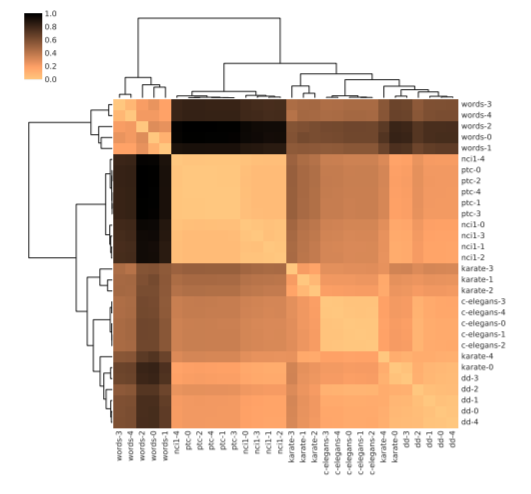
グラフ分類精度による分散表現の評価(元論5.3)
- 実験目的
提案手法により，獲得された分散表現は，他の手法と比較して，より良くグラフの構造をとらえているといえるか？ - 実験方法
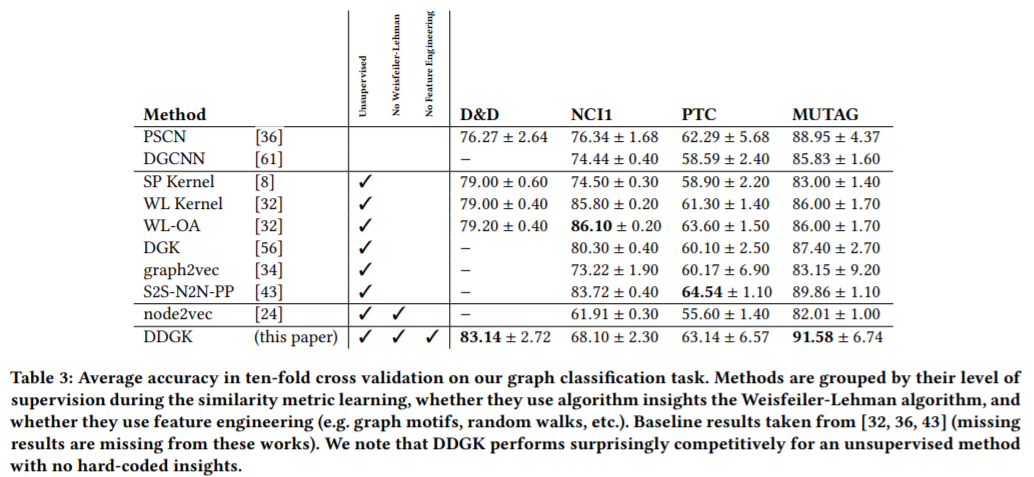
MUTAGなど，あらかじめ，グラフのラベルが付与されているグラフを用いて，その分類精度を比較した．提案手法で獲得した分散表現に対して，SVMを適用し，分類精度を出した．(Cross Validationを用いて，ハイパーパラメータの最適化を行っている．)
教師あり学習手法含めて，複数の手法と分類精度を比較した - 結果
参考文献
あとがき
実験のところの記述テキトーですみません！あとで余裕があったら追記します！