やること
日付で生徒を指名する高校の先生に、その方法はまったくランダムではないことを教えることです。
問題意識
まず、以下のYoutube動画を御覧ください。2:04秒ぐらいです。
https://www.youtube.com/watch?v=k5w35ON0B4I
先生に指名されて問題を解くというのは、高校生からすればできれば避けたいことです。先生もそれを知ってか知らずか、なるべく公平に生徒を指名しようという配慮があります。その配慮・解決策の一つとして、日付を根拠に出席番号を当てられる先生が少なからずおります。ですが、この方法は、まったく公平ではないのではないか、特定の人に最初の指名が集中するのではないかと考えました。そこで、本記事では、シミュレーション実験により、「日付で生徒を指名する先生が陥るバイアス」を明らかにすることを目的とします。
python3.7.4を使用しています。
問題設定及び実験方法
使用したデータは何か? input
どのように実験をしたか? process
結果として何を得たか? output
の順に説明を行います。
input
ここでは入力データの説明をします。
入力として用いるデータは２つ①学年歴②全国苗字人口構成
・学年歴
シミュレーションの舞台となる暦です。2020年度の東京都立の高等学校の暦をできるかぎり忠実に再現しました。具体的には、pythonの標準モジュールcalenderにより2020年と2021年の年間カレンダーを習得し、それらの日付の和集合から休みの日を取り除くことをしています。
・全国苗字人口構成
シミュレーションで、ある高校のあるクラスの一年間の指名状況を観測していくのですが、そのクラスの作成に全国苗字人口構成データを使用しています。具体的には、名字由来ネットさんの名字ランキングデータをスクレイピングして取らせていただきました。https://myoji-yurai.net/
process
ここでは、具体的なシミュレーション方法の概要を紹介します。
- 学年歴と全国苗字人口構成のインプット
- 以下の3.4.の操作を$M$回繰り返す。(今回は$M=10^5$)
- 授業クラスを全国苗字人口構成に基づき生成
- 学年歴に従い、授業を運営し、各人何度先生に指名されたかをカウントする
3.授業クラスを生成
def CreateMember(prob, num):
d = np.random.multinomial(num, prob)
return np.where(d>=1)[0]
上述のコードで、授業を行うクラスを生成することができます。
引数は、probとnumの２つです。
probは、全国苗字人口構成に基づいて算出した、各苗字の発生しやすさを格納したリストです。
ある苗字$i$の発生しやすさを$p_i$,苗字$i$の人口数を$k_i$とすると、$p_i = \frac{k_i}{\sum_j{k_j}}$です。probの$i$番目には$p_i$が格納されてます。
numは、生成する苗字の数です。クラスの人数ではありません。今回は40苗字生成して、もし同じ苗字が複数生成された場合には、重複している数分、クラスの人数が減ることとなります。
CreateMemberでは、各項の発生確率がprobの多項分布からnum数分苗字をサンプリングし、１つ以上サンプリングされた苗字のインデックスを返します。
この授業クラス生成においては、以下の仮定を設けています。
・授業クラスを構成する生徒の名字に地域的な偏りがないこと日本だとある地域に特定の名字が偏ったりしますが、そういったことがないことを想定しています。
・各クラスに同じ苗字を持つ人がいないこと
・CreateMemberにより作成したクラスは、名前の順に出席番号が付けられます
4.各人何度先生に指名されたかをカウントする
以下のコードで、学年歴を一日ずつ追って、その日に指される生徒を決めます。
for oneday in calendar:
attendnum = ChoiceStudent(oneday, csize)
onedayはdatetime.dateオブジェクトです。calenderは、それらを格納したリストで、学年歴を表します。以下、ChoiceStudent関数の実装と説明
def ChoiceStudent(oneday, csize):
m = oneday.month
d = oneday.day
### 実行可能戦略
### 0そのまま1差分2和3積
st = []
if d <= csize:
st.append(0)
if abs(m-d)<=csize:
st.append(1)
if m+d<=csize:
st.append(2)
if m*d<=csize:
st.append(3)
### 戦略実行
if len(st) == 0:
attendum = random.choice(list(range(1, csize+1)))
else:
op = random.choice(st)
if op==0:
attendnum = d
elif op==1:
attendnum = abs(d-m)
elif op==2:
attendnum = d+m
else:
attendnum = d*m
return attendnum
ChoiceStudent関数は、日付とクラスの人数を受け取とり、指名する出席番号を返します。
もっと複雑な、指名の仕方にすることもできるかと思いますが、とりあえず思いついたのは、以下のような先生です。
基本的にとる戦略は4種類1.日付の日と同じ出席番号を当てる2.日付の月と日の差分をとる(7月2日⇒5番)3和をとる(7月2日⇒9番)4.積をとる(7月2日⇒14番)これらの戦略から実行可能なものを選び、複数可能ならばそれらを当確率で選択します。また、いずれも不可能であった場合には、出席番号をランダムに選択します。
上述のコードでは、以下の仮定が設けられています。
・「生徒の指名」は授業のある日に必ず一回だけ行われること
・各戦略はそれが実行可能であるのなら、当確率で起こること。つまり、和をとることを好むなどの嗜好は存在しない。
output
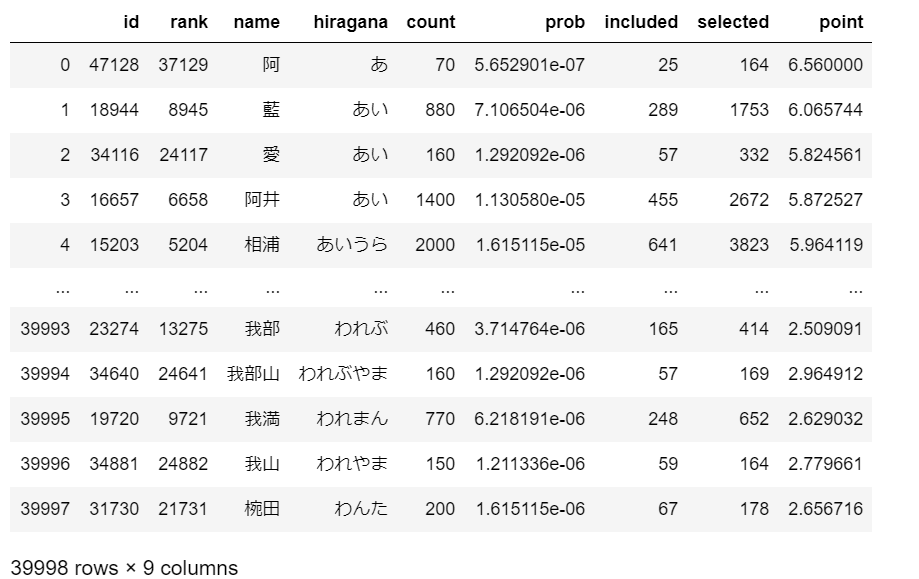上記が最終的にシミュレーションの結果得られるものです。
各カラムの説明をします。
rank:苗字ランキングの順位です。スクレイピングしたときにとりあえずとっておきました。
name:漢字名
hiragana:漢字名をひらがなに変換したもの
count:日本における当該名字の人口
prob:上述の計算方法により算出した、多項分布のパラメタ
included:$M$回のイテレーションのうち、授業クラスに参加した回数
selected:$M$回全てのイテレーションで、先生に指名された回数
point: $point = \frac{selected}{included}$
各苗字の人の指されやすさを素朴に考えれば、selectedを使用するのが適当に思えますが、これでは、クラスに入りやすい人とそうでない人を公平に比較することができません。そこでselectedをincludedで割ったpointという指標を導入しています。
考察
以上のシミュレーションから、各苗字の指されやすさを表すpointをデータとして手に入れることができました。
まずは、シンプルにpointのヒストグラムを観察することで、「日付で生徒を指名する高校の先生が不公平なこと」を明らかにします。
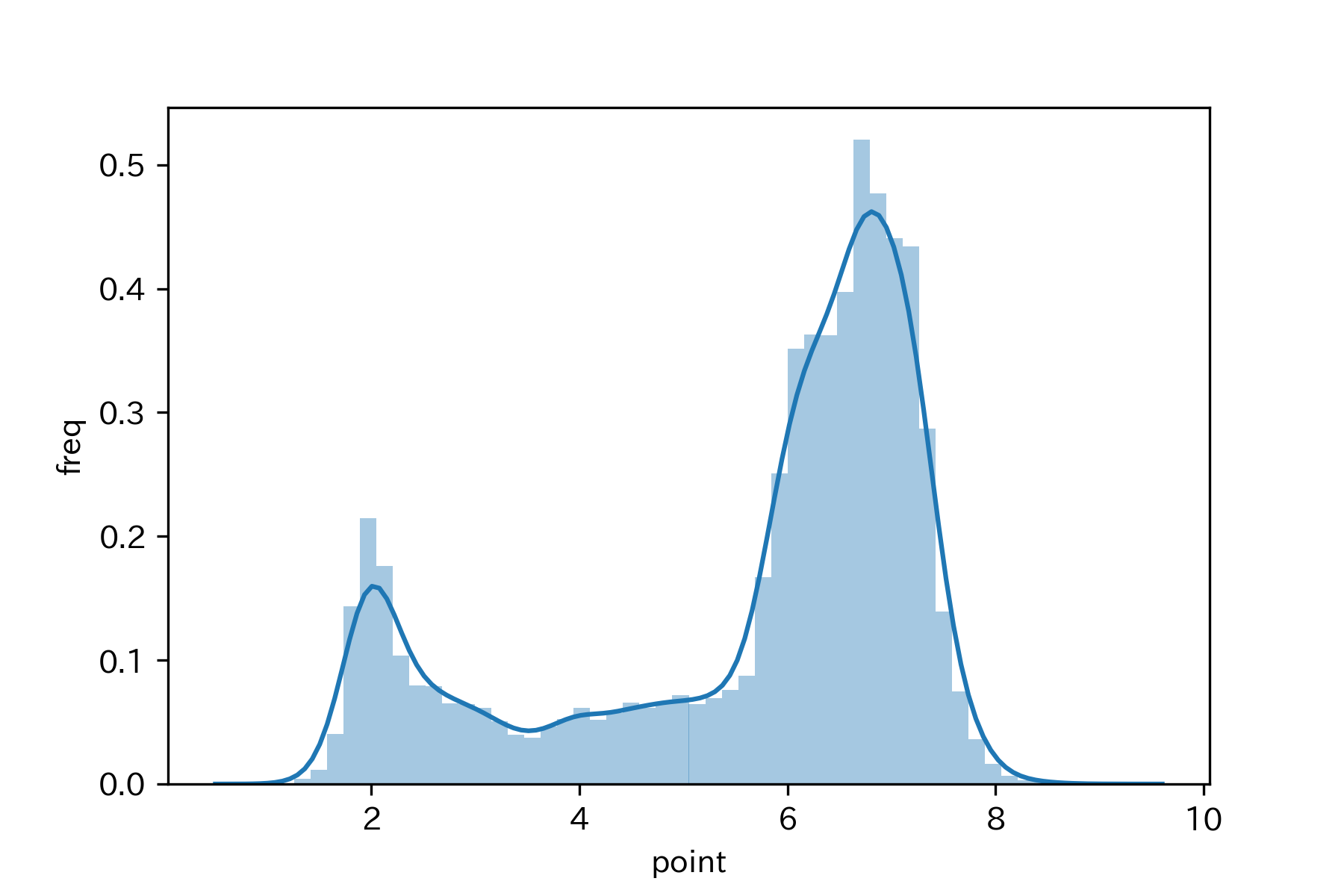
上述のプロットからpointの分布は、2あたりを中心とする正規分布と7あたりを中心とする正規分布が混同した混合正規分布であることがわかります。このことから、低確率で指名される層と高確率で指名される層に苗字が２分割される、すなわち、日付で指名することは不公平な指名のしかたであることがわかります。
それでは、これらの2つの層の苗字は、それぞれどのような性質を持っているのでしょうか？太字で示した仮定のとおり、名前の順で出席番号が与えられていますから、苗字の一番最初の文字に注目するのがよさそうです。
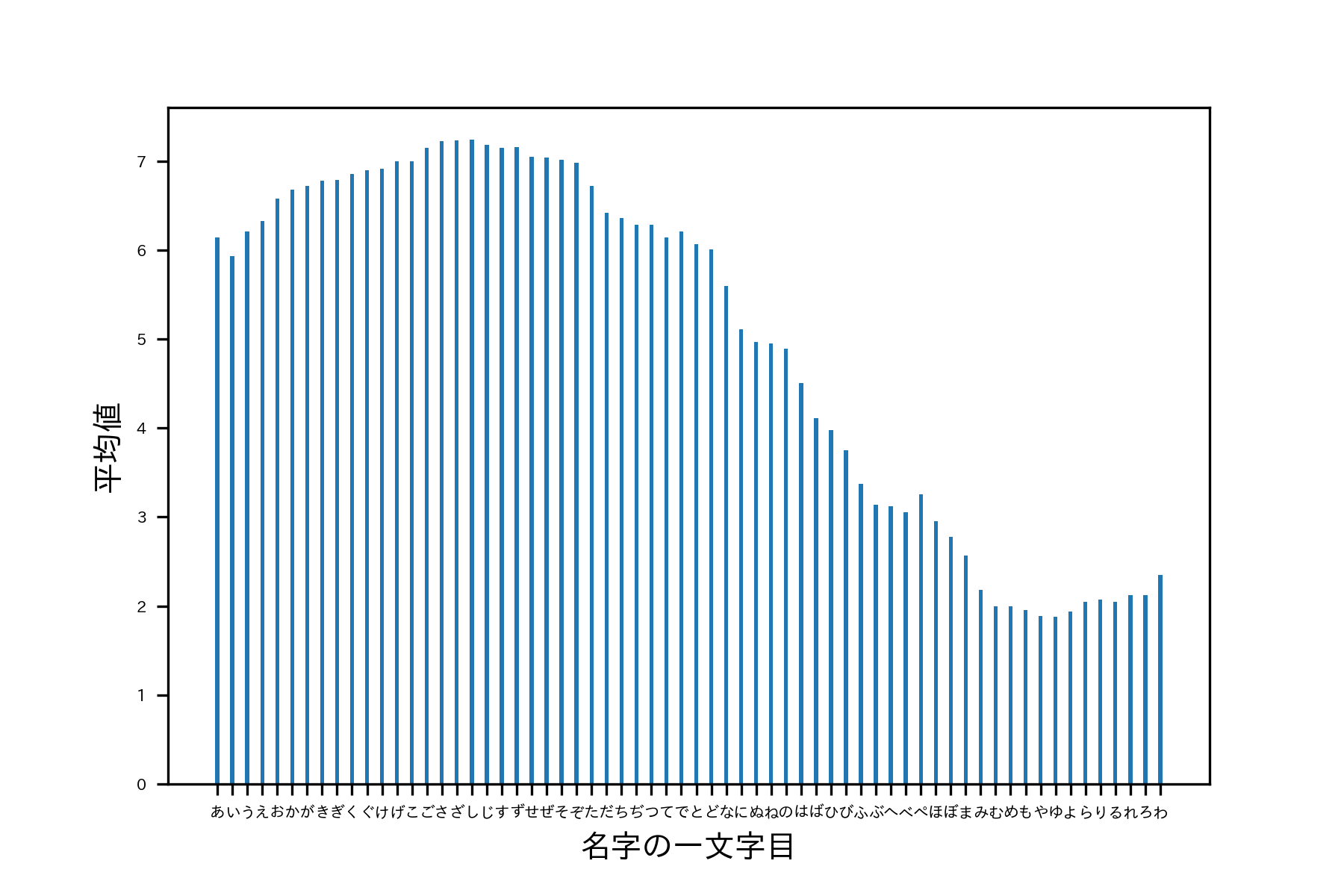
上図は、苗字の一文字目でデータを層別し、それぞれの層のpointの平均値を出したものです。
ここから、ヒストグラムにおける高確率指名層が「かーせ」あたりの名字の人たちであり、低確率指名層が「ほーろ」あたりの名字の人たちであることがわかります。例えば、「し」から始まる生徒は年間で平均して、７回程度指されるのに対して、「や」からはじまる生徒は２回程度しか指されません。
良く指名されるのは、沢田さんや鈴木さんなどさ行か行の方、反対に、あまり指名されないのは、本宮さん山口さんといった出席番号が後ろの方の方でしょう。
結論
「日付で生徒を指名する」というのは、先生からすれば遊びに富んだやりかたなのかもしれませんが、公平性の観点から言えば、不適切であることが明らかになりました。一方で、本記事では「日付で生徒を指名する」やり方について、かなり強い仮定を設けています(4つの戦略しかとれない等)。戦略を工夫することで、ある程度ランダムな日付指名も可能かもしれません。
メモ
シミュレーションコードの共有
高確率層と低確率層が指名されるメカニズムのそれぞれの解明
日付をつかってランダムに指名するには？
それぞれの分析の妥当性強化(比較シミュレーション)
ランキング作成