サイモン・シンの「暗号解読」を読んでいたら、エニグマの仕組みについて説明があり、意外と実装できそうだったので作ってみた。
ソースコードは GitHub にあげています。
※以降、識別がしやすいように平文は小文字、暗号文は大文字で表記している
単一換字式暗号
エニグマは、キーボードで入力された1文字を別の1文字に変換して暗号化する。
このように入力された文字を別の文字に変換する暗号を換字式暗号という。
同じ換字式暗号としては、シーザー暗号が有名。
シーザー暗号では、文字を一定数だけずらすことで暗号化する。
たとえば、3文字ずらすシーザー暗号では、「a -> X」「b -> Y」「c -> Z」「d -> A」のように文字を変換する。
変換表が一種類しか存在しないので、シーザー暗号のような暗号は単一換字式暗号と呼ぶ。
シーザー暗号は単純に文字をずらすだけなので、平文の同じ文字は常に同じ文字で暗号化されることになる(平文中の「a」は、暗号文中では常に「X」になっている)。
この結果、単一換字式暗号には平文と暗号文で文字の出現頻度の傾向が変わらないという特徴が生まれる。
たとえば、英語では「e」の文字が最もよく現れる。
3文字ずらすシーザー暗号では「e」は「B」に変換される。
したがって、暗号文の中で最もよく現れる文字も「B」になる可能性が高い。
僅かな情報だが、このようなヒントに平文の言語の文法や単語の特徴などを加味して分析することで、多くの単一換字式暗号は解読できてしまう。
このように、文字の統計情報をもとに暗号を解読する手法を頻度分析と呼ぶ。
シーザー暗号のような単一換字式暗号は、頻度分析に脆弱となる。
多表換字式暗号
単一換字式暗号の問題点は、暗号化のための変換表が一種類しかない点にある。
その結果、平文の同じ文字は常に同じ文字に暗号化され、平文の統計的な特徴が暗号文に残ってしまう。
そこで、変換表を複数用意する暗号化の方法(多表換字式暗号)が考え出された。
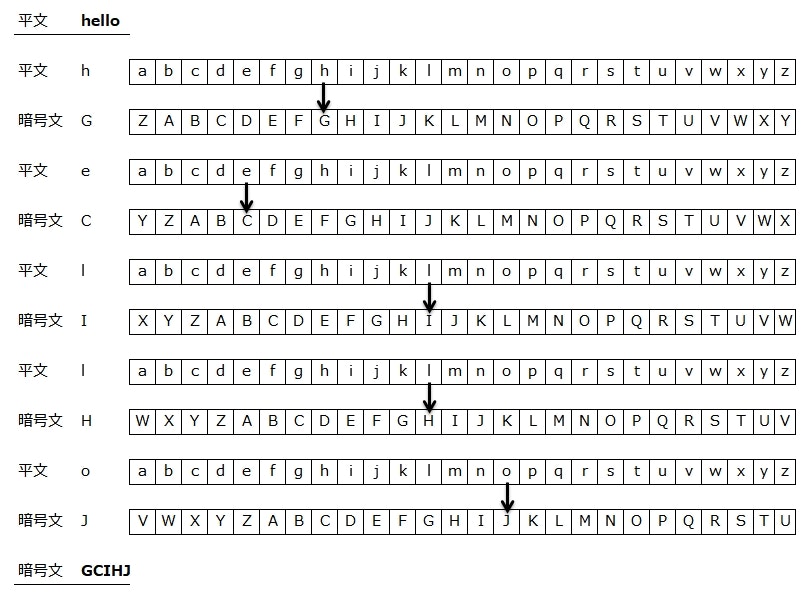
多表換字式暗号では、複数の変換表を用意して、平文の文字ごとに使用する変換表を切り替える。
ここでは、1文字ずつシーザー暗号のシフト量を増やして変換表を切り替えるようにしている。
(※実際はもっと推測しづらい複雑な変換表の切り替え方が必要)
結果として、平文「hello」から「GCIHJ」という暗号文が得られた。
ここで、平文で現れていた「l」という文字は、暗号文上では「I」と「H」という異なる文字に置き換えられている。
このように、文字ごとに変換表を切り替えることで、平文上の同じ文字を異なる文字に暗号化できるようになり、頻度分析による解読を困難にできる。
実際の多表換字式暗号としては、ヴィジュネル暗号という暗号が有名。
ヴィジュネル暗号は、当初は解読不可能と言われていた。
しかし、使用する変換表に周期性があるという弱点を突くことで解読されるようになった。
エニグマ
エニグマは1918年にドイツ人のアルトゥール・シェルビウスによって発明された暗号機で、第二次世界大戦の際にドイツ軍が採用した。
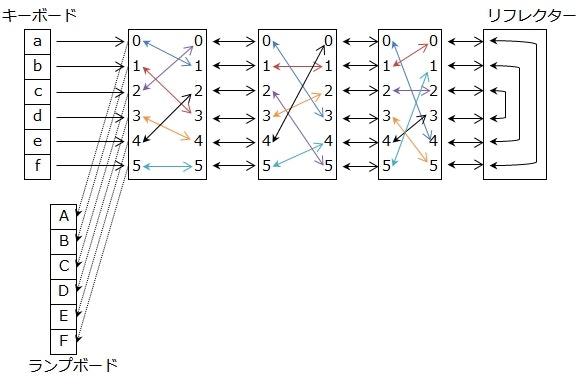
スクランブラー
エニグマは、キーボードで文字を入力すると、ランプボード上の暗号化後の文字が点灯するという形で動作する。
(※画像は「エニグマ」で検索すれば色々出てくるので、そちらを参照)
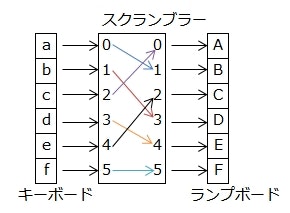
このキーボードとランプボードの間には、スクランブラーと呼ばれる暗号化用の装置が存在する。
スクランブラーは、キーボードで入力された文字をかき混ぜて(スクランブルして)ランプボードに渡す。
これにより、入力された文字は別の文字に変換(暗号化)されることになる。
つまり、このスクランブラーは暗号化のための変換表ということになる。
ローター
単純にスクランブラーを通しただけの暗号化は、単一換字式暗号にしかならない。
単一換字式暗号は簡単に解読されてしまうので、これだけでは強力な暗号装置にはならない。
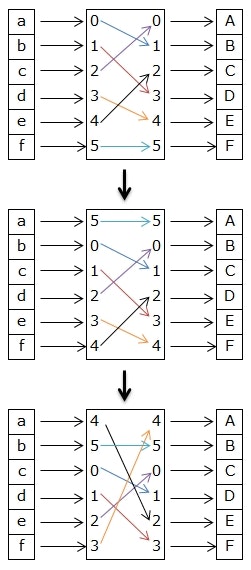
エニグマのスクランブラーは、ローター (Rotor) とも呼ばれ、名前の通り回転することができる。
ローターは、文字が入力されるたびに1文字分ずつ回転するようになっている。
これにより、エニグマは文字を入力するたびに異なる変換表が利用される多表換字式暗号として動作することになる。
上図は簡略化のためa~eの5文字しかないが、実際はアルファベットは26文字ある。
したがって、スクランブラー1つで26種類の変換表を使うことになる。
しかし、これは言い換えると26文字ごとに同じ変換表が利用されるということになる。
この変換表の繰り返しはヴィジュネル暗号の弱点でもあり、同じ変換表が利用されることは極力避けることが望まれる。
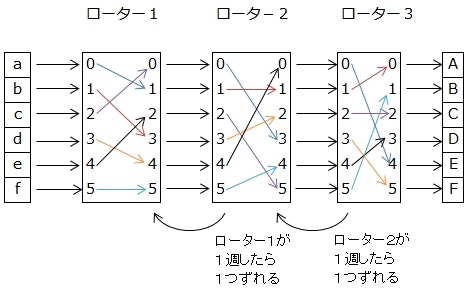
そこで、実際のエニグマでは3つのローターが取り付けられており、2つ目のローターは1つ目のローターが1週したら1つずれ、3つ目のローターは2つ目のローターが1週したら1つずれるという動作をするようになっている。
(※ローターが3つなのは初期のエニグマで、大戦中にローターの数は増やされていった)
この結果、変換表のパターンは $26 \times 26 \times 26 = 17,576$ 通りとなる。
さらに、ローターにセットするスクランブラーは取り替えが可能となっている。
つまり、3つのスクランブラーを3つのローターに自由な組み合わせでセットできる。
そのパターンは6通りなので、変換表のパターンは実質 $17,576 \times 6 = 105,456$ 通りとなる。
リフレクター
前述の模式図では3つ目のローターの次はランプボードになっていたが、実際はリフレクターと呼ばれる特殊なローターが取り付けられている。
リフレクターは、入力された電気信号を反射(reflect)してローター3に返すように動作する。
反射された電気信号はローター2、ローター1と帰っていき、その後でランプボードにつながる。
上図の状態で、例えば「a」をキーボードで入力したとする。
矢印をたどっていくと、最終的にランプボードの「C」にたどり着くことが分かる。
ここで、次はキーボードで「c」を入力した場合を考える。
再び矢印をたどっていく間に気づくかもしれないが、これは先程「a」を入力したときの経路の逆をたどっていることに他ならない。
当然、最終的にはランプボードの「A」にたどり着く。
つまり、ローターの初期状態が暗号化時と一致していれば、暗号文を入力することで平文を得ることができるということになる。
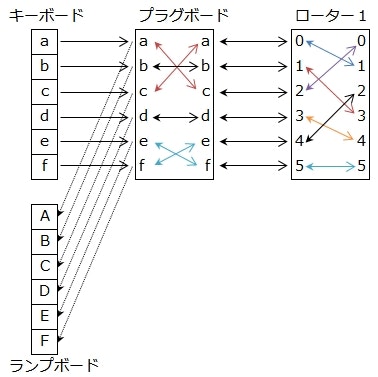
プラグボード
エニグマには、さらにプラグボードと呼ばれる仕組みが用意されている。
プラグボードはキーボードで入力された特定の2つの文字を相互に入れ替える仕組みで、計6つの置き換えを設定できるようになっている。
この例では、「a」と「c」、「e」と「f」の2つの置き換えを設定している。
26文字の中から6つのペアを選ぶパターンは、100,391,791,500 通りにも達する。
ここにローターによる変換表のパターンも掛け合わされることにより、人力での総当たり攻撃は極めて困難となっている。
エニグマの鍵
エニグマの暗号化と復号で必要となる情報は、次の3つになる。
- スクランブラーの配置
- ローターの初期状態
- プラグボードの設定
つまり、これがエニグマの鍵となる。
ドイツ軍は、この鍵を1日1回変更しながら運用していた(大戦の終わり頃は日に何度か変更するようになった)。
日ごとに変更するのでこれを日鍵と呼ぶ。
どの日にどの鍵を使用するかは、コードブックにまとめられ配布されていた。
鍵は毎日交換されるので安心に思える。
しかし、1日にやりとりされるメッセージの量は膨大になる。同じ日鍵で暗号化された暗号文を多く入手できると、それだけ解読できる可能性は高くなる。
このため、実際にはさらにメッセージごとに短い鍵(メッセージ鍵)が使用されていた。
メッセージ鍵はローターの初期状態を決めるもので、「XYZ」のように3文字で表される1。
ローターには文字が刻印されており、文字で回転の位置を調整できるようになっている。
つまり、「XYZ」は1つ目のローターの位置を「X」に、2つ目の位置を「Y」に、3つ目の位置を「Z」にする、という意味になる。
メッセージをやり取りするときは、まず最初にこのメッセージ鍵をランダムに決定する。
そして、メッセージ鍵を日鍵で暗号化して通信相手に送る。
その後は、日鍵のうちローターの初期状態だけをメッセージ鍵で置き換えて暗号文をやり取りする。
こうすることで、日鍵によって作成される暗号文を最小限に抑えるようにしていた。
エニグマを実装する
ここまで説明したエニグマの仕組みを、プログラム(Java)で実装する。
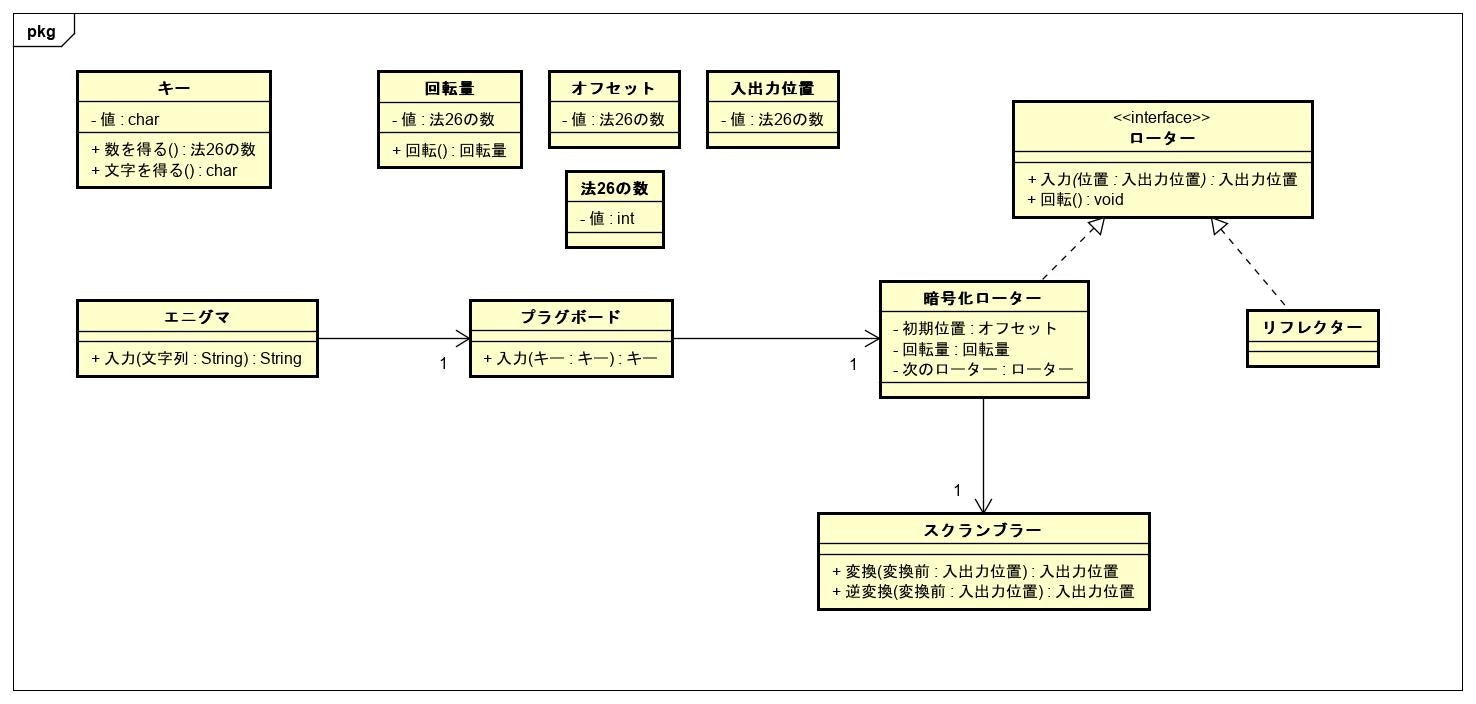
モデル
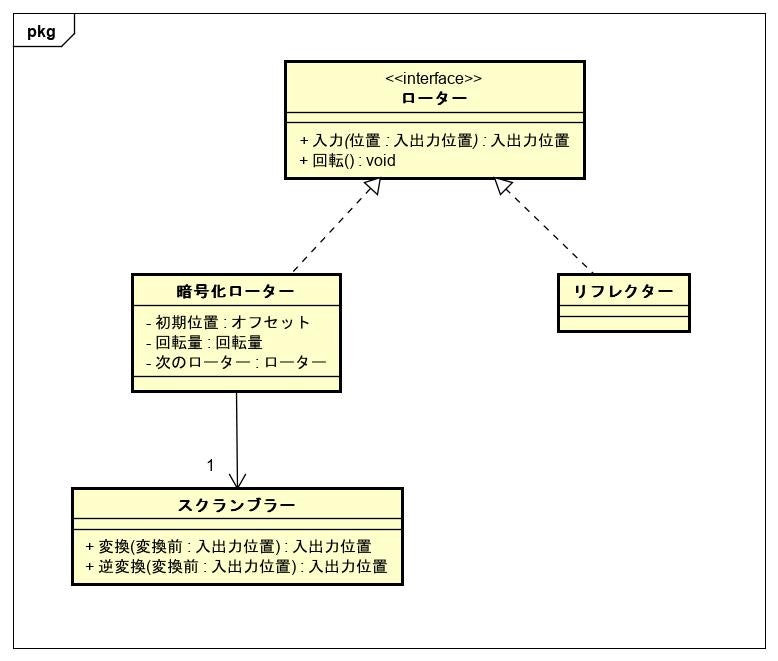
クラス構成は次のようになった。
「エニグマ」クラスが入り口となって、入力された文字列を変換し、結果を文字列で返す。
入力された文字列の情報は、1つ1つ「キー」という単位で分解して、「プラグボード」や「暗号化ローター」に渡されていく。
エニグマのリフレクターが果たす回路の反射は、メソッドの戻り値という形で再現している。
最終的に「プラグボード」が返した「キー」は変換が完了した値で、これを文字列に戻して「エニグマ」の戻り値としている。
クラス図だと「暗号化ローター」が3つあることが表現できていないので分かりづらいが、オブジェクト図にすると次のような感じになる。
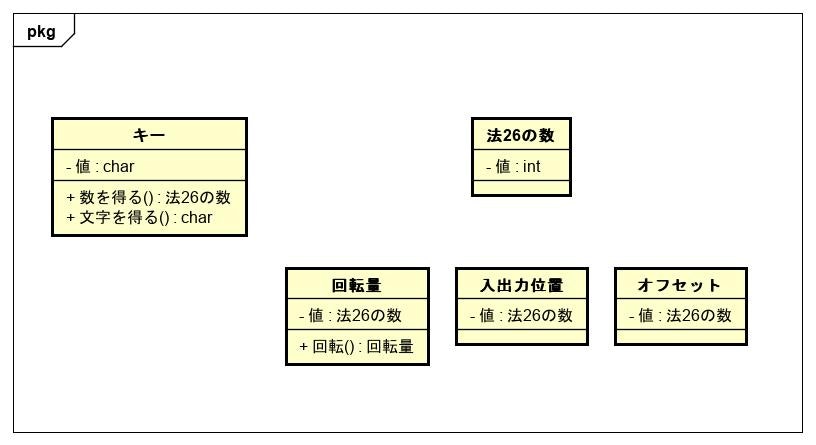
キーと基本型
プログラムで使用する基本的な型として、「キー」「法26の数」「回転量」「入出力位置」「オフセット」がある。
「キー」はエニグマのキーボードで入力されたキー1つ1つを表しており、 a ~ z の 26 文字のいずれかを持つ。
public class Key {
...
static Key of(char c) {
return new Key(c);
}
static Key of(Modulo26 value) {
char key = (char)(value.getValue() + 'a');
return new Key(key);
}
private final char value;
private Key(char value) {
if (!('a' <= value && value <= 'z')) {
throw new IllegalArgumentException("value は a-z のいずれか");
}
this.value = value;
}
char getChar() {
return this.value;
}
Modulo26 toNumber() {
return Modulo26.of(this.value - 'a');
}
...
}
この 26 というアルファベットの文字数を表す数は、ローターの「回転量」や「入出力位置」、「オフセット」などの様々なところで登場する。
さらに、ローターは回転しているので、これらの数はどれも 26 になると再び 0 に戻る特性がある。
これは「26 を法とした数」と言えるので、扱いやすいように「法26の数」というクラスを用意した。
public class Modulo26 implements Serializable {
private final int value;
public static Modulo26 of(int value) {
return new Modulo26(value);
}
private Modulo26(int value) {
this.value = Math.floorMod(value, 26);
}
boolean isZero() {
return this.value == 0;
}
int getValue() {
return this.value;
}
Modulo26 plus(Modulo26 other) {
return this.plus(other.value);
}
Modulo26 minus(Modulo26 other) {
return this.plus(-1 * other.value);
}
Modulo26 plus(int n) {
return new Modulo26(this.value + n);
}
...
}
暗号化ローターとスクランブラー
「ローター」はインターフェースとして定義した。
そして、暗号化で使うローター(「暗号化ローター」)と「リフレクター」を同じ「ローター」として扱えるようにした。
public interface Rotor {
IOPosition input(IOPosition position);
void rotate();
}
public class EncryptionRotor implements Rotor {
private final Offset offset;
private final Scrambler scrambler;
private final Rotor nextRotor;
private RotateAmount rotateAmount;
EncryptionRotor(Offset offset, Scrambler scrambler, Rotor nextRotor) {
this.offset = Objects.requireNonNull(offset);
this.scrambler = Objects.requireNonNull(scrambler);
this.nextRotor = Objects.requireNonNull(nextRotor);
this.rotateAmount = RotateAmount.ZERO;
}
@Override
public IOPosition input(IOPosition position) {
IOPosition scrambled = this.scrambler.scramble(position, this.offset, this.rotateAmount);
IOPosition reflected = this.nextRotor.input(scrambled);
IOPosition reversed = this.scrambler.reverse(reflected, this.offset, this.rotateAmount);
this.rotate();
return reversed;
}
@Override
public void rotate() {
this.rotateAmount = this.rotateAmount.rotate();
if (this.rotateAmount.isZero()) {
this.nextRotor.rotate();
}
}
}
public class Reflector implements Rotor {
@Override
public IOPosition input(IOPosition position) {
return position.plus(13);
}
@Override
public void rotate() {
// Reflector does not rotate.
}
}
こうすることで、「暗号化ローター」が持つ「次のローター」を「ローター」型で抽象化できる。
すると、ローター2が持つ「次のローター(実体はローター3)」とローター3が持つ「次のローター(実体はリフレクター)」を区別する必要がなくなる。
結果、3つのローターをすべて1つの「暗号化ローター」のインスタンスとして作成できるようになる。
エニグマの仕様上「スクランブラー」の配置は自由に変更できる必要がある。
したがって、「ローター」と「スクランブラー」は別のクラスとして抽出した。
「ローター」は回転するものとして初期位置や回転の状態を管理し、「スクランブラー」は変換処理だけを担うようにした。
public class Scrambler implements Serializable {
private final Map<IOPosition, IOPosition> map;
private final Map<IOPosition, IOPosition> reverseMap;
public static Scrambler newInstance(Random random) {
...
}
Scrambler(Map<IOPosition, IOPosition> map) {
...
}
IOPosition scramble(IOPosition input, Offset offset, RotateAmount rotateAmount) {
IOPosition shifted = input.minus(offset, rotateAmount);
IOPosition scrambled = this.map.get(shifted);
return scrambled.plus(offset, rotateAmount);
}
IOPosition reverse(IOPosition input, Offset offset, RotateAmount rotateAmount) {
IOPosition shifted = input.minus(offset, rotateAmount);
IOPosition reversed = this.reverseMap.get(shifted);
return reversed.plus(offset, rotateAmount);
}
public void store(Path path) {
...
}
public static Scrambler load(Path path) {
...
}
}
「スクランブラー」は newInstance(Random) でランダムな配線のインスタンスを生成できるようにしている。
また、このクラスはシリアライズ可能なので、作成したインスタンスは store() メソッドでファイルに出力でき、 load() メソッドで復元することができるようになっている。
プラグボード
public class Plugboard {
private final Rotor rotor;
private final Map<Key, Key> exchangeMap = new HashMap<>();
Plugboard(Rotor rotor) {
this.rotor = Objects.requireNonNull(rotor);
}
public void exchange(Key one, Key other) {
...
this.exchangeMap.put(one, other);
this.exchangeMap.put(other, one);
}
Key input(Key inputKey) {
Key exchanged = this.exchangeMap.getOrDefault(inputKey, inputKey);
IOPosition position = IOPosition.of(exchanged.toNumber());
IOPosition reversed = this.rotor.input(position);
Key reversedKey = Key.of(reversed.getValue());
return this.exchangeMap.getOrDefault(reversedKey, reversedKey);
}
}
「プラグボード」は、 exchange() メソッドでキーの変換ルールをあらかじめ設定しておく。
そして、入力されたキーとローターが返したキーに対して、ルールに従って変換を行っている。
エニグマ
public class Enigma {
private final Plugboard plugboard;
public static Enigma newInstance(
Key firstKey,
Scrambler firstScrambler,
Key secondKey,
Scrambler secondScrambler,
Key thirdKey,
Scrambler thirdScrambler,
Consumer<Plugboard> plugboardInitializer) {
Reflector reflector = new Reflector();
EncryptionRotor thirdRotor = new EncryptionRotor(toOffset(firstKey), firstScrambler, reflector);
EncryptionRotor secondRotor = new EncryptionRotor(toOffset(secondKey), secondScrambler, thirdRotor);
EncryptionRotor firstRotor = new EncryptionRotor(toOffset(thirdKey), thirdScrambler, secondRotor);
Plugboard plugboard = new Plugboard(firstRotor);
plugboardInitializer.accept(plugboard);
return new Enigma(plugboard);
}
private static Offset toOffset(Key key) {
return Offset.of(key.toNumber());
}
private Enigma(Plugboard plugboard) {
this.plugboard = Objects.requireNonNull(plugboard);
}
public String input(String text) {
StringBuilder sb = new StringBuilder();
for (char c : text.toCharArray()) {
Key key = Key.of(c);
Key result = this.plugboard.input(key);
sb.append(result.getChar());
}
return sb.toString();
}
}
「エニグマ」は入出力の受け付けだけでなく、ファクトリとしての役割も持っている。
newInstance() に初期化に必要な情報(エニグマの鍵)を渡すことで、各種インスタンスを生成し、 Enigma インスタンスを返す。
Consumer<Plugboard> plugboardInitializer は「プラグボード」の配線を初期化するための処理を渡すための引数で、次のように実装することをイメージしている。
Enigma encryption = Enigma.newInstance(
Key.D, firstScrambler,
Key.K, secondScrambler,
Key.F, thirdScrambler,
plugboard -> {
plugboard.exchange(Key.A, Key.R);
plugboard.exchange(Key.E, Key.K);
plugboard.exchange(Key.O, Key.T);
plugboard.exchange(Key.P, Key.Q);
plugboard.exchange(Key.Z, Key.M);
plugboard.exchange(Key.Y, Key.C);
});
実際に動かす
import java.security.SecureRandom;
public class Main {
public static void main(String[] args) {
// スクランブラーを生成
SecureRandom random = new SecureRandom();
Scrambler firstScrambler = Scrambler.newInstance(random);
Scrambler secondScrambler = Scrambler.newInstance(random);
Scrambler thirdScrambler = Scrambler.newInstance(random);
// 暗号化用に Enigma インスタンスを生成
Enigma encryption = Enigma.newInstance(Key.D, firstScrambler, Key.K, secondScrambler, Key.F, thirdScrambler, Main::initializePlugboard);
// 暗号化
String encrypted = encryption.input("helloxxworld"); // "xx" は空白スペースを表すための仮の文字列
System.out.println(encrypted);
// 同じキー情報で復号用の Enigma インスタンスを生成
Enigma decryption = Enigma.newInstance(Key.D, firstScrambler, Key.K, secondScrambler, Key.F, thirdScrambler, Main::initializePlugboard);
// 復号
String plainText = decryption.input(encrypted);
System.out.println(plainText.replace("xx", " "));
}
private static void initializePlugboard(Plugboard plugboard) {
plugboard.exchange(Key.A, Key.R);
plugboard.exchange(Key.E, Key.K);
plugboard.exchange(Key.O, Key.T);
plugboard.exchange(Key.P, Key.Q);
plugboard.exchange(Key.Z, Key.M);
plugboard.exchange(Key.Y, Key.C);
}
}
rsonmcqycsjk
hello world
ちゃんと暗号化と復号ができたっぽい。2
おわりに
訳者あとがき
(中略)
いったいシンの才能の秘密はどこにあるのだろうか? (中略)専門家にとってさえ込み入った内容を、ずぶの素人にもわかりやすく、しかも単に上っ面をなでるのではなく、ずっしりと手応えを感じさせるように書けることである。
(中略)
たとえば暗号機エニグマを解説した本はこれまでに何冊も出版されているが、「仮にタイムトラベルで二十世紀初めに戻ったとして、これを読んでおけば自力でエニグマ機を組み立てられるのではないか」、とまで思わされた本は本書だけだった。暗号解読(下)(新潮文庫) 訳者あとがき より
思わされた結果がこれである。
「暗号解読」はエニグマだけでなく中世の暗号から公開鍵暗号まで、幅広く暗号の歴史をカバーしています。
公開鍵暗号は現在のインターネットの通信を支える重要な技術ですが、この本は人類が公開鍵暗号にたどり着くまでの様々な暗号の歴史や、そこに関わった多くの暗号作成者・解読者のドラマを読むことができて非常に面白いです。
例えば、普通に暗号技術について学ぶと「公開鍵暗号は鍵配送問題を解決できる」とさらっとした内容でしか書かれていないことがほとんどですが、鍵配送問題の解決がいかに人類の暗号史において革命的な発明だったのかを、本書を読むと知ることができます。
オススメです。
参考
- 暗号解読 | サイモン・シン | Amazon
- エニグマ (暗号機) - Wikipedia
- 換字式暗号 - Wikipedia
- シーザー暗号 - Wikipedia
- ヴィジュネル暗号 - Wikipedia