#はじめに
点群データを対象とした深層学習モデルで最もベーシックなPointNetを勉強した時の備忘録です。
初めに点群データについて述べ、その後でPointNetの理論の説明とPyTorchによる実装を行う流れです。
またPointNetを使った簡単な実験として、多変量一様分布と多変量正規分布からサンプリングを行い、サンプルがどちらの分布からサンプリングされたものかを当てる二値分類タスクを行っています。
PointNetの論文はこちらです。
実装したコードはGitHubにあります。
#点群データ(Point Cloud)とは
点群データは近年、自動運転の分野で注目されています。というのも自動運転のセンサとして使われているLiDARから得られるデータが点群データであるためです。他には建設業界における三次元計測や分子を対象とした化学計算等で使われており、その応用範囲は多岐に渡ります。(下の猫が点群です。)
点群データですが、3つの重要な性質を有しており、機械学習で点群データを扱う際にはその3つ性質を考慮する必要があります。
###順不変性
順不変性とは点の順列を入れ替えて機械学習モデルに入力したとしても出力が不変であるという性質です。
例えば画像であれば形式が2次元行列で固定されているため、あらゆる画像に対して各要素(ピクセル)に規則的に順番を付けることが可能です。それに対して点群データは画像のように決まった形式を持たず各要素(点)に順番を付けることができないため、機械学習モデルに入力する際には毎回異なった順番で点群が入力されることを想定しなければなりません。この時、異なる順列の点群入力に対して機械学習モデルは毎回同じ値を出力すること(不変であること)が求められます。(そうでないとモデルは入力粒子数の階乗の組み合わせを逐一学習する必要がある。)
つまり次式を満足することが順不変性の条件となります。
$$
f(\boldsymbol x_1, \boldsymbol x_2, ..., \boldsymbol x_M)=
f(\boldsymbol x_{\pi(1)}, \boldsymbol x_{\pi(2)}, ..., \boldsymbol x_{\pi(M)})
$$
ここで$\boldsymbol x_m$は$m$番目の点の三次元座標であり、$\pi$は任意の並べ替え方を表します。
図で表すと以下のようになります.
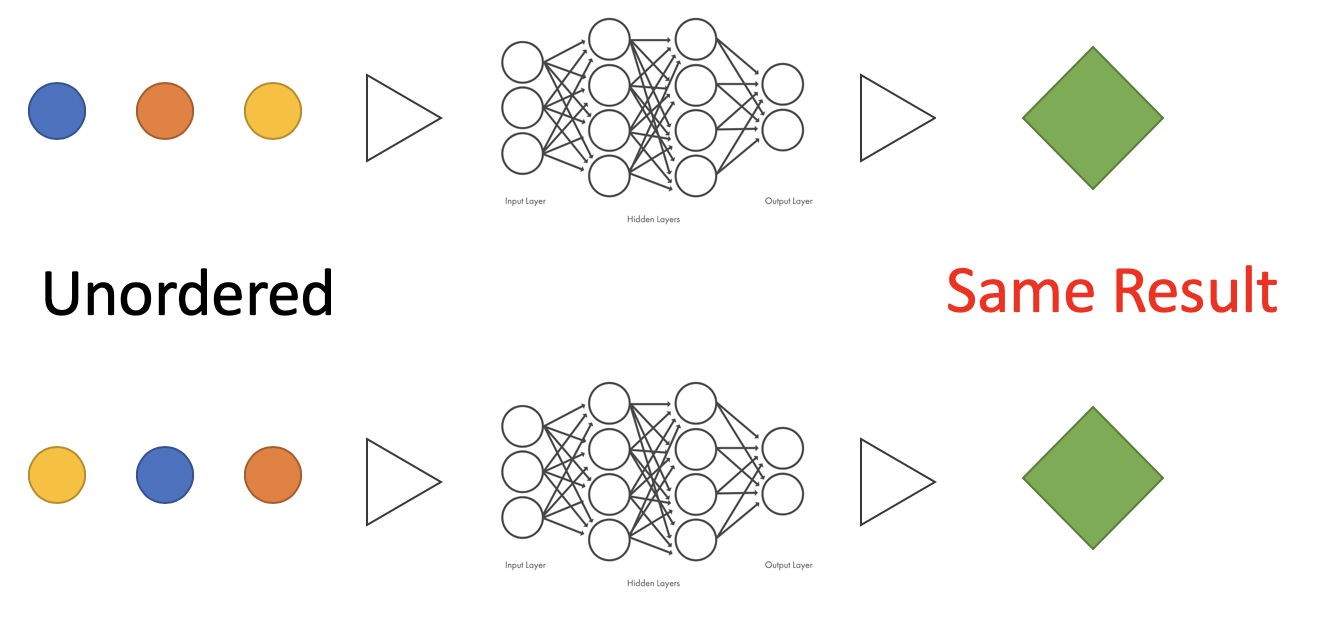
PointNetはMax Poolingという関数を用いることで順不変性を満足しています(後述)。
###移動不変性
移動不変性とは平行移動や回転移動を作用させた点群データを機械学習モデルに入力したとしても出力は不変であるという性質です。
この性質は点群データ固有のものではなく、画像も同じ性質を有しています。(画像はConvolution層を使用することでこの性質を近似的に満足しています)。
平行移動不変性は式で表すと次のようになります。
$$
f(\boldsymbol x_1+\boldsymbol r, \boldsymbol x_2+\boldsymbol r, ..., \boldsymbol x_M+\boldsymbol r)=
f(\boldsymbol x_1, \boldsymbol x_2, ..., \boldsymbol x_M)
$$
入力$\boldsymbol x_m$を任意のベクトル$\boldsymbol r$だけ平行移動させても、出力は変化しないという意味です。
次に回転移動不変性は次式のようになります。
$$
f(R\boldsymbol x_1, R\boldsymbol x_2, ..., R\boldsymbol x_M)=
f(\boldsymbol x_1, \boldsymbol x_2, ..., \boldsymbol x_M)
$$
入力データを任意の回転行列$R$だけ回転移動させても出力は不変であるという意味です。
詳細は後述しますが、PointNetは入力点群に対してアフィン変換(平行・回転移動)を施すことで近似的に移動不変性を獲得しています。厳密に移動不変性を満足しているわけではありません。厳密的に移動不変性を満足するためには、例えば2つの点の距離を特徴量として用いるといった手法が考えられます。
(2つの点を平行移動させたり、回転移動させたりしても、その距離は一定です。なので2点間の距離を特徴量とすることで移動不変性を厳密に満足できます。SchNetやHIP-NNというモデルはそんな感じの手法を使っています。)
###局所性
空間的に近い点同士は何らかの密接な関連性を有していて、空間的に遠い点同士は関連性が小さいという性質が局所性です。この性質も点群特有のものではなく、画像や自然言語も同じ性質を持っているので画像を例に上げると、近くのピクセル同士は似た色になっていたり、またはエッジの周辺では近くのピクセル同士のコントラストが大きくなっていたりと、近接する要素は強い関連性を有していることが分かるかと思います。画像や自然言語ではConvolution層を使用することで局所性を満足することができます。
(実はPointNetは局所性は満足していません。このPointNetの欠点を克服したモデルがPointNet++です。Convolution層に似た機構によって局所性を満足しています。)
#PointNetの理論
下図がPointNetのアーキテクチャです。
青色の部分はClassification Networkであり、黄色の部分はSegmentation Networkです。その名の示す通り、それぞれClassificationとSegmentationという用途で使い分けされます。
今回は青色のClassification Networkの説明だけに留めます。(この部分だけでPointNetの本質は説明可能なためです。)
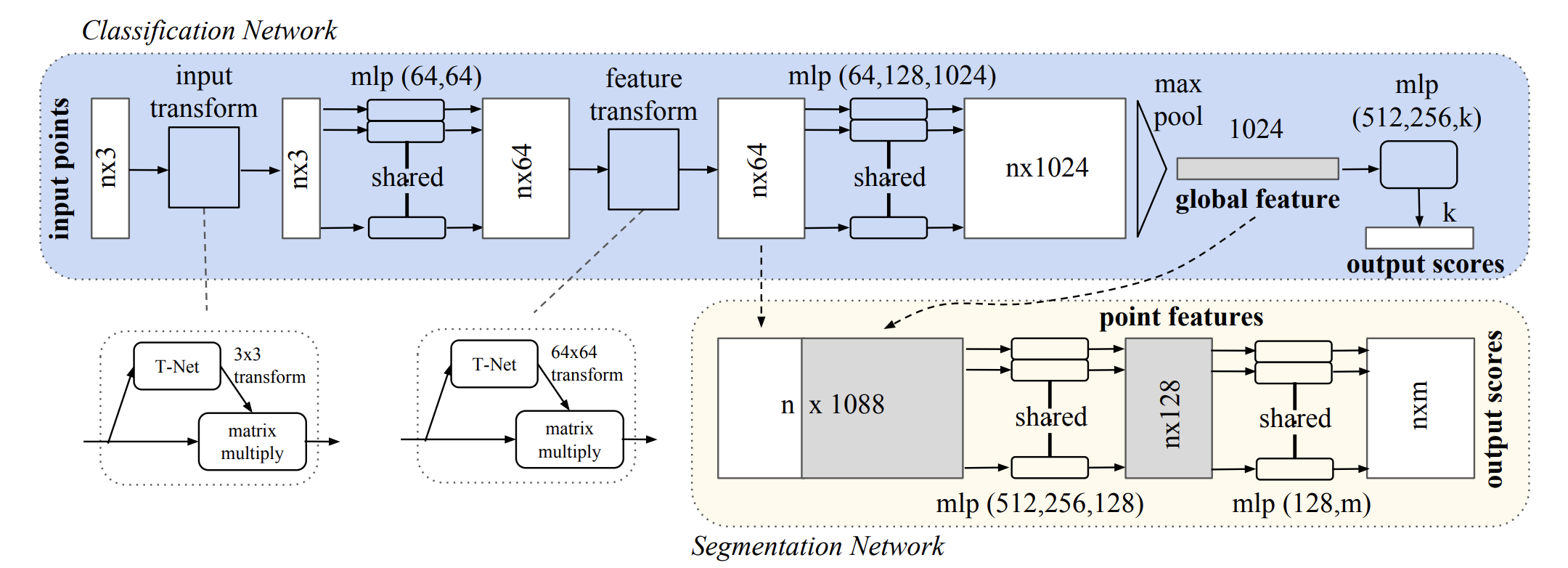
Classification Networkの流れとしては、まずinput transformで入力点群に対してアフィン変換を施し、移動不変性を近似的に獲得します。次にアフィン変換後の点群に対してニューラルネットで処理を行い、feature transformで再びアフィン変換を施します。そしてニューラルネットで処理し、最後にMax Poolingで順不変性を獲得して出力を得ます。
###Max Pooling
PointNetの一番の肝と言われているのががMax Poolingです。Max Poolingは非常にシンプルな関数で、入力要素の内、最大の要素を出力とする関数です。例えば入力要素が{0, 1, 2, 3}だった場合のMax Poolingの出力は最大の要素である3になります。
$$
\rm{MaxPooling}(0, 1, 2, 3)=3
$$
入力要素の順番を入れ替えてMax Poolingに通したとしても出力は変化しないので、Max Poolingは順不変性を満足することが分かるかと思います。
$$
\rm{MaxPooling}(1, 0, 3, 2)=3
$$
PointNetはネットワークの最後の層でMax Poolingを用いることで順不変性を獲得しています。
###Input transform
Input transform (feature transform)はアフィン行列を入力点群に対して作用させることで、入力点群が平行・回転移動され、移動不変性を近似的に獲得します。
アフィン行列ですが、これはT-Netの出力として得ることができます。T-NetはミニPoint-Netのような構造となっていてニューラルネットとMax Poolingの組み合わせからなります。このT-Netに三次元点群を入力してあげると出力としてアフィン行列を得ます。
#実装(PyTorch)
###Input transform(T-Net)の実装
T-Netは三次元点群を入力としてアフィン行列を出力するネットワークです。
以下に示すようにニューラルネット(NonLinear)による非線形変換を繰り返し、途中でMax Poolingを挟んで、最後は(9×1)サイズのTensorを出力します。
この出力を(3×3)にリサイズすることでアフィン行列を得ます。
そして得られたアフィン行列と入力データの行列積を計算して、次のレイヤーに渡します。
なおPointNetの途中の特徴量に対してアフィン変換を行うfeature transformも内容はほとんど変わらないので、説明は省略しています。
class InputTNet(nn.Module):
def __init__(self, num_points):
super(InputTNet, self).__init__()
self.num_points = num_points
self.main = nn.Sequential(
NonLinear(3, 64),
NonLinear(64, 128),
NonLinear(128, 1024),
MaxPool(1024, self.num_points),
NonLinear(1024, 512),
NonLinear(512, 256),
nn.Linear(256, 9)
)
# shape of input_data is (batchsize x num_points, channel)
def forward(self, input_data):
matrix = self.main(input_data).view(-1, 3, 3)
out = torch.matmul(input_data.view(-1, self.num_points, 3), matrix)
out = out.view(-1, 3)
return out
NonLinearはDense, ReLU, Batch Normalizationをまとめた自作の関数です。
class NonLinear(nn.Module):
def __init__(self, input_channels, output_channels):
super(NonLinear, self).__init__()
self.input_channels = input_channels
self.output_channels = output_channels
self.main = nn.Sequential(
nn.Linear(self.input_channels, self.output_channels),
nn.ReLU(inplace=True),
nn.BatchNorm1d(self.output_channels))
def forward(self, input_data):
return self.main(input_data)
###PointNet全体の実装
PointNetは入力→T-Net→NN→T-Net→NN→Max Pool→NN→出力という構成になっています。
これをそのままコードに落とし込みます。
class PointNet(nn.Module):
def __init__(self, num_points, num_labels):
super(PointNet, self).__init__()
self.num_points = num_points
self.num_labels = num_labels
self.main = nn.Sequential(
InputTNet(self.num_points),
NonLinear(3, 64),
NonLinear(64, 64),
FeatureTNet(self.num_points),
NonLinear(64, 64),
NonLinear(64, 128),
NonLinear(128, 1024),
MaxPool(1024, self.num_points),
NonLinear(1024, 512),
nn.Dropout(p = 0.3),
NonLinear(512, 256),
nn.Dropout(p = 0.3),
NonLinear(256, self.num_labels),
)
def forward(self, input_data):
return self.main(input_data)
#実験
簡単な実験として、一様分布と正規分布から三次元データをランダムサンプリングし、PointNetを使ってどちらからサンプリングされたのかを予測する二値分類タスクを行いました。
確率分布からサンプリングを行う関数は以下のような実装になっています。
def data_sampler(batch_size, num_points):
half_batch_size = int(batch_size/2)
normal_sampled = torch.randn(half_batch_size, num_points, 3)
uniform_sampled = torch.rand(half_batch_size, num_points, 3)
normal_labels = torch.ones(half_batch_size)
uniform_labels = torch.zeros(half_batch_size)
input_data = torch.cat((normal_sampled, uniform_sampled), dim=0)
labels = torch.cat((normal_labels, uniform_labels), dim=0)
data_shuffle = torch.randperm(batch_size)
return input_data[data_shuffle].view(-1, 3), labels[data_shuffle].view(-1, 1)
先程実装したPointNetと、このサンプリング関数を使って以下のように学習・評価を行います。バッチサイズは64、1データセット内の点群の数は16です。
new_paramですが、これはTNetの最終層のバイアスの初期値が単位行列(を平坦化したもの)になるように設定しています。論文中でこのような初期化が推奨されています。
batch_size = 64
num_points = 16
num_labels = 1
pointnet = PointNet(num_points, num_labels)
new_param = pointnet.state_dict()
new_param['main.0.main.6.bias'] = torch.eye(3, 3).view(-1)
new_param['main.3.main.6.bias'] = torch.eye(64, 64).view(-1)
pointnet.load_state_dict(new_param)
criterion = nn.BCELoss()
optimizer = optim.Adam(pointnet.parameters(), lr=0.001)
loss_list = []
accuracy_list = []
for iteration in range(100+1):
pointnet.zero_grad()
input_data, labels = data_sampler(batch_size, num_points)
output = pointnet(input_data)
output = nn.Sigmoid()(output)
error = criterion(output, labels)
error.backward()
optimizer.step()
if iteration % 10 == 0:
with torch.no_grad():
output[output > 0.5] = 1
output[output < 0.5] = 0
accuracy = (output==labels).sum().item()/batch_size
loss_list.append(error.item())
accuracy_list.append(accuracy)
print('Iteration : {} Loss : {}'.format(iteration, error.item()))
print('Iteration : {} Accuracy : {}'.format(iteration, accuracy))
結果が次のとおりです。
うまく分類できていることが分かります。(タスクが簡単すぎた説)。
ここで挙げたコードは全体の一部なので、全体を知りたい方はこちらのGitHubをご覧ください。