Python＋Pulpを使ってシフト表を自動作成

はじめに

以前、こういった動画を見ました。
https://www.youtube.com/watch?v=0KRlHHud_dQ/
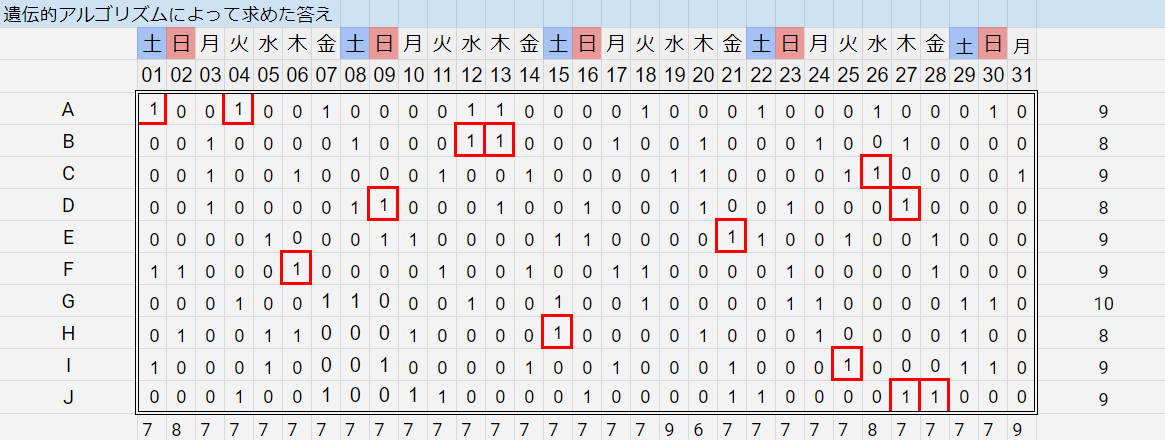
遺伝的アルゴリズムを用いてシフト表を作成するというもの。
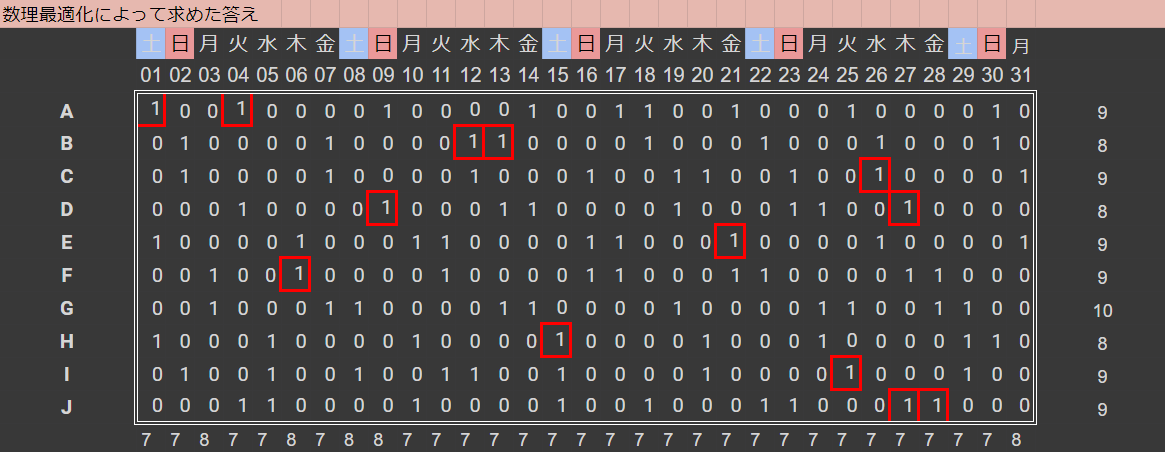
数理最適化というアプローチで同じシフト表を作成してみます。

動画では
Excelから表を取得して再度Excelに吐き出していますが
現状そこは割愛（後々Excel又はスプレッドシートからデータを取得するところから書きます。）

ちなみに環境はGoogle Colaboratoryです。

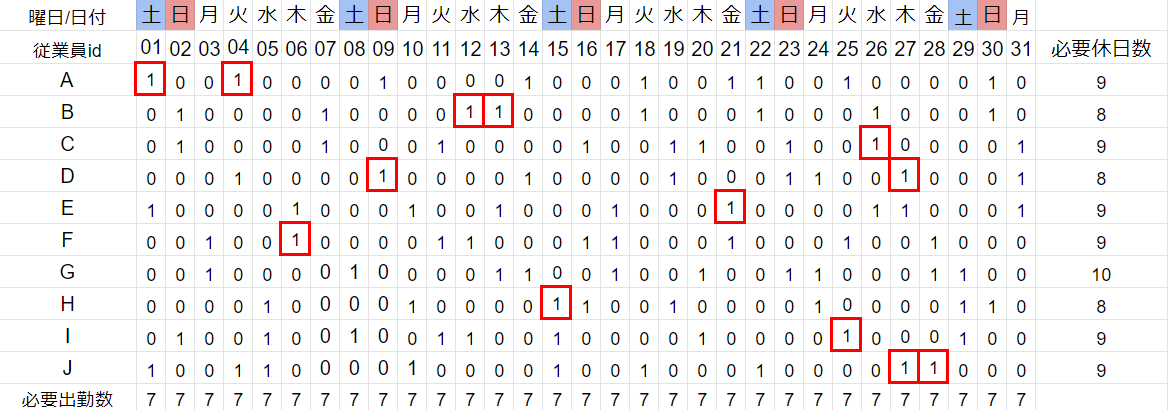
今回作成するシフト表

今回作成するシフト表は
※出勤＝0,休日=1で表現
・1ヶ月が31日
・従業員はA～Jの10名
・各従業員はそれぞれ1カ月中に取得しなければいけない休日数（契約休日数）が設定されている
・各従業員は希望の休日を提出する
・各業務日には必要な出勤数が設定されている（全業務日7名）

このようなシフト表を作成する。

シフト表作成における制約条件

シフト表を作成するルール（制約条件）は
・各従業員に各々の契約休暇日数分の休日を割り当てる
・各営業日における出勤者数を7名～8名で割り当てる
・各従業員の希望休を反映する
・3連休を作らない
・5連勤を作らない
・飛び石連休を作らない（休み⇒出勤⇒休み）

制約条件のイメージ

・各従業員に各々の契約休暇日数分の休日を割り当てる
＞＞各従業員行における「１」の合計が各従業員の契約休日数と等しい

・各営業日における出勤者数を7名～8名で割り当てる
＞＞各営業日列における「０」の合計が7以上8以下

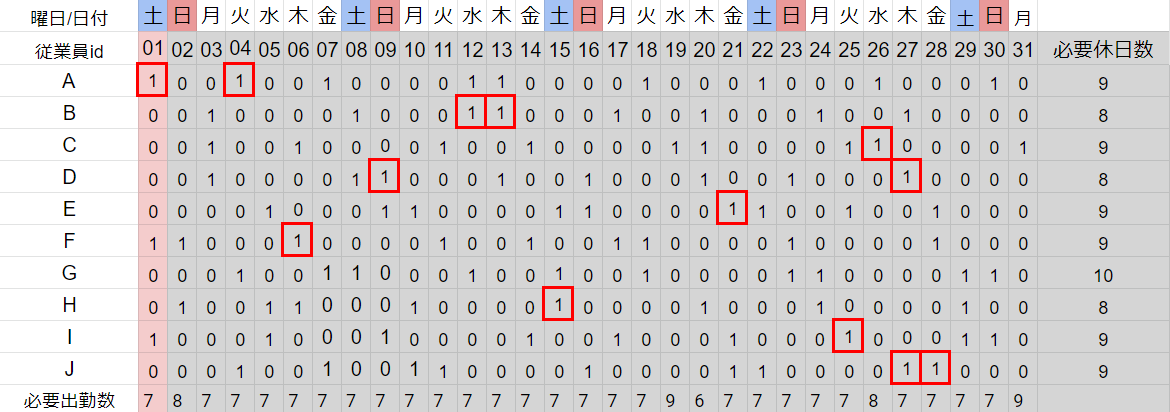
・各従業員の希望休を反映する
＞＞赤枠のマスは必ず「１」を割り当てる

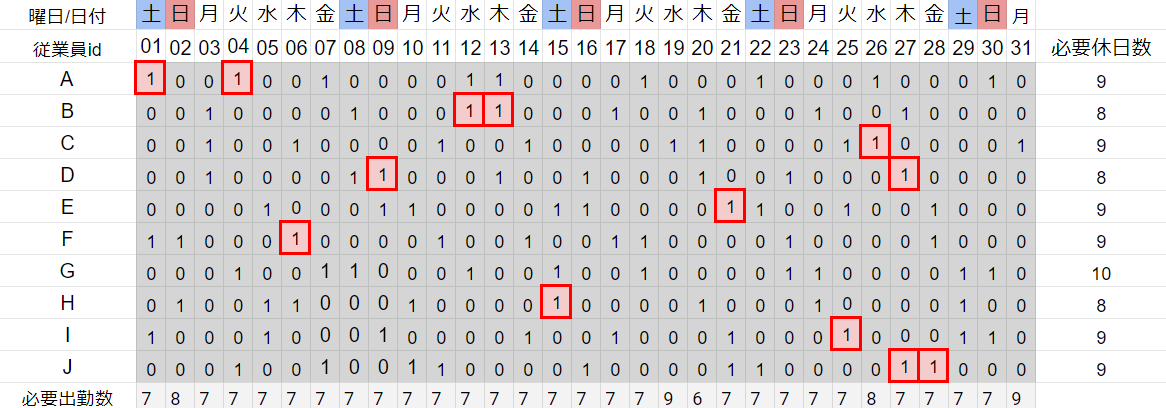
・3連休を作らない
＞＞横方向に隣り合う3マスの数字の合計が2以下
※後述する「飛び石連休を作らない」条件でカバーできるためなくてもOK

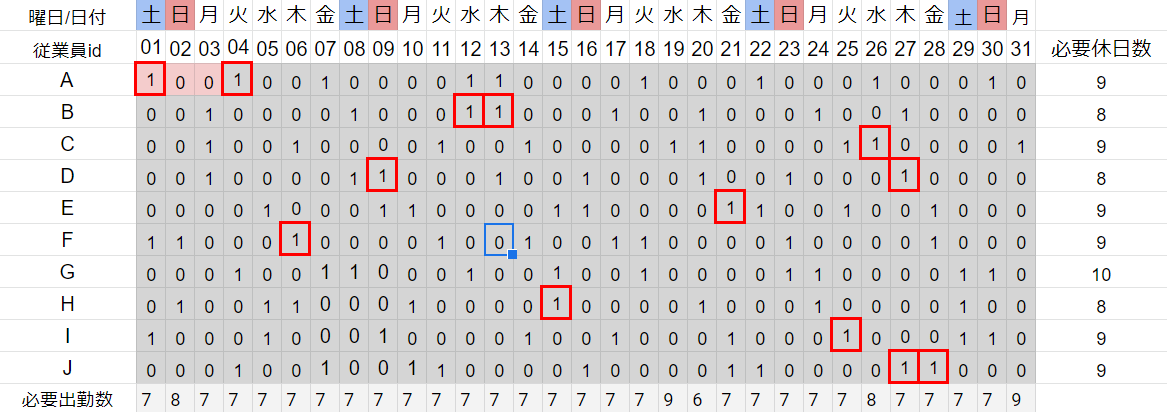
・5連勤を作らない
＞＞横方向に隣り合う5つマス数字の合計が1以上

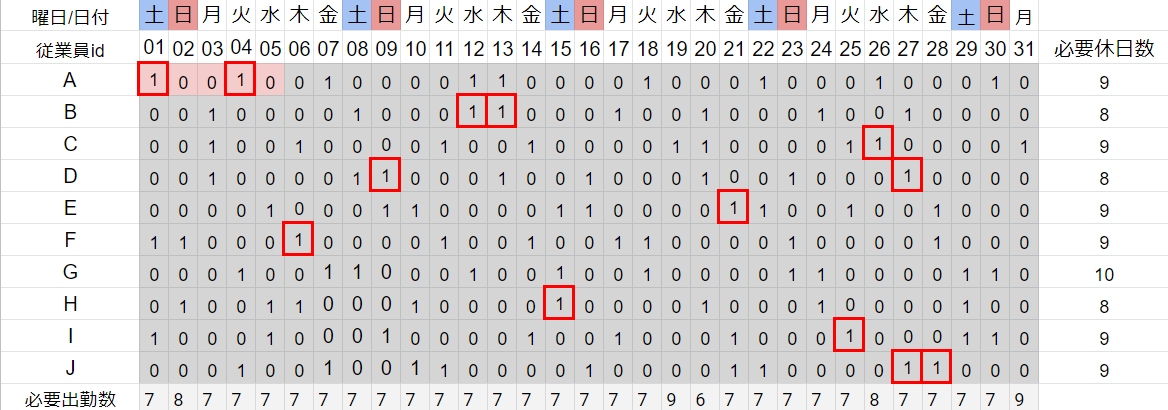
・飛び石連休を作らない（休み⇒出勤⇒休み）
＞＞隣り合う3マスの0，1を「x0、x1、x2」と表現し、「X0 + x2」が1以下
3つの０，１は以下の8パターン
上記の「X0 + x2」を適用すると
「０，０，０」➡ 0
「０，０，１」➡ 1
「０，１，０」➡ 0
「０，１，１」➡ 1
「１，０，０」➡ 1
「１，０，１」➡ 2（飛び石連休）
「１，１，０」➡ 1
「１，１，１」➡ 2（※3連休）

コード全体像

pip install pulp

#ライブラリの用意
import pulp

#リストの定義
#日付リスト
Day = list(range(1,32))

#従業員リスト
Emp = ['a','b','c','d','e','f','g','h','i','j']

#従業員希望休
H_hope = [
          ('a',1),('a',4),('b',12),('b',13),('c',26),('d',9),('d',27),
          ('e',21),('f',6),('h',15),('i',25),('j',27),('j',28)
          ]

#定数の定義
#最適休暇人数リスト
S_req = {d:3 for d in Day}

#必要休暇日数
H_req = {e:hr for e,hr in zip(Emp,[9,8,9,8,9,9,10,8,9,9])}

#最適化モデルの定義
prob = pulp.LpProblem('ShiftFittingProblem',pulp.LpMinimize)

#変数の定義
ED = [(e,d) for e in Emp for d in Day]
x = pulp.LpVariable.dicts('x',ED,cat='Binary')

#制約式の定義
#必要休暇日数を守る
for e in Emp:
  prob += pulp.lpSum([x[e,d] for d in Day]) == H_req[e]

#希望休を守る
for e,d in H_hope:
  prob += x[e,d] == 1

#1日当たりの休暇人数は２～３人
for d in Day:
  prob += pulp.lpSum([x[e,d] for e in Emp]) <= S_req[d]
  prob += pulp.lpSum([x[e,d] for e in Emp]) >= S_req[d]-1

#3連休以上を作らない
for e in Emp:
  for d in Day[:-2]:
    prob += x[e,d] + x[e,d+1] + x[e,d+2] <= 2

#5連勤以上を作らない
for e in Emp:
  for d in Day[:-4]:
    prob += x[e,d] + x[e,d+1] + x[e,d+2] + x[e,d+3] + x[e,d+4] >= 1

#飛び石連休を作らない
for e in Emp:
  for d in Day[:-2]:
    prob += x[e,d] + x[e,d+2] <= 1

#目的関数の定義
'なし'

#求解
status = prob.solve()
print('Status:', pulp.LpStatus[status])

#計算結果の表示
import pandas as pd
display(pd.DataFrame([[x[e,d].value() for d in Day] for e in Emp]))

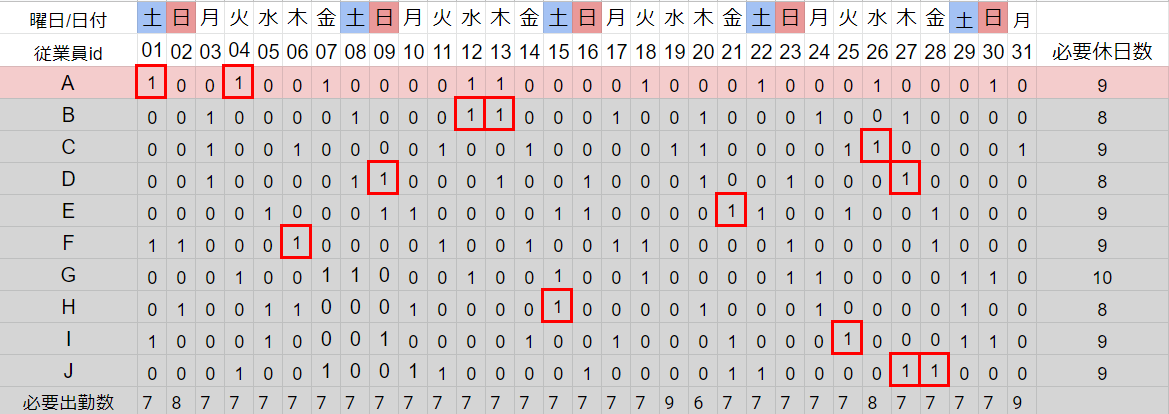
おまけ：遺伝的アルゴリズムとの比較