この記事は
この記事は
「ナース・スケジューリング: 問題把握とモデリング」 を文系初心者にも分かるように図やイラストを追加する_1 の続きとなる記事です。
3章 組み合わせ最適化問題としての定式化
3-3 各ナースの各日程の勤務内容を組み合わせる定式化(p.40)
シフト制約条件
各日各シフトの各グループからの勤務人数の下限と上限を考慮する制約式は、$グループ_r∈R,日_j∈N,シフト_k∈W,下限a_{rjk},上限b_{rjk}$について、
a_{rjk}\leqq\sum_{i∈G_r}x_{ijk}\leqq b_{rjk}と表せる。
1日目においてグループAの日勤の勤務人数に下限が$1$と上限が$2$と設定されていた場合
ナース1、ナース2がグループA、ナース3がグループBとしたとき
赤色の部分の合計が下限($a_{グループA,1,日勤}=1$)以上、上限($b_{グループA,1,日勤}=2$)以下にするという意味です。
この図では赤い部分の合計は$2$なので制約条件を満たしています。
1\leqq x_{1,1,日勤}\;+x_{2,1,日勤}\;\leqq 2
そして、下限を満たせない度合(人数不足)、上限を超過した度合い(過剰人数)を表す非負変数$\alpha^-_{rjk},\alpha^+ _{rjk}$との関係を表すように制約式を変更し、目的関数で$\alpha^-,\alpha^+$の値を最小化させることを考える。変更した制約式は
a_{rjk}-\alpha^-_{rjk}\leqq \sum_{i∈G_r}x_{ijk}\leqq b_{rjk}+\alpha^+_{rjk}となり、目的関数は
Minimize \sum_{r∈R}\sum_{j∈N}\sum_{k∈W}(\alpha^-_{rjk}+\alpha^+_{rjk})とできる。
先ほどと同じ条件で1日目にグループAから1人以上2人以下の日勤者が必要だっと場合に
どうしても調整がつかずグループAからの日勤者が0名の可能性もあります。(下の図)
制約式を破ることはできないため、どう計算しても調整がつかない場合は解なしとなってしまいます。解なしを避けるために、必ず守るハードな制約からできるだけ守るソフトな制約に書き換えているのです。

人数幅(1~2人)の条件をそのままにグループAの1日目、日勤の人数にフォーカスすると
a_{グループA,1,日勤}-\alpha^-_{グループA,1,日勤}\leqq \sum_{i∈G_{グループA}}x_{グループA,1,日勤}\leqq b_{rjk}+\alpha^+_{グループA,1,日勤}\\
1-\alpha^-_{グループA,1,日勤}\leqq x_{1,1,日勤}\;+x_{2,1,日勤} \;\leqq 2 +\alpha^+_{グループA,1,日勤}\\
1-\alpha^-_{グループA,1,日勤}\leqq 0 \;\leqq 2 +\alpha^+_{グループA,1,日勤}
分かりやすく書き直すと
1-不足人数\leqq 0 \leqq 2+過剰人数
この式を満たす上で
\alpha^-_{グループA,1,日勤}+ \alpha^+_{グループA,1,日勤}
目的関数:(不足人数+過剰人数)を最小化したい。つまりできるだけ不足、過剰を避けたい。できるだけ過不足なく人数を集めたいという意味です。$\alpha^-_{rjk},\alpha^+ _{rjk}$は非負変数なので最小値は0です。
\alpha^-_{グループA,1,日勤}=1\\
\alpha^+_{グループA,1,日勤}=0
の時に制約式を満たしたうえで目的関数を最小化できます。
これらの条件をすべてのグループ、すべての日程、すべてのシフトごとに当てはめます。
著者は人数が不足している場合と過剰な場合にて重要度に差を付けたければ
ペナルティとして$w^-_{rjk},w^+ _{rjk}$を設定してあげればよいと記載しています。
ナースが多くて(現場を回すうえで)困ることは少なそうですが
ナースが不足している現場は看護サービスの質を守ることが難しくなるため優先度が高くなりそうです。
目的関数は以下のように表せる。
Minimize \sum_{r∈R}\sum_{j∈N}\sum_{k∈W}(w^-_{rjk}\alpha^-_{rjk}+w^+ _{rjk}\alpha^+_{rjk})
例えば、$w^-_{rjk}=3,w^+ _{rjk}=1$だった場合、不足人数を1人減らすことは過剰人数を3人減らすことと実質的に同じ優先度になります。
ナース制約条件
(1)勤務シフトの回数の下限と上限を守る制約式は、$ナースi∈M,シフトk∈W,下限c_{ik},上限d_{ik}$について、以下のように表せる。
c_{ik}\leqq \sum_{j∈N}x_{ijk}\leqq d_{ik}
赤色部分の合計が下限($c_{ik}$)以下上限($d_{ik}$)以内の範囲に収まるための制約条件です。
図では赤色部分はナース3の日勤の範囲を指しています。
例えば$c_{3,日勤}=1,d_{3,日勤}=3$であればナース3の日勤の合計は$2$なので制約条件を満たしています。

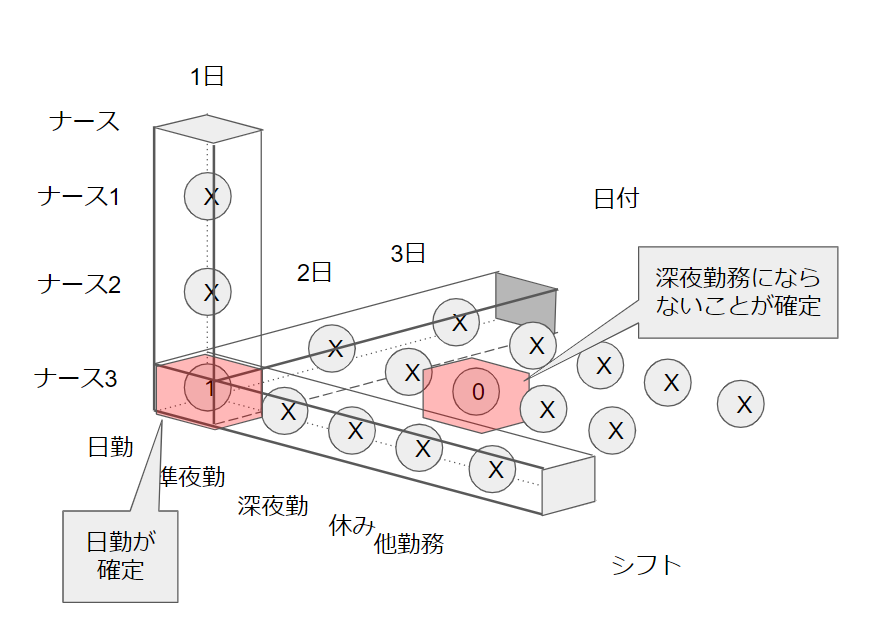
(2)セミナー等の確定勤務や休み希望を達成するために、確定している$ナースi$の$日j$の$シフトk,(i,j,k)\in F_1$は、
x_{ijk}=1逆に、不可能な$ナースi$の$日j$の$シフトk,(i,j,k)\in F_0$は、
x_{ijk}=0と固定する。
(3)禁止されているシフトの並びを避けるために、下に示すa),b),c)を考える。
<中略>
a)同一シフトの連続日数
$ナースi\in M$の$シフトk\in W$の連続日数の下限$e_k$を守るために、$日j\in N$までのe_k+1日分の変数を使って、以下の制約式を考える。\sum_{h=2}^{e_k}x_{i,j-h,k}-(e_k-1)x_{i,j-1,k}+(e_k-1)x_{ijk}\geqq0
連続して同じシフト(ナース3の場合)というのは下の図、赤い部分の$x_{ijk}$の0-1の並びを確認すればわかります。
例として3連続を考えます。
3連続以上か否かについて考える場合は4日間の並びを確認すればよいです。
OK…3連続以上またはその可能性が残っている並び
NG…3連続未満の並び
0,1の4つの並びなので全部で16パターンです。
| 1日目 | 2日目 | 3日目 | 4日目 | 判定 | |
|---|---|---|---|---|---|
| パターン1 | 0 | 0 | 0 | 0 | OK |
| パターン2 | 0 | 0 | 0 | 1 | OK |
| パターン3 | 0 | 0 | 1 | 0 | NG |
| パターン4 | 0 | 0 | 1 | 1 | OK |
| パターン5 | 0 | 1 | 0 | 0 | NG |
| パターン6 | 0 | 1 | 0 | 1 | NG |
| パターン7 | 0 | 1 | 1 | 0 | NG |
| パターン8 | 0 | 1 | 1 | 1 | OK |
| パターン9 | 1 | 0 | 0 | 0 | NG |
| パターン10 | 1 | 0 | 0 | 1 | NG |
| パターン11 | 1 | 0 | 1 | 0 | NG |
| パターン12 | 1 | 0 | 1 | 1 | NG |
| パターン13 | 1 | 1 | 0 | 0 | NG |
| パターン14 | 1 | 1 | 0 | 1 | NG |
| パターン15 | 1 | 1 | 1 | 0 | OK |
| パターン16 | 1 | 1 | 1 | 1 | OK |
先ほどの制約式の左辺は
\sum_{h=2}^{e_k}x_{i,j-h,k}-(e_k-1)x_{i,j-1,k}+(e_k-1)x_{ijk}
上記全パターンの内
OK並びパターンであれば0以上となり
NG並びパターンの時に0未満の値を返します。
例えば下限$e_k=3,日j=4$の時
\begin{align}
\sum_{h=2}^{e_k}x_{i,j-h,k}-(e_k-1)x_{i,j-1,k}+(e_k-1)x_{ijk}\geqq0\\
x_{i,4-2,k}+x_{i,4-3,k}-(3-1)x_{i,4-1,k}+(3-1)x_{i4k}\geqq0\\
x_{i1k}+x_{i2k}-2x_{i3k}+2x_{i4k}\geqq0\\
\end{align}
分かりやすくすると
(3日前)+(2日前)-2*(1日前)-2*(基準日)\geqq0
上述の16パターンを代入すると0以上か否かでによって3連続(以上の可能性含む)を抽出できていることが分かります。また、$日j$の値によって判定される場所が変わります。

次に、$ナースi\in M$のシフト$k\in W$の連続日数の上限$f_k$を守るために、$日j\in N$までの$f_k+1$日分の変数を使って、以下の制約式を考える。
\sum_{h=0}^{f_k}x_{i,j-h,k}\leqq f_k
これは非常にシンプルです。
例えば上限$f_k=4$だった場合
x_{i,j-0,k}+x_{i,j-1,k}+x_{i,j-2,k}+x_{i,j-3,k}+x_{i,j-4,k}\leqq 4\\
分かりやすくすると
基準日+1日前+2日前+3日前+4日前\leqq 4\\
つまり過去5日間の意思決定変数$x_{ijk}$の合計が4以下であればよいということです。
5連続というのは過去5日間がすべてが1であった場合のみだからです。

続き