この記事の目的
暗号技術の概要について説明する。
本記事で扱う暗号化技術
- 秘密鍵暗号技術
- 公開鍵暗号
- 一方向ハッシュ関数
- メッセージ認証コード
- デジタル署名
- 認証局
本記事で説明すること
暗号化技術について、以下のことを説明する。
- 概要
- 暗号化フロー
- アルゴリズム
- 課題
- 対応策
秘密鍵暗号技術
概要
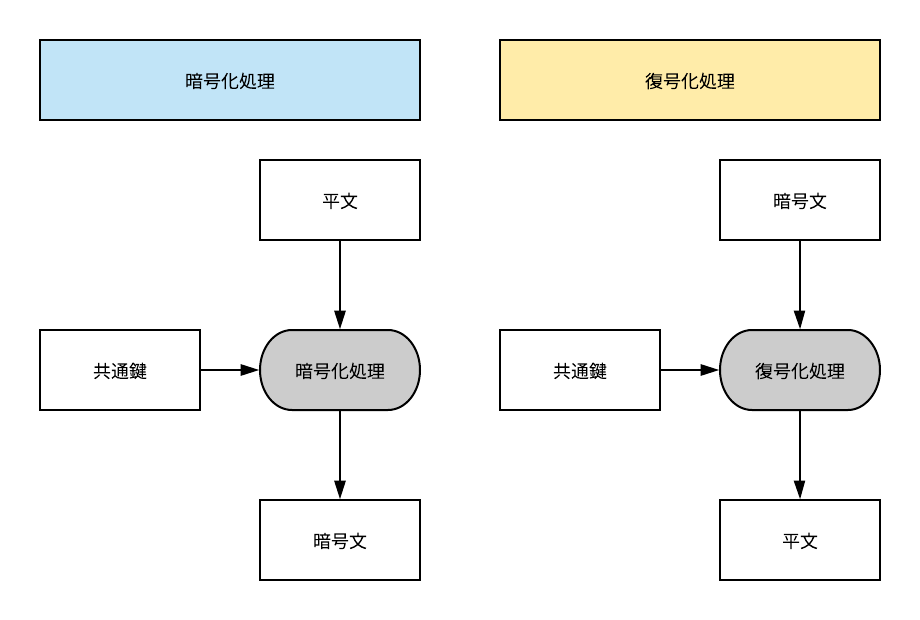
暗号化処理と復号化処理に同一の共通鍵を用いる暗号アルゴリズムである。
暗号化フロー
アルゴリズム
| 名前 | 概要 | 備考 |
|---|---|---|
| DES(Data Encryption Standard) | 64bitの平分をまとめて暗号化する技術 ファイステルネットワーク構造を用いている |
ブルートフォースアタックで現実的時間内に解読可能 |
| トリプルDES | DESによる暗号化を三回繰り返し暗号化する技術 | DESと同じあるごりずむで実装できる ただ、DESを三回繰り返すため負荷が大きく、現在はAESを使うことが一般的 |
| AES(Advanced Encryption Standard) | 128bitの平文をまとめて暗号化する技術 SPN構造を利用している |
DESの暗号強度の低下に伴い、NISTの公募により選出された暗号化技術 Rijndealというアルゴリズムを使用している |
課題
鍵配送問題
データの送受信者間で安全に鍵を共有する必要がある。
対応策
鍵配送問題
鍵配送問題を解決するには、以下の三つの方法が提案されている。
- 公開鍵暗号
- 鍵配布センターによる鍵配送問題の解決
- Diffie-Hellman(ディフィー・ヘルマン)鍵交換
本章では、公開鍵暗号を説明する。
公開鍵暗号技術
概要
暗号化と復号化に異なる鍵を用いる暗号アルゴリズムである。
暗号化の鍵を公開鍵、復号化のカギをプライベート鍵という。
- 前もって送信者に「暗号化の鍵」を送っておく。
- 受信者は「複合化の鍵」を使って複合する。
こうすれば、「複合化の鍵」を受信者に配送する必要がなくなるため、鍵配送問題を解決することが出来る。
暗号化フロー
アルゴリズム
| 名前 | 概要 | 備考 |
|---|---|---|
| RSA | 大きな数の素因数分解が困難であることを利用をした暗号化手法 | 現在最も使われている公開鍵アルゴリズムデジタル証明でも利用される |
| ElGamal方式 | mod Nの離散対数を求めることが困難なことを利用した暗号化手法 | 暗号文が平文の2倍の長さになってしまうという欠点がある |
| Rabin方式 | mod Nの平方根を求めることが困難なことを利用した暗号化手法 | |
| 楕円曲線暗号 | 楕円曲線を定め、その曲線状に乗っている点に対して特殊な「乗算」を定義する この乗算の逆演算が難しいことを利用した暗号化手法 |
RSAに対して鍵のbit数を少なくできることが特徴 |
問題点
公開鍵の認証ができない
入手した公開鍵が本当に送信者のものであるかがわからない
そのため、man-in-the-middle問題を受ける可能性がある。
上述のフローにて、盗聴者がメッセージを好きなように書き換えることができる。
対応策
公開鍵の認証ができない
公開鍵を認証する必要がある。
認証のためには、後述する証明書を利用する。
一方向ハッシュ関数
メッセージを基にハッシュ値を計算する関数のこと。
メッセージの真正性(改ざんされていないこと)のチェックに使うことができる。
一方向ハッシュ関数は以下の性質を持つ。
- 任意長のメッセージから固定長のハッシュ値を計算する
- ハッシュ値を高速に計算できる
- 一方向性を持つ
- メッセージが異なればハッシュ値も異なる
- 衝突耐性
- 弱衝突耐性
* 所与のハッシュ値と同じハッシュ値となる異なるメッセージを作成することが事実上不可能であること- 強衝突耐性
- 同じハッシュ値となる、異なる2つのメッセージのペアを求めることが事実上不可能であること
- 強衝突耐性
暗号化フロー
アルゴリズム
| 名前 | 概要 | 備考 |
|---|---|---|
| MD4 | 160bitのハッシュ値を持つ一方向ハッシュ関数 強衝突耐性が破られている |
MD変換を利用している |
| MD5 | 160bitのハッシュ値を持つ一方向ハッシュ関数 強衝突耐性が破られている |
MD変換を利用している |
| SHA-1 | 160bitのハッシュ値を持つ一方向ハッシュ関数 強衝突耐性が破られている |
MD変換を利用している |
| SHA-2 | 224bit、256bit、384bit、512bitのいづれかのハッシュ値を持つ一方向ハッシュ関数 | MD変換を利用している |
| SHA-3 | 224bit、256bit、384bit、512bitのいづれかのハッシュ値を持つ一方向ハッシュ関数 | スポンジ構造を利用している SHA-1の強衝突耐性が破られたことをきっかけに、公募により選定された KECCAKというアルゴリズムを使っている |
課題
一方項ハッシュ関数は「改ざん」を検出できるが、「なりすまし」を検出できない
一方向ハッシュ関数の送信者自体が正しい送信者であるかがどうかがわからない。
対応策
一方項ハッシュ関数は「改ざん」を検出できるが、「なりすまし」を検出できない
後述するメッセージ認証コードを利用する。
メッセージ認証コード(MAC)
鍵に依存した一方向ハッシュ関数
一方向ハッシュ関数と対称暗号を組み合わせて利用するこどで、送信者が正しい送信者であることを確認することが出来る。
暗号化フロー
アルゴリズム
先述したRSAを利用する
問題点
鍵配送問題
秘密鍵暗号同様、共通鍵を安全に共有する必要がある。
否認の防止が出来ない
お互いに共通鍵を持っているため、後々にそのメッセージ認証コードをどっちが作ったかわからない
対応策
鍵配送問題
秘密鍵暗号同様、以下の三つを利用する。
- 公開鍵暗号
- 鍵配布センター
- Diffie-Hellman鍵交換
否認の防止が出来ない
後述するデジタル署名を利用する。
デジタル署名
概要
暗号化と復号化に別のカギを使うメッセージ認証コード。
暗号化にプライベート鍵、復号化に公開鍵を使う。
暗号化フロー
デジタル署名はプライベート鍵を持っている人のみが作成できるため、真正性(正しい送信者からのメッセージであること)を担保することが出来る。
公開鍵、プライベート鍵を利用するため公開鍵暗号と似ている。
以下に、公開鍵暗号とデジタル署名の比較を記載する。
| プライベート鍵 | 公開鍵 | |
|---|---|---|
| 公開鍵暗号 | 受信者が暗号化に使う | 送信者が暗号化に使う |
| デジタル署名 | 署名者が署名の作成に使う | 検証者たちが署名の検証に使う |
課題
man-in-the-middleを受ける可能性がある
公開鍵暗号同様、通信相手を誤認する可能性がある。
対応策
man-in-the-middleを受ける可能性がある
署名を検証する際に使用する公開鍵が本人のものであることを証明する必要がある。
後述する証明書を利用する。
証明書
概要
公開鍵暗号において使用される公開鍵を、本人性(Identity)を証明するための電子データ。
公開鍵証明書とも呼ばれる。
暗号化フロー
アルゴリズム
公開鍵暗号とデジタル署名を組み合わせて利用する
課題
認証局の公開鍵の認証
上述のフローでは、認証局の公開鍵が正しいものであると判断できない
対策
認証局の公開鍵の認証
認証局の公開鍵に対して、別の認証局より証明書を作成する。
別の認証局に証明書を作成してもらう関係性より、認証局は階層状となる。
この階層の最上位の認証局をルート認証局と呼び、ルート認証局では自身の公開鍵に対して自身のプライベート鍵を用いて署名(自己署名証明書)を作成する。
まとめ
結局、これだけ覚えてればいいと思うよ。
| 担保したい性質 | 説明 | 用いる暗号化技術 |
|---|---|---|
| 機密性 | 通信内容が盗聴されないこと | 秘密鍵暗号、公開鍵暗号 |
| 真正性 (完全性) | 通信内容が改ざんされていないこと | 一方向ハッシュ関数、メッセージ認証コード、デジタル署名 |
| 認証 | 通信相手が正しい相手であること | メッセージ認証コード、デジタル署名 |
| 否認防止 | 後に自分じゃないという | デジタル署名 |