【ABC307】FortranでA,B,C問題

A - Weekly Records

問題

N週間歩いた歩数の記録について、１週間ごとにその週の合計歩数を出力します。

制約

• $1≤N≤10$
• $0≤A_i≤10^5$
• 入力は整数

詳細はこちらです。

解説

【フローチャート】

【補足】
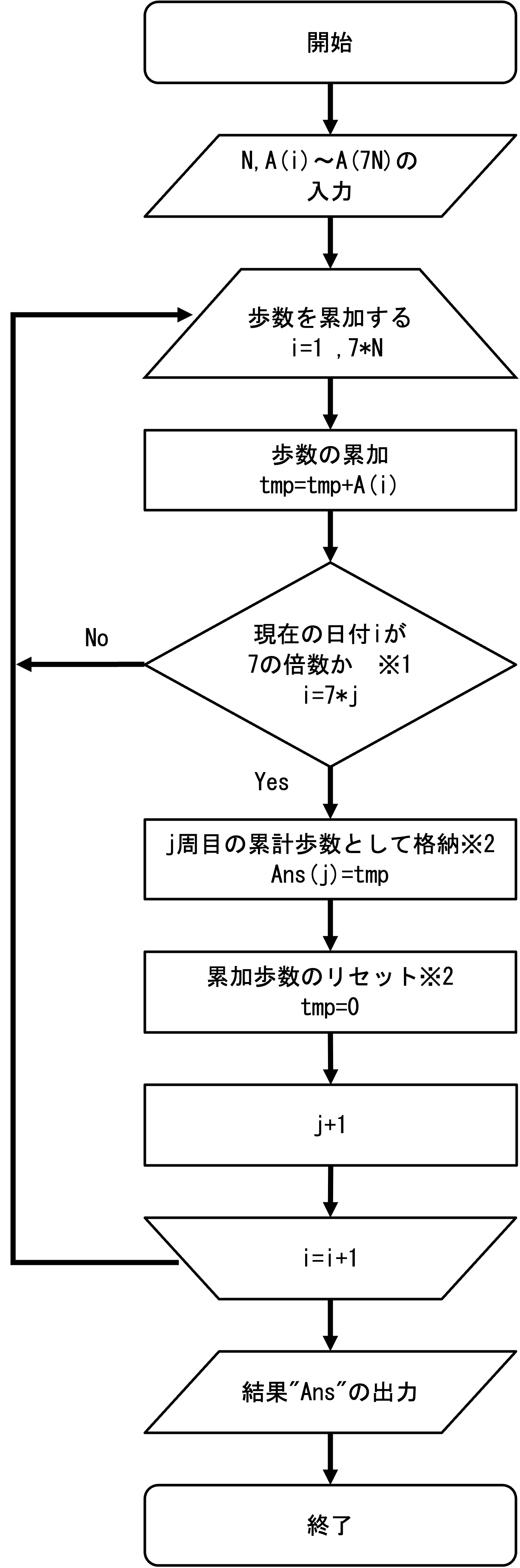
※1
ループの倍数が7の倍数になるまで、tmpに毎日の歩数を累加していきます。

※2
ループの倍数が7の倍数の時、tmpに格納されている累計歩数を1週間での合計歩数としてAns(j)に格納します。
格納後はtmp=0として、毎日の歩数を累加を再開します。

【プログラム例】

program ABC307a
    implicit none
    integer(8) i, j, tmp
    integer(8) N
    integer(8), allocatable::A(:), Ans(:)

    !初期化
    i = 0; j = 1; tmp = 0

    !入力
    read (*, *) N
    allocate (A(7*N), Ans(N))
    read (*, *) (A(i), i=1, 7*N)

    !処理
    do i = 1, 7*N
        tmp = tmp + A(i)
        if (i == 7*j) then
            Ans(j) = tmp
            tmp = 0
            j = j + 1
        end if
    end do

    !結果の出力
    write (*, *) Ans
end

B - racecar

問題

N 個の文字列 $S_1,S_2,…,S_N$ について、２つの文字列を繋げ、回文が成立する組み合わせが存在するか調べます。
回文が１つでも成立すれば"Yes"、そうでなければ"No"を出力します。

制約

• $2≤N≤100$
• $1≤S_i≤50$
• N は整数
• $S_i$ は英小文字のみからなる文字列
• $S_i$はすべて異なる。

詳細ははこちらです。

解説

【フローチャート】

【補足】
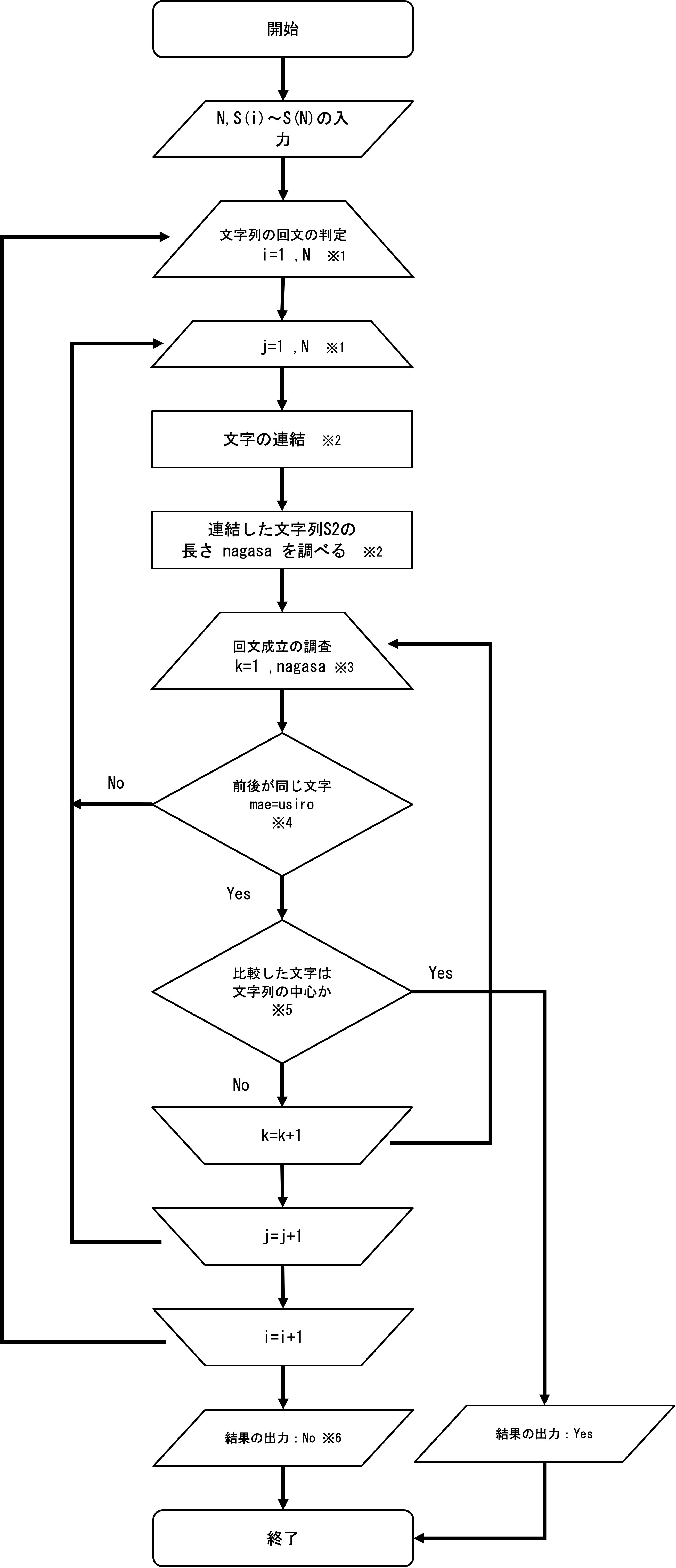
※1
2重のdo文を用いて、全ての組み合わせを調べます。

※2
S(i)とS(j)を連結しS2に格納します。
文字列の連結には、trim関数を使用します。
併せて、連結した文字の長さをlen関数を用いて調べます。

※3
回文が成立しているかどうかを１文字ずつ調べます。
調べる範囲は、文字の長さに依存し、先頭と末尾から順番に1文字ずつずらして調べていきます。

*4,5
調べる対象文字の先頭maeと末尾usiroが同じ文字かどうか調べます。
違う文字であれば、回文ではないと判断し、次の組み合わせを調べます。

同じ文字であれば、maeとusiroが文字列の中心までたどり着いているか判定します。
文字列の中心にたどり着いていなければ、maeとusiroを１文字ずらして再度同じ文字か調べます。
文字列の中心にたどり着いていれば、回文が成立しています。

*6
ループを最後まで抜けていれば、全ての組み合わせを調べても、回文が見つからなかったことになります。

【プログラム例】

program ABC307b
    implicit none
    integer(8) i, j, k, l
    integer(8) N, nagasa, guki
    character(50), allocatable :: S(:)
    character(100) S2
    character(1) mae, usiro

    !初期化
    i = 0; j = 0; k = 0

    !入力
    read (*, *) N
    allocate (S(N))
    read (*, *) (S(i), i=1, N)

    !処理
    do i = 1, N
        do j = 1, N
            if (i == j) cycle
            S2 = trim(S(i))//trim(S(j))
            nagasa = len(trim(S2))
            guki = mod(nagasa, 2)
            !write (*, '(a)') S2
            kaibun: do k = 1, nagasa
                l = nagasa + (1 - k)
                mae = S2(k:k)
                usiro = S2(l:l)
                if (mae == usiro) then
                    !write (*, '(a,1x,a)') S2(k:k), S2(l:l)
                    if (l - k == 1 .and. guki == 0) then
                        write (*, "(a)") 'Yes'
                        stop
                    else if (l - k == 2 .and. guki == 1) then
                        write (*, "(a)") 'Yes'
                        stop
                    end if
                else
                    exit kaibun
                end if
            end do kaibun
        end do
    end do

    !結果の出力
    write (*, "(a)") 'No'
end

C - Ideal Sheet

@ue1221さんが作成した、hash mapを使用しています。
この場を借りてお礼申しあげます。ありがとうございます。
([詳細についてはこちらで取り上げさせていただいています]
(https://qiita.com/onodera/items/f24b76bf5542073f6538))

問題

黒いマスと透明なマスからなるシートA,B,Xがあります。
シートA,Bを重ね合わせて、シートXが作り出せるかを検証します。
シートXが作れる場合には、"Yes"を出力します。
シートXが作れない場合には、"No"を出力します。

制約

• $1≤H_A,W_A,H_B,W_B,H_X,W_X≤10$
• $H_A,W_A,H_B,W_B,H_X,W_X$は整数
• $A_i$は . と # のみからなる長さ$W_A$の文字列
• $B_i$は . と # のみからなる長さ$W_B$の文字列
• $X_i$は . と # のみからなる長さ$W_X$の文字列
• シート A,B,X はそれぞれ少なくとも 1つ以上の黒いマスを含む。

詳細はこちらです。

解説

【フローチャート①】
解答のフローチャートは以下の通りです。
なお、『シートXが再現できているか』の処理については多重のdoループを含み複雑となるため、別図で記載しています。

【補足】
※１
do文を用いてシートA,B内の"#"の位置を記録します。
記録にはhash mapを使用します。

※2
シートA,Bの重ねた結果を格納する、シートCを定義します。
配列の定義範囲は、(-20:20,-20,20)です。
配列の範囲がシートXのサイズ(10,10)を超えているのは、
「AとBを重ねる際には、四隅を合わせて重ねる必要がなく、１マスでも重なっていれば良いためです」
例えば、A（10,10）とB(10,10)を重ねる際には、１マスでも重なっていれば良いため、重ねた後のサイズは(19,20)か(20,19)が最大サイズとなります。
従ってシートCは(-20:20,-20,20)の範囲で配列を定義します。
ただし、Xのサイズは(10,10)です。Xの再現の有無は(1:10,1:10)の範囲で行います。

※3
シートCを作成し、シートXと一致しているかを判定します。
詳細は以下のフローチャート②の通りです。
一致しているものが見つかった場合には、"Yesを出力し、プログラムを終了します。
最後まで一致する組み合わせが見つからなければ、"No"を出力します。

【フローチャート②】
『シートXが再現できているか』判定については、下記のフローチャートに従って行います。

【補足】
※4,5
シートCの作成は、シートAとシートBの位置を1マスずつ動かしながら、総当たりで考えられる全ての組み合わせを試します。
シートA,Bのどちらも２次元配列であるため、上記の実装を行うと４重のdo文になりますが$1≤H_A,W_A,H_B,W_BX≤10$と小さいため、TLEとはなりません。
そのほかの事項として、シートA,Bがどのサイズであっても、(-20:20,-20,20)と仮定して全ての組み合わせを試します。
(個別に処理を用意すると分かりにくいため。)

※6,7
シートCにシートA,Bの＃の位置をdo文を用いて書き込みます。(5重のdo文になります。)
書き込む位置は、元の＃の位置にオフセットを加えた値を書き込みます。

※8
シートXとシートCが完全に一致しているかを判定します。
判定の範囲は、※2で示した通り、(1:10,1:10)の範囲で行います。
なおこの範囲外に＃がある場合には、(1:10,1:10)の範囲が完全に一致してる場合でも"No"となります。

【プログラム例】

プログラム例(長いので折りたたんでいます。)

module mod_hash_map
    implicit none
    integer, parameter :: int_max_value = 2147483647 ! integer(4)の最大値
    integer, parameter :: default_initial_capacity = 16 ! デフォルトの初期容量
    integer, parameter :: maximum_capacity = lshift(1, 30) ! ハッシュセットに保持できる最大の要素数
    real, parameter :: default_load_factor = 0.75 ! デフォルトの負荷係数

    type t_entry ! キーと値のペアを保持するノード
        integer :: key ! キー
        integer :: val ! 値
        type(t_entry), pointer :: next => null() ! このノードに繋がっている次のノード
        integer :: hash ! ハッシュ値
    end type

    type t_entry_ptr ! ノードのポインタ
        type(t_entry), pointer :: ref => null()
    end type

    type t_hash_map ! ハッシュマップ
        ! tableはキーと値のペアのノードを管理する配列
        type(t_entry_ptr), private, allocatable :: table(:)
        integer :: size = 0
        ! thresholdはtableのサイズを大きくするかの基準
        integer, private :: threshold = int(default_initial_capacity*default_load_factor)
        ! load_factorはthresholdを決めるための負荷係数
        real, private :: load_factor = default_load_factor
    contains
        procedure :: is_empty => is_empty
        procedure :: is_not_empty => is_not_empty
        procedure :: put => put
        procedure :: get => get
        procedure :: get_or_default => get_or_default
        procedure :: remove => remove
        procedure :: clear => clear
        procedure :: contains_key => contains_key
        procedure :: contains_val => contains_val
    end type

    interface hash_map ! ハッシュマップのコンストラクタ
        module procedure :: newhm0, newhm1, newhm2
    end interface

contains

    ! ノードのコンストラクタ
    function new_entry(key, val, h) result(res)
        integer, intent(in) :: key
        integer, intent(in) :: val
        integer, intent(in) :: h
        type(t_entry), pointer :: res
        allocate (res)
        res%key = key
        res%val = val
        res%hash = h
    end

    ! integer(4)のハッシュ値を計算する関数
    ! integer(4)だとf(n) = nの形になっていて無駄に見えますが、
    ! integer(8)やreal・character等の場合は、
    ! それらの値に応じて固有のinteger(4)を計算するために必要です。
    ! 例えばinteger(8)の場合はres = xor(i, shr(i, 32))など。
    ! 注：shrは下で宣言されている関数です。
    integer function hash_code(i) result(res)
        integer, intent(in) :: i
        res = i
    end

    ! ハッシュマップのコンストラクタ
    type(t_hash_map) function newhm0() result(res)
        allocate (res%table(default_initial_capacity))
    end

    ! ハッシュマップのコンストラクタ
    type(t_hash_map) function newhm1(initial_capacity) result(res)
        integer, intent(in) :: initial_capacity
        res = newhm2(initial_capacity, default_load_factor)
    end

    ! ハッシュマップのコンストラクタ
    type(t_hash_map) function newhm2(initial_capacity, load_factor) result(res)
        integer, intent(in) :: initial_capacity
        real, intent(in) :: load_factor
        integer :: capacity
        if (initial_capacity < 0) then
            capacity = default_initial_capacity
        else
            capacity = 1
            do while (capacity < min(initial_capacity, maximum_capacity))
                capacity = lshift(capacity, 1)
            end do
        end if

        if (load_factor <= 0 .or. load_factor /= load_factor) then
            res%load_factor = default_load_factor
        else
            res%load_factor = load_factor
        end if

        res%threshold = int(capacity*res%load_factor)
        allocate (res%table(capacity))
    end

    ! ビットシフト関数(Javaの>>>に相当)
    integer function shr(i, n) result(res)
        integer, intent(in) :: i, n
        if (n == 0) then
            res = i
        else
            res = rshift(ibclr(rshift(i, 1), 31), n - 1)
        end if
    end

    ! tableのインデックスに用いるハッシュ値生成関数
    integer function hash(i) result(res)
        integer, intent(in) :: i
        integer :: h
        h = i
        h = xor(h, xor(shr(h, 20), shr(h, 12)))
        res = xor(h, xor(shr(h, 7), shr(h, 4)))
    end

    ! ハッシュ値を1~size(table)に圧縮する関数
    integer function index_for(h, length) result(res)
        integer, intent(in) :: h, length
        res = and(h, length - 1) + 1
    end

    ! ハッシュマップが空かどうか
    logical function is_empty(this) result(res)
        class(t_hash_map), intent(in) :: this
        res = this%size == 0
    end

    ! ハッシュマップに要素が1つ以上入っているかどうか
    logical function is_not_empty(this) result(res)
        class(t_hash_map), intent(in) :: this
        res = this%size /= 0
    end

    ! キーに対応する値を取り出す
    ! キーが存在しない場合は適当に0を返す
    integer function get(this, key) result(res)
        class(t_hash_map), intent(in) :: this
        integer, intent(in) :: key
        integer :: h
        type(t_entry), pointer :: e
        h = hash(hash_code(key))
        e => this%table(index_for(h, size(this%table)))%ref
        do while (associated(e))
            if (e%hash == h .and. e%key == key) then
                res = e%val
                return
            end if
            e => e%next
        end do
        res = 0
    end

    ! キーに対応する値を取り出す
    ! キーが存在しない場合はdefを返す
    integer function get_or_default(this, key, def) result(res)
        class(t_hash_map), intent(in) :: this
        integer, intent(in) :: key
        integer, intent(in) :: def
        integer :: h
        type(t_entry), pointer :: e
        h = hash(hash_code(key))
        e => this%table(index_for(h, size(this%table)))%ref
        do while (associated(e))
            if (e%hash == h .and. e%key == key) then
                res = e%val
                return
            end if
            e => e%next
        end do
        res = def
    end

    ! キーが存在するかどうか
    logical function contains_key(this, key) result(res)
        class(t_hash_map), intent(in) :: this
        integer, intent(in) :: key
        type(t_entry), pointer :: e
        e => get_entry(this, key)
        res = associated(e)
    end

    ! キーに対応するノードを取得する
    ! キーが存在しない場合はnullを返す
    function get_entry(this, key) result(res)
        class(t_hash_map), intent(in) :: this
        integer, intent(in) :: key
        integer :: h
        type(t_entry), pointer :: e
        type(t_entry), pointer :: res
        h = hash(hash_code(key))
        e => this%table(index_for(h, size(this%table)))%ref
        do while (associated(e))
            if (e%hash == h .and. e%key == key) then
                res => e
                return
            end if
            e => e%next
        end do
        res => null()
    end

    ! ハッシュマップにキーと値のペアを登録する
    ! すでにキーが存在する場合は値を新しい値に上書きする
    subroutine put(this, key, val)
        class(t_hash_map), intent(inout) :: this
        integer, intent(in) :: key
        integer, intent(in) :: val
        integer :: h, i
        type(t_entry), pointer :: e
        h = hash(hash_code(key))
        i = index_for(h, size(this%table))
        e => this%table(i)%ref
        do while (associated(e))
            if (e%hash == h .and. e%key == key) then ! すでにキーが存在する場合
                e%val = val
                return
            end if
            e => e%next
        end do
        call add_entry(this, key, val, h, i) ! ハッシュマップに新しいキーと値のペアを追加する
    end

    ! ハッシュマップに新しいキーと値のペアを追加する
    ! ハッシュが衝突した際の処理は連鎖法となっている。連鎖法については以下を参照。
    ! https://ja.wikipedia.org/wiki/%E3%83%8F%E3%83%83%E3%82%B7%E3%83%A5%E3%83%86%E3%83%BC%E3%83%96%E3%83%AB#%E9%80%A3%E9%8E%96%E6%B3%95
    subroutine add_entry(this, key, val, h, idx)
        class(t_hash_map), intent(inout) :: this !mapの名前
        integer, intent(in) :: key
        integer, intent(in) :: val
        integer, intent(in) :: h, idx
        type(t_entry), pointer :: e
        e => this%table(idx)%ref
        this%table(idx)%ref => new_entry(key, val, h)
        this%table(idx)%ref%next => e
        this%size = this%size + 1
        if (this%size >= this%threshold) call resize(this, 2*size(this%table))
    end

    ! tableがthreshold以上の個数の要素を保持している場合にtableを拡張する
    subroutine resize(this, new_capacity)
        class(t_hash_map), intent(inout) :: this
        integer, intent(in) :: new_capacity
        integer :: capacity, i, j
        type(t_entry), pointer :: e, next
        type(t_entry_ptr) :: table(new_capacity)
        capacity = size(this%table)
        if (capacity == maximum_capacity) then
            this%threshold = int_max_value
            return
        end if

        do j = 1, capacity
            e => this%table(j)%ref
            if (associated(e)) then
                this%table(j)%ref => null()
                do
                    next => e%next
                    i = index_for(e%hash, new_capacity)
                    e%next => table(i)%ref
                    table(i)%ref => e
                    e => next
                    if (.not. associated(e)) exit
                end do
            end if
        end do

        deallocate (this%table)
        allocate (this%table(new_capacity))
        do j = 1, new_capacity
            this%table(j)%ref => table(j)%ref
        end do
        this%threshold = int(new_capacity*this%load_factor)
    end

    ! キーに対応するノードを削除する
    ! キーが存在しない場合は何もしない
    subroutine remove(this, key)
        class(t_hash_map), intent(inout) :: this
        integer, intent(in) :: key
        integer :: h, i
        type(t_entry), pointer :: e, prev, next
        h = hash(hash_code(key))
        i = index_for(h, size(this%table))
        prev => this%table(i)%ref
        e => prev
        do while (associated(e))
            next => e%next
            if (e%hash == h .and. e%key == key) then
                this%size = this%size - 1
                if (associated(prev, e)) then
                    this%table(i)%ref => next
                else
                    prev%next => next
                end if
                return
            end if
            prev => e
            e => next
        end do
    end

    ! 全要素を削除する
    subroutine clear(this)
        class(t_hash_map), intent(inout) :: this
        deallocate (this%table)
        allocate (this%table(default_initial_capacity))
        this%size = 0
    end

    ! 対応する値がvalに等しいキーが存在するかどうか
    logical function contains_val(this, val) result(res)
        class(t_hash_map), intent(in) :: this
        integer, intent(in) :: val
        integer :: i
        type(t_entry), pointer :: e
        do i = 1, size(this%table)
            e => this%table(i)%ref
            do while (associated(e))
                if (e%val == val) then
                    res = .true.
                    return
                end if
                e => e%next
            end do
        end do
        res = .false.
    end
end module mod_hash_map
program ABC307c
    use mod_hash_map
    implicit none
    integer(4) i, j, cnt_a, cnt_b
    integer(4) ai, aj, bi, bj
    integer(4) nx, ny
    integer(4) min_x, max_x, min_y, max_y
    integer(4) Ha, Wa, Hb, Wb, Hx, Wx
    character(1), allocatable :: A(:, :), B(:, :), X(:, :), Ans(:, :) !配列数がn、n文字入る
    type(t_hash_map) :: Ax, Ay, Bx, By
    Ax = hash_map(); Ay = hash_map()
    Bx = hash_map(); By = hash_map()

    !初期化
    i = 0; j = 0
    cnt_a = 0; cnt_b = 0
    ai = 0; aj = 0; bi = 0; bj = 0
    nx = 0; ny = 0

    !========================
    !          入力
    !========================
    !A
    read (*, *) Ha, Wa
    allocate (A(Ha, Wa))
    do i = 1, Ha
        read (*, '(*(a1))') A(i, :)
    end do
    !B
    read (*, *) Hb, Wb
    allocate (B(Hb, Wb))
    do i = 1, Hb
        read (*, '(*(a1))') B(i, :)
    end do
    !X
    read (*, *) Hx, Wx
    allocate (X(Hx, Wx))
    do i = 1, Hx
        read (*, '(*(a1))') X(i, :)
    end do

    !========================
    !       #のカウント
    !========================
    !A
    do i = 1, Ha
        do j = 1, Wa
            if (A(i, j) == "#") then
                cnt_a = cnt_a + 1
                call Ax%put(cnt_a, j)
                call Ay%put(cnt_a, i)
            end if
        end do
    end do
    !B
    do i = 1, Hb
        do j = 1, Wb
            if (B(i, j) == "#") then
                cnt_b = cnt_b + 1
                call Bx%put(cnt_b, j)
                call By%put(cnt_b, i)
            end if
        end do
    end do

    !========================
    !      シートCの作成
    !========================
    allocate (Ans(-20:20, -20:20))
    !シートAを少しづづ動かす
    do ai = -10, 10
        do aj = -10, 10
            !シートBを少しづづ動かす
            do bi = -10, 10
                do bj = -10, 10
                    Ans = "." !Ansの初期化
                    min_x = 20; max_x = -20
                    min_y = 20; max_y = -20
                    !シートAをシートCに書き込む
                    do i = 1, cnt_a
                        nx = Ax%get(i) + aj !#のx座標+オフセット(aj)
                        ny = Ay%get(i) + ai !#のy座標+オフセット(ai)
                        Ans(ny, nx) = "#"
                        min_x = min(min_x, nx); max_x = max(max_x, nx) !シートのx範囲の最小と最大
                        min_y = min(min_y, ny); max_y = max(max_y, ny) !シートのy範囲の最小と最大
                    end do
                    !シートBをシートCに書き込む
                    do i = 1, cnt_b
                        nx = Bx%get(i) + bj
                        ny = By%get(i) + bi
                        Ans(ny, nx) = "#"
                        min_x = min(min_x, nx); max_x = max(max_x, nx)
                        min_y = min(min_y, ny); max_y = max(max_y, ny)
                    end do
                    !シートXからはみ出している位置に＃があるならNo
                    !(これをしないと、シートXの範囲で一致(部分一致)でもYesになる)
                    if (min_y < 1 .or. min_x < 1 .or. max_x > Wx .or. max_y > Hx) cycle
                    !シートXと完全一致ならYes
                    if (all(X(:, :) == Ans(1:Hx, 1:Wx))) then
                        write (*, '(a)') "Yes"
                        stop
                    end if
                end do
            end do
        end do
    end do

    !結果の出力
    write (*, '(a)') "No" !ここまで処理が通る(Yesになる組み合わせはない)のでNo
end

感想

• 今回はB問題まで解けました。 C問題は解答方法が思いつかず終了しました。
• A,B問題について、段階を踏んでデバックをした事により、WAせずに解答できました。えらい。
• フローチャートを描く練習がしたいので、次回以降の記事には図が付くと思います。
  過去の記事を含めて遡り、全ての記事でフローチャートを掲載予定です。