A - Legendary Players
問題
AtCoderのレーティング TOP 10 人のハンドルネームとレーティングが与えられます。
プレイヤーのハンドルネーム S が与えられるので、その人のレーティングを出力してください。
制約
- S はアルゴリズム部門でレーティング上位 10 人に入っているプレイヤーのハンドルネームのいずれかと等しい。
詳細はこちらです。
解説
【フローチャート】
あらかじめハンドルネームとレーティングを関連付けして登録しておき、入力したハンドルネームに応じたレーティングを出力します。

【補足】
※1
入力したハンドルネーム S と、あらかじめ登録したハンドルネームtop_name(i)が一致するかを調べます。
TOP10のハンドルネームは人によって文字列の長さが異なることに注意が必要です。
入力に使う文字型の変数 Sは10文字分用意してありますが、10文字に満たない入力がされた場合は後ろは空白が挿入されます。
S に空白が含まれている場合、一致判定の際に邪魔になるため、trim関数を用いて空白を取り除いた文字列に変換します。
プログラム例
program abc319a
implicit none
character(10) S, top_name(10)
integer top_num(10), i
!TOP10の定義
top_name(1) = 'tourist'; top_num(1) = 3858
top_name(2) = 'ksun48'; top_num(2) = 3679
top_name(3) = 'Benq'; top_num(3) = 3658
top_name(4) = 'Um_nik'; top_num(4) = 3648
top_name(5) = 'apiad'; top_num(5) = 3638
top_name(6) = 'Stonefeang'; top_num(6) = 3630
top_name(7) = 'ecnerwala'; top_num(7) = 3613
top_name(8) = 'mnbvmar'; top_num(8) = 3555
top_name(9) = 'newbiedmy'; top_num(9) = 3516
top_name(10) = 'semiexp'; top_num(10) = 3481
!読み込み、結果の出力
read (*, *) S
do i = 1, 10
if (trim(S) == top_name(i)) then
write (*, '(i0)') top_num(i)
stop
end if
end do
end program abc319a
B - Measure
問題
正整数 N が与えられるので、下記で定まる長さ (N+1) の文字列 $s_0,s_1,…s_N$を出力してください。
$S_i$の計算
- 1 以上 9 以下の N の約数 j であって、i が N/j の倍数であるものが存在するとき、
そのような j のうち最小のものに対応する数字を $s_i$ とする。- 上記の条件を満たす j が存在しないとき、$s_i$は - とする。
制約
- $1≤N≤1000$
- 入力はすべて整数
詳細はこちらです。
解説
【フローチャート】
$S_1$から$S_N$まで総当たりで計算します。
$S_0とS_N$はNがどんな数であっても必ず1になります。
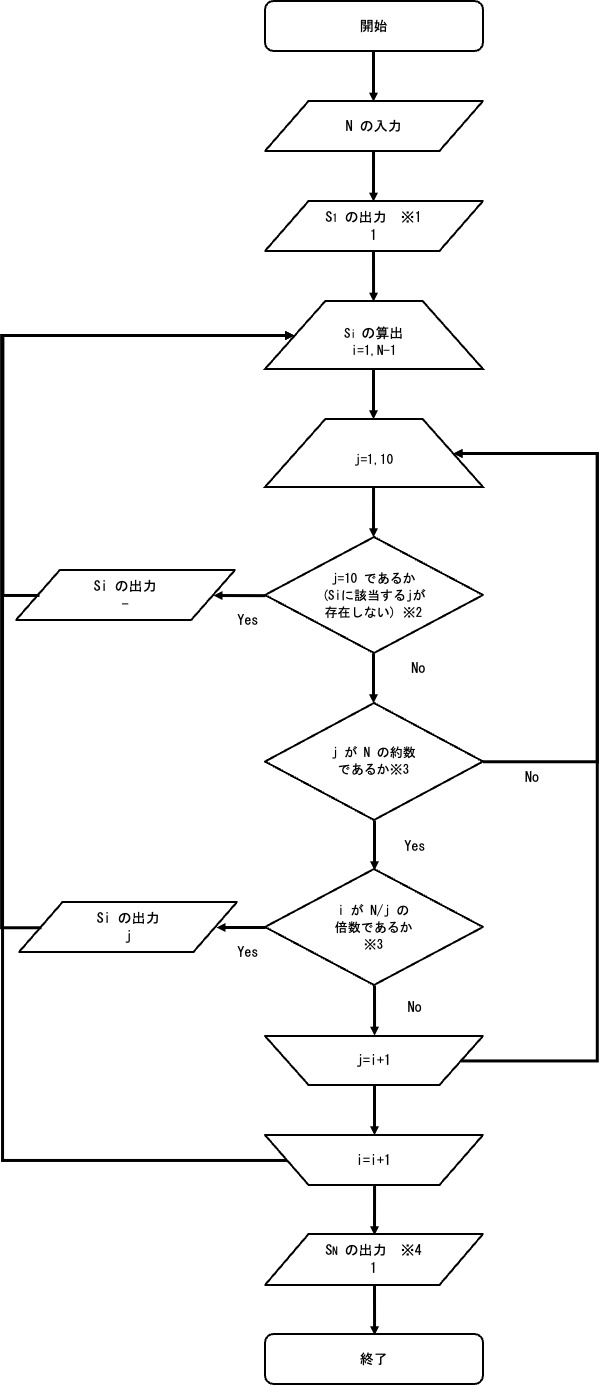
【補足】
※1
$i=0$の時は $N$ がどのような数であっても$S_0=1$となります。
以降の処理で$S_i$を求めますが $i=0$の時は計算する必要がないので、$S_0$をあらかじめ出力します。
※2
$j=1〜9$の範囲内に$S_i$ の条件を満たす $j$ が見つからない場合があります。
この場合は - を出力します。
プログラム上$はj=1〜10$までループの範囲をとり、
$j=10$になった時点で$S_i$ の条件を満たす $j$ はないと判定します。
※3
$S_i$の条件を満たすか判定します。
$j=1$から昇順にループを回しているので、最初に条件を満たした$j$が最小の$S_i$となります。
※4
$i=N$の時は $N$ がどのような数であっても$S_N=1$となります。
$i=N$の時は計算する必要がないので、$S_N$はループの終了後に出力します。
プログラム例
program abc319b
implicit none
integer N, i, j
!読み込み
read (*, *) N
!処理
write (*, '(i0)', advance='no') 1
do i = 1, N - 1
do j = 1, 10
if (j == 10) then
write (*, '(a)', advance='no') '-'
exit
end if
if (mod(N, j) == 0) then
if (mod(i, N/j) == 0) then
write (*, '(i0)', advance='no') j
exit
end if
else
cycle
end if
end do
end do
!結果の出力
write (*, '(i0)', advance='no') 1
end program abc319b
C - False Hope
問題
3×3 のマス目に 1 から 9 までの数字が書き込まれています。
同じ数字が縦・横・斜めに 3 つ連続して書き込まれていることはありません。
それぞれのマスに書かれている数字をランダムな順番で知ります。
縦・横・斜めの列のうちの 1 つでも次の条件を満たしたときがっかりします。
条件
はじめに知ったほうの 2 マスに書かれた数字が同じであり、最後に知ったマスに書かれた数字がそれと異なる。
がっかりせずに全てのマスを知る確率を求めてください。
制約
- $c_{i,j} ∈{1,2,3,4,5,6,7,8,9} (1≤i≤3,1≤j≤3)$
- $c_{i,1}=c_{i,2}=c_{i,3}ではない(1≤i≤3)$
- $c_{1,j}=c_{2,j}=c_{3,j}ではない(1≤j≤3)$
- $c_{1,1}=c_{2,2}=c_{3,3}ではない$
- $c_{1,3}=c_{2,2}=c_{3,1}ではない$
詳細はこちらです。
解説
【注意点】
数字を知る順番は$362880$通りあり、1枚めくる度にがっかりしたか調べているとTLEとなってしまします。
【フローチャート】
3×3 のマス目に対し左上から順番に1~9の番号を振り、1次元配列にして「めくる順番と数字」を管理します。
めくる順番をソートして整理し、がっかりする判定にならないかを確かめます。

【補足】
※1
がっかりするかの判定を行います。
めくる順番をソートして整理し、がっかりする判定になるかを確かめます。
がっかりする判定になるかをチェックする必要のある組み合わせは、以下に示すタテ、ヨコ、ナナメの8種類です。
チェックする組み合わせ
- $1,2,3$
- $4,5,6$
- $7,8,9$
- $1,4,7$
- $2,5,8$
- $3,6,9$
- $1,5,9$
- $3,5,7$
上記の組み合わせのうち、どれか1つでも満たせばがっかりする判定になります。
題意よりがっかりしたあとに次の数字を知ることはないので、複数のがっかりする判定を満たしている場合でもカウントする数は1になります。
※2
数字を知る順番は$362880$通りあります。
next_permutationを用いて数字を知る順番の組み合わせを生成します。
全ての組み合わせを生成し終えた場合、do文を終了します。
プログラム例
module ABC319c_mod
implicit none
! グローバル変数
integer arr(9), order(9)
real(16) ans, cnt
end module
program abc319c
use ABC319c_mod
implicit none
integer i
logical check, check2
integer C(3, 3)
!入力
do i = 1, 3
read (*, *) C(i, :)
end do
!
arr(1:3) = C(1, 1:3); arr(4:6) = C(2, 1:3); arr(7:9) = C(3, 1:3)
order = (/1, 2, 3, 4, 5, 6, 7, 8, 9/)
!がっかりする回数の測定
check = .false.; cnt = 0d0
do
!がっかりするかを判定
check2 = .false.
call check_gakkari(1, 2, 3, check2); call check_gakkari(4, 5, 6, check2); call check_gakkari(7, 8, 9, check2)
call check_gakkari(1, 4, 7, check2); call check_gakkari(2, 5, 8, check2); call check_gakkari(3, 6, 9, check2)
call check_gakkari(1, 5, 9, check2); call check_gakkari(3, 5, 7, check2)
!次の組み合わせを計算
call next_permutation(order, 9, check)
if (check .eqv. .true.) exit
end do
!結果の出力
ans = 1d0 - cnt/362880d0
write (*, *) ans
contains
subroutine next_permutation(order, n, check)
integer n, k, kari, order(n), tmp(n), i, l
logical check
do k = n - 1, 1, -1
if (order(k) < order(k + 1)) exit
if (k == 1) then
check = .true.
exit
end if
end do
do l = n, k + 1, -1
if (order(k) < order(l)) exit
end do
kari = order(k); order(k) = order(l); order(l) = kari
if (k + 1 /= n) then
do i = 1, k
tmp(i) = order(i)
end do
do i = 0, n - (k + 1)
tmp(n - i) = order(k + 1 + i)
end do
order = tmp
end if
end subroutine
subroutine check_gakkari(o1, o2, o3, check2)
integer o1, o2, o3
integer x(3), y(3), tmp(3), tmp2(3)
logical check2
tmp = 0; tmp2 = 0
if (check2 .eqv. .true.) return
x(1) = order(o1); x(2) = order(o2); x(3) = order(o3)
y(1) = arr(o1); y(2) = arr(o2); y(3) = arr(o3)
call margesort(x, y, tmp, tmp2, 3, 1, 3)
if (y(1) == y(2)) then
cnt = cnt + 1d0
check2 = .true.
end if
end subroutine
recursive subroutine margesort(x, y, tmp, tmp2, N, left, right)
integer left, right, mid
integer i, j, k, N
integer x(N), tmp(N), y(N), tmp2(N)
if (left >= right) return
mid = (left + right)/2
call margesort(x, y, tmp, tmp2, N, left, mid)
call margesort(x, y, tmp, tmp2, N, mid + 1, right)
j = 0
tmp(left:mid) = x(left:mid)
tmp2(left:mid) = y(left:mid)
do i = mid + 1, right
tmp(i) = x(right - j)
tmp2(i) = y(right - j)
j = j + 1
end do
i = left
j = right
do k = left, right
if (tmp(i) < tmp(j)) then
x(k) = tmp(i)
y(k) = tmp2(i)
i = i + 1
else if (tmp(i) == tmp(j)) then
x(k) = tmp(i)
y(k) = tmp2(i)
i = i + 1
else
x(k) = tmp(j)
y(k) = tmp2(j)
j = j - 1
end if
end do
end subroutine margesort
end
感想
- 自前の
next_permutationサブルーチンを使う機会が増えてうれしい