目次
A - Spread
問題
文字列 S が与えられます。S の各文字を空白で区切り、その順で 1 文字ずつ出力します。
制約
- S は長さ 2 以上 100 以下の英大文字からなる文字列
詳細はこちらです。
解説
【フローチャート】

【補足】
※1
出力したい文字の次の文字が存在するかどうかによって処理を分岐させます。
※2
1文字ごとに改行を行う必要はありません。
write文にadvance='noを追加し、改行が行われないようにします。
※3
最後の文字の後ろには空白を出力しません。
別途処理を分け、最後の文字の後ろには空白を出力しないようにします。
プログラム例
program abc329a
!S:文字列
implicit none
integer i
character(100) S
!入力
read (*, *) S
!結果の出力
do i = 1, 100
if (S(i + 1:i + 1) == '') then
write (*, '(a1)') S(i:i)
stop
else
write (*, '(a1,1x)', advance='no') S(i:i)
end if
end do
end program abc329a
B - Next
問題
N 個の整数 $A_1 ,A_2,…,A_N$ が与えられます。
このうち2番目に大きい数を求めてください。
制約
- $1≤N≤100$
- $1≤A_i≤100$
- A_1 ,A_2 ,…,A_N がすべて等しいということはない
詳細はこちらです。
解説
【フローチャート】
総当たりで条件を満たす整数を探します。
あらかじめ A をソートしておき、少ない計算量で2番目に大きい数を探します。
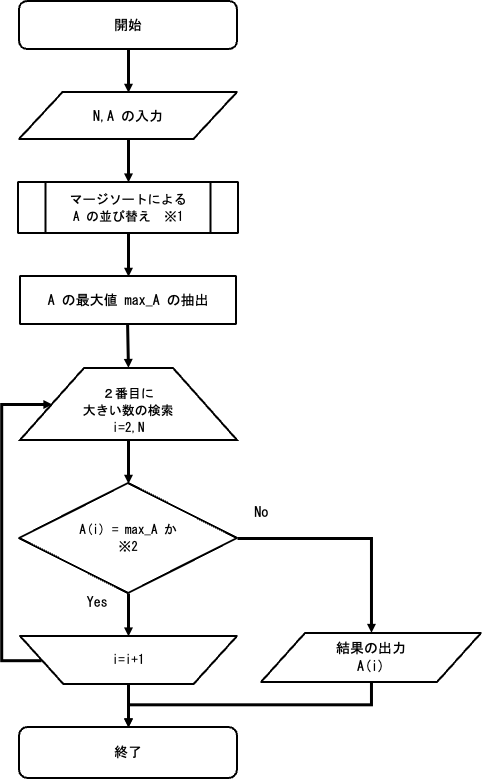
【補足】
※1
最大値、2番目に大きい値を効率的に探すために、前処理としてAを降順にソートしておきます。
※2
A(2)から順番に値を確認し、A(1) と違う値であるかを確認します。
A は降順にソートされているので、$A(1) \neq A(i)$であれば2番目に大きい値とすることができます。
プログラム例
program abc329b
!N :整数の総数
!A :整数(A1,A2,...AN)
!max_A:
implicit none
integer(16) N, i, max_A
integer(16), allocatable :: A(:)
!入力
read (*, *) N
allocate (A(N))
read (*, *) A
!ソート
call margesort(A, N)
!出力
max_A = A(1)
do i = 2, N
if (max_A /= A(i)) then
write (*, '(i0)') A(i)
stop
end if
end do
contains
subroutine margesort(x, n)
integer(16) N
integer(16) x(N), tmp(N)
integer(16) start, end
start = 1; end = N
call loop_margesort(x, tmp, N, start, end)
end subroutine
recursive subroutine loop_margesort(x, tmp, N, left, right)
integer(16) left, right, mid
integer(16) N
integer(16) x(N), tmp(N)
character(1) y(N), tmp2(N)
integer(16) i, j, k
!これ以上2分かつできないならretrun
if (left >= right) return
!分割できるだけ分割する
mid = (left + right)/2
call loop_margesort(x, tmp, N, left, mid)
call loop_margesort(x, tmp, N, mid + 1, right)
!並び替えの下準備としてtmpに配列をコピー
j = 0
tmp(left:mid) = x(left:mid)
tmp2(left:mid) = y(left:mid)
do i = mid + 1, right
tmp(i) = x(right - j)
tmp2(i) = y(right - j)
j = j + 1
end do
!大小比較して小さい順に入れていく
i = left
j = right
!write (*, '(3x,*(f13.101x),a)', advance='no') x(left:right)
!write (*, '(a)', advance='no') '>>'
do k = left, right
if (tmp(i) > tmp(j)) then
x(k) = tmp(i)
y(k) = tmp2(i)
i = i + 1
else if (tmp(i) == tmp(j) .and. tmp2(i) < tmp2(j)) then
x(k) = tmp(i)
y(k) = tmp2(i)
i = i + 1
else
x(k) = tmp(j)
y(k) = tmp2(j)
j = j - 1
end if
end do
!write (*, '(3x,*(f13.10,1x))') x(left:right)
end subroutine loop_margesort
end program abc329b
C - Count xxx
問題
英小文字からなる長さ N の文字列 S が与えられます。
S の中で、 1 種類の文字で表現できる文字列の組み合わせを求めます。
制約
- $1≤N≤2×10^5$
- S は英小文字からなる長さ N の文字列
詳細はこちらです。
解説
【フローチャート】
あらかじめ S を 1 文字目から順番に確認し、どこでどれだけ同じ文字が連続しているかを調べ、その最大値を記録しておきます。
各文字の識別にはアスキーコードを使用し、文字を数字に変換して識別します。

【補足】
※1
A~Z の出現回数を配列に格納して管理する際、配列の添字は数字である必要があります。
今回はアスキーコードを使って A~Z の文字を数字に変換します。
変換にはiachar関数を使用します。
※2
i 文字の右隣の文字が同じ文字かを判定します。
同じであれば、1 種類の文字で表現できる文字列として扱えるので、連続している回数のカウントを増やします。
※3
カウントした回数が、その種類の文字の最大の連続回数であれば、値を更新します。
プログラム例
program abc329c
!N :文字列の長さ
!S :文字列
!ascll:各文字の連続回数の最大値を記録(97:a, 122:z)
!cnt :各文字の連続回数を一時保存
!tmp :Sの各文字をアスキー文字に変換した結果
implicit none
integer N, tmp, cnt, i, j
integer ascll(122)
character(:), allocatable::S
!入力
read (*, *) N
allocate (character(N)::S)
read (*, *) S
!集計
ascll = 0
i = 1
do
tmp = iachar(S(i:i))
!初回カウント
if (ascll(tmp) == 0) then
ascll(tmp) = ascll(tmp) + 1
end if
!連続カウント
cnt = 1
do j = i + 1, N
if (iachar(S(j:j)) == tmp) then
cnt = cnt + 1
else
exit
end if
end do
!MAX更新
if (ascll(tmp) < cnt) then
ascll(tmp) = cnt
end if
i = j
if (i > N) exit
end do
!結果出力
cnt = 0
do i = 97, 122
cnt = ascll(i) + cnt
end do
write (*, *) cnt
end program abc329c
感想
- A:5分、B:10分、C:72分でした。