目次
A - Not Too Hard
問題
N 問の問題が出題されるプログラミングコンテストがあります。 $i=1,2,…,N$ について、i 問目の配点は $S_i$ です。
配点が X 以下である問題すべての配点の合計を出力しします。
制約
- 入力される値は全て整数
- $4≤N≤8$
- $100≤S_i≤675$
- $100≤X≤675$
詳細はこちらです。
https://atcoder.jp/contests/abc328/tasks/abc328_a
解説
【フローチャート】
N 問の問題を総当たりで調べ、配点が X 以下であるかを判定します。
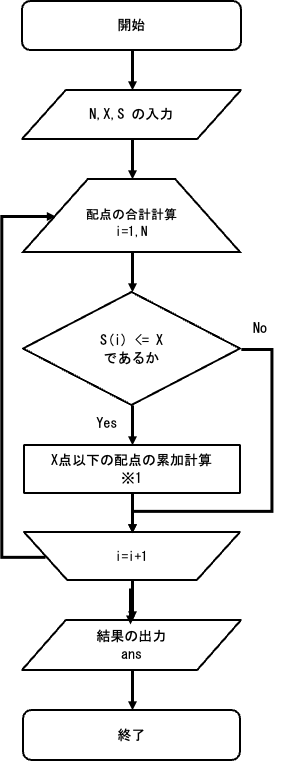
【補足】
※1
i 問の問題の配点が X 以下である場合は、変数ansに i 問目の配点を加えます。
プログラム例
program abc328a
!N:問題数
!S:各問題の配点
!X:集計したい配点の閾値
!ans:X点以下の問題の配点の合計
implicit none
integer(16) N, X, i, ans
integer(16), allocatable :: S(:)
!入力
read (*, *) N, X
allocate (S(N))
read (*, *) S
!配点の合計計算
ans = 0
do i = 1, N
if (S(i) <= X) then
ans = ans + S(i)
end if
end do
!結果の出力
write (*, '(i0)') ans
end program abc328a
B - 11/11
問題
1年が N か月、1か月が $D_i,D_2,...D_N$ 日からなる国があります。
1年間のうち、月日がゾロ目になる日数の合計を求めます。
制約
- $1≤N≤100$
- $1≤D_i ≤100 (1≤i≤N)$
- N は整数である
詳細はこちらです。
解説
【フローチャート】
総当たりで 1年間の全日数を調べ、ゾロ目になる日の合計を求めます。
月 i と日付 j が 1 桁の場合は i==j でゾロ目の判定ができます。
月 i と日付 j が 2 桁以上になった場合には、 1 桁目と 2 桁目に分解して比較する必要があります。
警告
回答が多重のif文で構成されているます。
解法として不適切な部分があることから、詳細な解説は省略します。
プログラム例
program abc328b
!N :1年の月数
!D :各月の日数
!m3 :各月の1,2,3桁目の数
!d3 :各日の1,2,3桁目の数
!ans:月日がゾロ目になる合計回数
implicit none
integer(16) N, i, j, ans, d3(3), m3(3)
integer(16), allocatable :: D(:)
!入力
read (*, *) N
allocate (D(N))
read (*, *) D
!判定
ans = 0
do i = 1, N
if (i == 100) cycle
do j = 1, D(i)
if (j == 100) cycle
!1桁
if (i < 10) then
if (j < 10 .and. j == i) then
ans = ans + 1
!write (*, *) i, j
else
d3(3) = j/100
d3(2) = j/10 - d3(3)*10
d3(1) = j - d3(3)*100 - d3(2)*10
if (d3(1) == i .and. d3(2) == i) then
ans = ans + 1
!write (*, *) i, j
end if
end if
else
m3(3) = i/100
m3(2) = i/10 - m3(3)*10
m3(1) = i - m3(3)*100 - m3(2)*10
if (m3(1) == m3(2)) then
if (j < 10 .and. m3(1) == j) then
ans = ans + 1
!write (*, *) i, j
else
d3(3) = j/100
d3(2) = j/10 - d3(3)*10
d3(1) = j - d3(3)*100 - d3(2)*10
if (d3(1) == m3(1) .and. d3(2) == m3(1)) then
ans = ans + 1
!write (*, *) i, j
end if
end if
end if
end if
end do
end do
!出力
write (*, '(i0)') ans
end program abc328b
C - Consecutive
問題
長さ N の文字列 S が与えられます。
S に関する Q 個の質問が与えられます。
質問は、S の 「 $l_i$ から $r_i$ 文字目までに 同じ文字が隣接する箇所は何箇所あるか」という内容です。
$l_i$ 、 $r_i$ は各質問により異なります。
各質問のそれぞれの答えを求めて出力します。
制約
- N,Q は整数
- $1≤N,Q≤3×10^5$
- S は英小文字のみからなる長さ N の文字列
- $l_i,r_i$ は整数
- $1≤l_i≤r_i≤N$
詳細はこちらです。
解説
【フローチャート】
$1≤N,Q≤3×10^5$ であるため、質問の度に$l_i$ から $r_i$ 文字目まで隣接する文字を調べるとTLEとなります。
あらかじめ S を全範囲調べ、同じ文字が隣接する箇所を調べておきます。
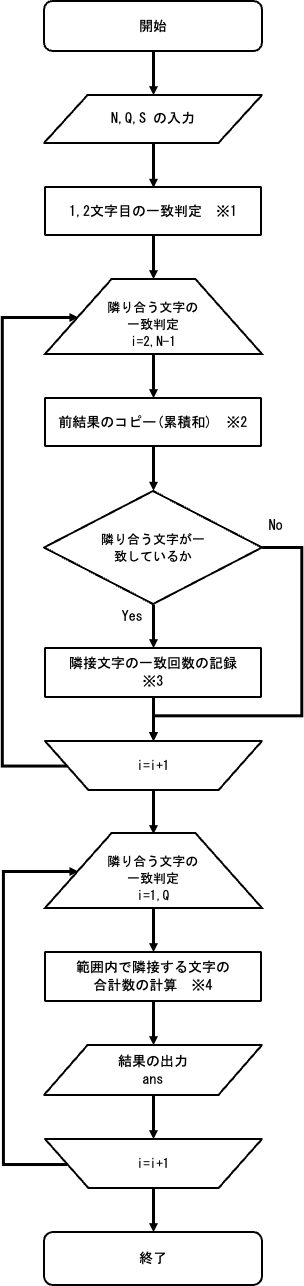
【補足】
※1
以降の処理では、1つ前の隣接する文字の判定結果を使用します。
後の処理のために、あらかじめ1,2文字目が一致するかの判定を行います。
※2
累積和を用いて、i 文字目までに隣接する文字の判定結果を記録します。
累積和の計算は1つ前の計算結果を用いて、増減分のみを計算します。
do文の始点が i=2となっているのは、 i=1 から始める場合、1つ前の結果が存在しないためです。
i=1 のケースは ※1 で計算します。
※3
※2の結果を用いて質問 $Q_i$ の結果を出力します。
結果を出力したい範囲の開始点は、必ずしも 1 文字目にはならないので、$R_i$ 文字目と $L_i$ 文字目の結果の差分を取る必要があります。
プログラム例
program abc328c
!S :文字列
!N :Sの文字数
!Q :Sに関する質問の数
!R :隣り合う文字の一致判定をしたい範囲の始点
!L :隣り合う文字の一致判定をしたい範囲の終点
!cnt:隣り合う文字の一致個数
!ans:各質問ごとに集計した隣り合う文字の一致個数
integer N, Q
integer, allocatable::cnt(:)
character(:), allocatable::S
integer ans
integer, allocatable::R(:), L(:)
!入力
read (*, *) N, Q
allocate (character(N)::S)
allocate (R(Q), L(Q), cnt(N))
read (*, *) S
do i = 1, Q
read (*, *) L(i), R(i)
end do
!隣り合う文字の一致判定
cnt = 0
if (S(1:1) == S(2:2)) cnt(1) = 1
do i = 2, N - 1
cnt(i) = cnt(i - 1)
if (S(i:i) == S(i + 1:i + 1)) cnt(i) = cnt(i) + 1
end do
!結果の出力
ans = 0
do i = 1, Q
ans = cnt(R(i) - 1) - cnt(L(i) - 1)
write (*, '(i0)') ans
end do
end program abc328c
感想
- A:3分、B:30分でした。
- C問題、全範囲の結果をあらかじめ計算しておくところまでは思いついたのですが、それを累積和にする発想が思いつきませんでした。解放の切り分けが今後の課題です。
