リスト探索（C言語）

探索とは

データ列の中に要素$x$があるか探すこと
特に、リスト探索はデータ列（リスト）から何らかのキーを持つ要素を見つけることが目的

線形探索

線形探索とは

リストの各要素を見て、要素$x$があるか探す。

サンプルコード

liner_sort.c

#include<stdio.h>

/* 線形探索（ソートされていなくても使える）*/
int liner_search (int list[], int list_size, int x) {
  int i = 0;
  while (i < list_size) {
    if (list[i] == x) { return i; }
    i++;
  }
  return -1;
}

/* 線形探索（ソート済みの時使える）*/
int sorted_liner_search (int list[], int list_size, int x) {
  int i = 0;
  while (i < list_size) {
    if (list[i] == x) { return i; }
    if (list[i] > x) { break; }  // これ以降にxがある可能性はないので打ち切り
    i++;
  }
  return -1;
}

int main (void) {
  int list[10] = {0, 4, 9, 10, 13, 17, 25, 36, 37, 40};
  int x;
  int answer;

  printf("x?> ");
  scanf("%d", &x);
  answer = liner_search(list, 10, x);
  if (answer != -1) { printf("%d\n", answer); }
  else              { printf("not exist\n"); }

  printf("x?> ");
  scanf("%d", &x);
  answer = sorted_liner_search(list, 10, x);
  if (answer != -1) { printf("%d\n", answer); }
  else              { printf("Not exist\n"); }
}

実行結果

x?> 5
not exist
x?> 4
1

サンプルではlistはソート済みの配列なので、sorted_liner_search()もつかえる。

性能

• 時間計算量$O(n)$
• 比較回数
  • 探索不成功：$N+1$回
  • 探索成功：平均$N/2$回
• 整列済みの場合、sorted_liner_search()を用いると、探索が不成功の時でも平均$N/2$回の比較で済む

二分探索

二分探索とは

整列済みのデータを二分し、要素$x$がある可能性のある部分データをまた二分し、という操作を繰り返す
例えば、整数が並んでいるデータ列の中から10を見つける場合、データ列の真ん中が5だったら後半を探し、データ列の真ん中が20だったら前半を探し$\cdots$という感じ

サンプルコード

binary_search.c

#include<stdio.h>

/* 二分探索 */
int binary_search (int list[], int list_size, int x) {
  int left, right, mid;
  left = 0;
  right = list_size - 1;

  while (left <= right) {
    mid = (left + right)/2;
    if (list[mid] == x) { return mid; }
    else if (list[mid] < x) { left = mid + 1; }
    else                    { right = mid - 1; }
  }
  return -1;
}

int main (void) {
  int list[10] = {0, 4, 9, 10, 13, 17, 25, 36, 37, 40};
  int x;
  int answer;

  printf("x?> ");
  scanf("%d", &x);
  answer = binary_search(list, 10, x);
  if (answer != -1) { printf("%d\n", answer); }
  else              { printf("not exist\n"); }

}

実行結果

$ ./binary_search
x?> 9
2
$ ./binary_search
x?> 78
not exist

性能

• 時間計算量$O(\log_2n)$
• 比較回数$\log_2(n+1)$以下
• 比較回数の上限$C_n=C_{n/2}+1$

内挿探索

内挿探索とは

データが整列済みで一様に分布しているとすると、単純に「真ん中」よりも内挿した位置を見るほうが効率がいい
電話帳で「阿部さん」を探す時は、真ん中ではなく、先頭の方を見るのとおんなじ

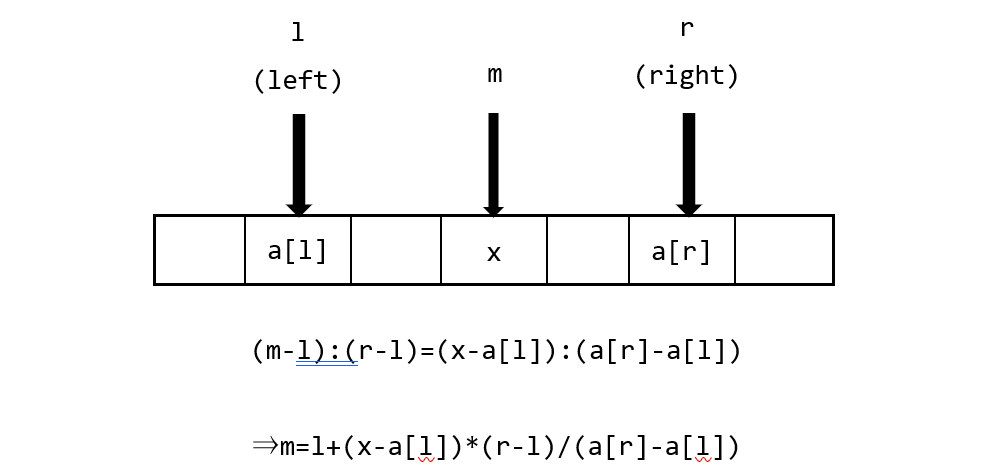
データが一様に分布しているとすると、データ列の番号（配列の添え字）とデータの値（配列の中身）は大体比例するので、区間$[l,m]$と$[m,r]$の比を考えて、$a[m]\fallingdotseq x$となる$m$を選ぶ。

サンプルコード

注意：次のコードはxの値がlist[0]とlist[10]の範囲に入っていることが前提

interpolation_search.c

#include<stdio.h>

/* 内挿探索 */
int interpolation_search (int list[], int list_size, int x) {
  int left, right, mid;
  left = 0;
  right = list_size - 1;

  while (left <= right) {
    if (left == right) { mid = left; }
    else { mid = left + (x - list[left])*(right - left)/(list[right] - list[left]); }
    if (list[mid] == x) { return mid; }
    else if (list[mid] < x) { left = mid + 1; }
    else                    { right = mid - 1; }
  }
  return -1;
}

int main (void) {
  int list[10] = {0, 4, 9, 10, 13, 17, 25, 36, 37, 40};
  int x;
  int answer;

  printf("x?> ");
  scanf("%d", &x);
  answer = interpolation_search(list, 10, x);
  if (answer != -1) { printf("%d\n", answer); }
  else              { printf("not exist\n"); }

}

実行結果

$ a.exe
x?> 5
not exist
$ a.exe
x?> 25
6

性能

データが一様分布なら理論上は二分探索よりも高速だが、$m$を求める計算コストが高いので、実際には要素数$n$がかなり大きくない限り二分探索より遅くなることが多い。