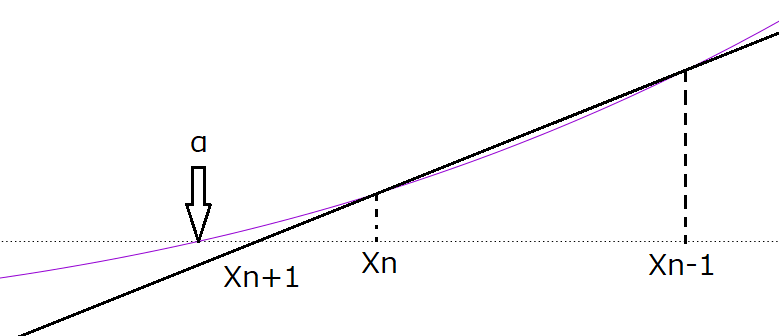割線法（非線形方程式の数値解法）

割線法とは

• 非線形方程式の数値解法の一つ
• Newton法では、一階の微係数が必要だが、方程式によってはこの計算はしばしば困難
• 微係数を数値的に求める

算法

初期値

$x_0,x_1$ : 適当な方法で決める

反復手順

$x_{n+1}=x_n-f(x_n)\frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}$

停止則

• 更新量が小さい：$|f(x_n)\frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}|<\varepsilon_1$
• $f(x_n)$が$0$に近い：$|f(x_n)|<\varepsilon_2$

サンプルコード

$f(x)=x^2-1$ 、初期値 $x_1=0.5,x_1=2$ として割線法を使って解を求めるプログラム。
$f(x_n)-f(x_{n-1})\neq 0$の確認とかを入れてないガバガバコード

secant_method.c

# include<stdio.h>
# include<math.h>

double f (double x) {
  return x*x-1;
}

double df (double x_1, double x_2) {
  return (x_1 - x_2)/(f(x_1) - f(x_2));
}

double secant_method (double x_n, double x_n_1) {
  double new_x;
  while (1) {
    new_x = x_n - f(x_n)*df(x_n, x_n_1);
    if (fabs(f(x_n)*df(x_n, x_n_1)) < 1e-10) break;
    if (fabs(f(new_x)) < 1e-10) break;
    x_n_1 = x_n;
    x_n = new_x;
  }
  return new_x;
}

int main (void) {
  double alpha;
  alpha = secant_method(0.5, 2);
  printf("%f\n", alpha);
  return 0;
}

実行結果

1.000000

特徴

• $f^{\prime}(x)$の計算不要
  • $f^{\prime}(x)$が煩雑で微係数の計算が困難な時に有効
• 初期値二つ必要
  • 初期値によってはうまく収束しない
• Newton法に比べ、反復回数が増加