C言語でマージソート

マージソートとは

分割統治法に基づくアルゴリズム

手順

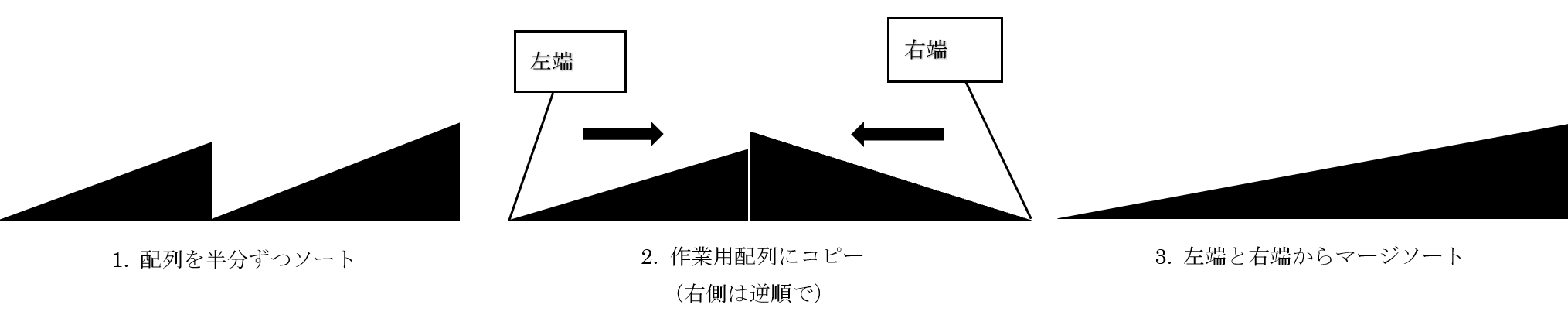
1. 与えられた配列（長さ$n$）を$n/2$の部分配列に分割
2. 2つの部分配列をそれぞれマージソート
3. 得られた二つのソート済み部分配列を統合

基本的な考え方

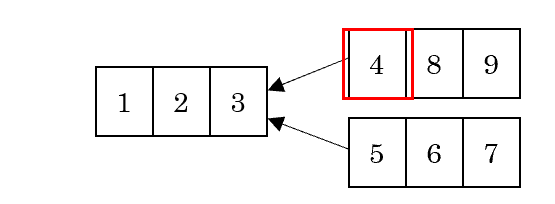
• 整列済みの2つの配列を併合する
• 2つの配列の先頭を見て、小さいほうを取り出す
• 配列の併合を再帰的に実行

サンプルコード

int型の配列を、マージソートを用いて整列するプログラム

merge_sort.c

#include<stdio.h>

/* マージソート */
void merge_sort (int array[], int left, int right) {
  int i, j, k, mid;
  int work[10];  // 作業用配列
  if (left < right) {
    mid = (left + right)/2; // 真ん中
    merge_sort(array, left, mid);  // 左を整列
    merge_sort(array, mid+1, right);  // 右を整列
    for (i = mid; i >= left; i--) { work[i] = array[i]; } // 左半分
    for (j = mid+1; j <= right; j++) {
      work[right-(j-(mid+1))] = array[j]; // 右半分を逆順
    }
    i = left; j = right;
    for (k = left; k <= right; k++) {
      if (work[i] < work[j]) { array[k] = work[i++]; }
      else                   { array[k] = work[j--]; }
    }
  }
}

int main (void) {
  int array[10] = { 2, 1, 8, 5, 4, 7, 9, 0, 6, 3 };
  int i;

  printf("Before sort: ");
  for (i = 0; i < 10; i++) { printf("%d ", array[i]); }
  printf("\n");

  merge_sort(array, 0, 9);

  printf("After sort: ");
  for (i = 0; i < 10; i++) { printf("%d ", array[i]); }
  printf("\n");

  return 0;
}

実行結果

Before sort: 2 1 8 5 4 7 9 0 6 3
After sort: 0 1 2 3 4 5 6 7 8 9

性能

• 比較回数$O(n\log{n})$で実用的
• 作業領域が必要
• 安定ソート
• 性能は、入力のデータの並び方に影響されない