片対数グラフを使って,$y=Ca^{x}$の関係にあるデータの,$C$や$a$を求める方法のメモ.
$y=e^{x}$を例に,片対数グラフから底$e=2.718...$を求めてみます.
手順
1. 片対数グラフにデータをプロット
2. 直線の傾き・切片を読み取る
3. 指数の底やべきを求める
手順1 片対数グラフを用意
$y=e^{x}$のデータとグラフを作ります.
実際は,次に示すグラフが実験などから得られたという想定です.
import numpy as np
from matplotlib import pyplot as plt
x = np.arange(0, 10, 0.1)
y = np.exp(x)
plt.plot(x, y)
plt.show()
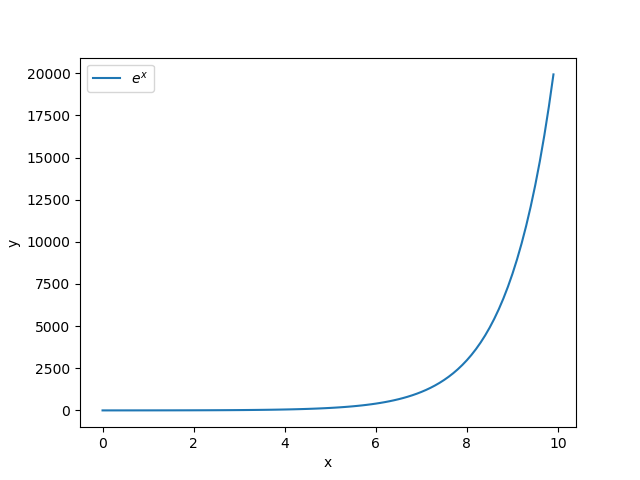
次に片対数グラフを描画します.
plt.yscale('log') # y軸を対数表示に
plt.plot(x, y)
plt.show()
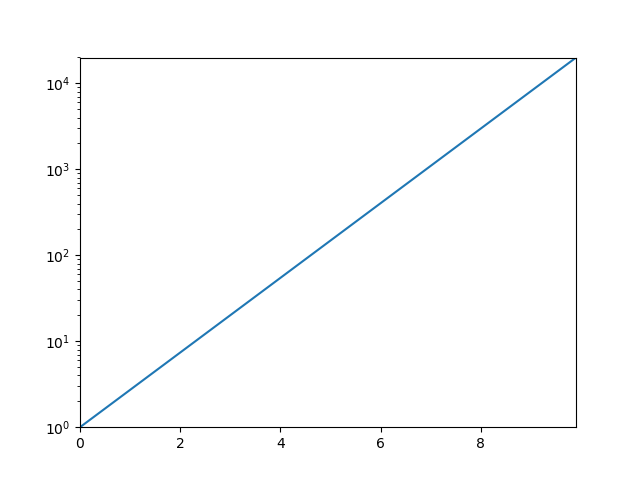
片対数グラフで描画すると直線になりました.
この直線の傾きと切片から,本来未知である$y=Ca^x$の$C$と$a$がわかります.
手順2 傾きと切片を求める
片対数グラフでは,y座標の間隔が調整されているだけで値は変わってません.そのため,このまま直線の傾きを求めようとしても,傾き一定に__見えている__だけなので増加率は場所によって異なってきます.
ではどうするかというと,グラフから読み取れる2つの座標$(x_1, y_1)$,$(x_2, y_2)$のうち,y座標に常用対数$\log_{10}$をとった上で傾き$a$を計算します.
\begin{equation}
a = \frac{\log_{10} y_1-\log_{10} y_2}{x_1-x_2} \\
\end{equation}
実際にグラフを読み,適当な二点を取り出してみます.
In [92]: x[10], np.log10(y[10])
Out[92]: (1.0, 0.4342944819032518)
In [93]: x[35], np.log10(y[35])
Out[93]: (3.5, 1.5200306866613813)
直線の式を$Y=ax+b\quad(Y=\log_{10} y)$とすれば,通る2点の座標から
$a=0.434...$
$b= 2.220\times 10^{-16}\cong0$
と求まります.
手順3 指数のべきと底を求める
直線の式を$(y=)$と書き直せば
\begin{eqnarray*}
\log_{10}y &=& ax+b \\
y &=& 10^{ax}10^{b} \\
&=& 10^{0.434x} \\
&=& (10^{0.434})^{x}
\end{eqnarray*}
$10^{0.434}=2.716...$なので,だいたい$e=2.718...$に近い値を求めることができました.