【TG WEB】直方体に穴をあける問題をPython, tkinterで解く

背景

最近、就活でWEBテストを受ける機会が増えてきました。
テストにはいくつか種類があるのですが、TG WEBというテストではパズル要素の強い問題がよく出題されるようです。そんな中、今回取り上げたいのは次のような問題です。

####Q:図のように、小立方体を64個積み重ねて大きな立方体を作る。図の黒い点から、その面に垂直に穴を突き通すと、穴のあいた小立方体の数は何個になるか？

※以下では小立方体＝ブロック、穴のあいた小立方体＝穴あきブロックと呼びます。

この問題は実際には手で解くものですが、プログラミング実装の良い題材だと思ったので、Pythonとtkinterを用いてこの問題を解いてくれるGUIアプリを作ってみることにしました。任意の穴のあけ方に対応することを目標とます。

目次

• 本問題の解き方
• 実装したコードの紹介

では、順番に見ていきます。

本問題の解き方

ある参考書によれば、直方体を４層に分けてそれぞれの層の穴の数を数えればよいとのことでしたが、なんだか手間に感じたので(というよりもその解法が思いつかなかった)、私は集合の考え方で解きます。

集合$A,B,C$の要素数を、各面から見たときの穴あきブロック(小立方体)数としたとき、直方体全体の穴あきブロック数はその和集合$n(A\cup B \cup C)$となります。

これを部分集合で表し直すと、

\begin{eqnarray}
n(A \cup B \cup C)
&=& n(A)+n(B)+n(C)-[n(A\cap B)+n(B\cap C)+n(C\cap A)]\\&&
+n(A\cap B \cap C)
\end{eqnarray}

となるので、右辺の各量を求めればよくなります。
手順としては、

1. 各面から見た穴あきブロック数を求める
2. 二つの面に共通する穴あきブロック数を求める
3. 三つの面に共通する穴あきブロック数を求める

この順番に考えていきます。

1. 各面から見た穴あきブロック数を求める

$n(A)+n(B)+n(C)$を求めます

今回考えているのは$4\times4\times4$のブロックで構成された直方体なので、A,B,Cの表面に見えている穴の数の合計を4倍すれば求まります。求めるブロック数を$N_1$とすれば、

N_1=(3+3+2)\times4=32

となります。

2. 二つの面に共通する穴あきブロック数を求める

AとB、BとC、CとAを比較して、共有している穴あきブロックの数$n(A\cap B)+n(B\cap C)+n(C\cap A)$を求めます。

展開図のように各面を並べて、重複数を検討します。

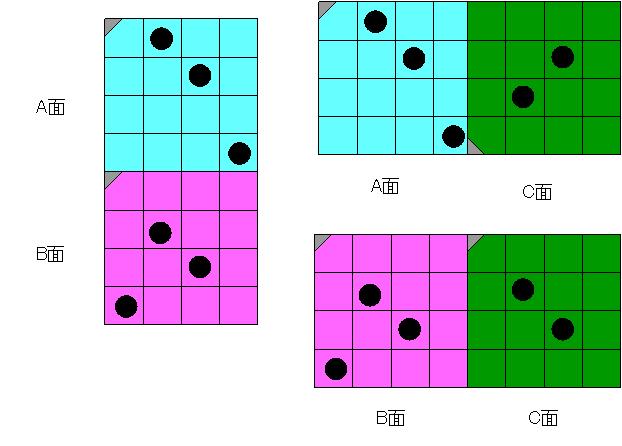
面を区別するために着色し、さらに面の基準を明らかにするために灰色の印をつけました。

この図から、例えばAとBでは縦の列について各面の穴の数を数えて積をとれば、二つの面に共通する穴あきブロックの数が求まります。具体的に計算すると以下のようになります。

\begin{eqnarray}
n_{AB}
&=& 0\times1+1\times1+1\times1+1\times0\\
&=& 2
\end{eqnarray}

4列すべての計算結果を足し合わせて完了です。同様の作業をBC,CAについても行います。こちらは横に比較します。

以上から求まる結果の和を$N_2$とします。

\begin{eqnarray}
N_2
&=& n_{AB}+n_{BC}+n_{CA}\\
&=& 2+2+1\\
&=& 5
\end{eqnarray}

3. 三つの面に共通する穴あきブロック数を求める

最後に、三面に共通する穴あきブロック$n(A\cap B \cap C)$について考えます。
素直に３つの集合に共通する要素数を数えれば良いでしょう。

全部で64個ある直方体のブロックを、それぞれ０から３の整数の組$(i,j,k)$で指定します。
$A_{ji}\cap B_{ki}\cap C_{kj}$が真となる組み合わせの数$N_3$を求めます。

この例題では

N_3=1

となり、最終的なこの問題の答えが出ます。

N_1-N_2+N_3=28

プログラミングによる実装

３つの面をそれぞれ4x4の配列で表し、チェックボタンを用いて条件を設定します。すると全体の穴あきブロック数が表示されます。

GUIの動作様子

例題と同じ条件に設定したところ、手計算で求まった28という結果が出ました。

実装したコードの解説

解説追記予定、コードだけ載せておきます。

import numpy as np
import tkinter as tk

class App(tk.Frame):
    def __init__(self, master=None):
        self.width = 4
        self.height = 4
        self.depth = 4
        tk.Frame.__init__(self, master)
        self.grid()
        self.setLabel()
        self.setCheck()
    
    def setCheck(self):
        self.buffer1 = [[tk.IntVar() for i in range(4)] for j in range(4)]
        self.buffer2 = [[tk.IntVar() for i in range(4)] for j in range(4)]
        self.buffer3 = [[tk.IntVar() for i in range(4)] for j in range(4)]

        for i in range(self.height):
            for j in range(self.width):
                self.buffer1[i][j].set(0)
                tk.Checkbutton(self, variable=self.buffer1[i][j], bg='cyan',\
                    command=self.count_through).grid(row=i, column=j)

        for i in range(self.height):
            for j in range(self.width):
                self.buffer2[i][j].set(0)
                tk.Checkbutton(self, variable=self.buffer2[i][j], bg='magenta',\
                    command=self.count_through).grid(row=i, column=j+self.width)

        for i in range(self.height):
            for j in range(self.width):
                self.buffer3[i][j].set(0)
                tk.Checkbutton(self, variable=self.buffer3[i][j], bg='green',\
                    command=self.count_through).grid(row=i, column=j+2*self.width)
    
    def setLabel(self):
        self.label = tk.Label(self, text='Result:\t'+'0')
        self.label.grid(row=4, column=0, columnspan=3)

    def count_through(self):
        nx = self.width
        ny = self.height
        nz = self.depth

        plane_A = np.empty((nx, ny))
        plane_B = np.empty((nx, nz))
        plane_C = np.empty((ny, nz))

        for i in range(4):
            for j in range(4):
                plane_A[i, j] = self.buffer1[i][j].get()
                plane_B[i, j] = self.buffer2[i][j].get()
                plane_C[i, j] = self.buffer3[i][j].get()


        #各行列の行ベクトルの要素の和を並べる
        vector_A = np.empty(ny)
        vector_B = np.empty(nz)
        vector_C = np.empty(nz)

        #各行列の列ベクトルの要素の和を並べる
        vector_tA = np.empty(nx)
        vector_tB = np.empty(nx)
        vector_tC = np.empty(ny)

        for i in range(nx):
            vector_tA[i] = plane_A[i, :].sum()
            vector_tC[i] = plane_C[i, :].sum()
        for j in range(ny):
            vector_A[j] = plane_A[:, j].sum()
            vector_tB[j] = plane_B[:, j].sum()
        for k in range(nz):
            vector_B[k] = plane_B[:, k].sum()
            vector_C[k] = plane_C[:, k].sum()

        #重複込の貫通数n1
        n1 = plane_A.sum() * nz + plane_B.sum() * ny + plane_C.sum() * nx

        #AB, BC, CAでの共通貫通ブロック数n2
        n2 = np.dot(vector_A, vector_B) + np.dot(vector_C, vector_tA) + np.dot(vector_tB, vector_tC)

        #ABC全てに共通する貫通ブロック数n3
        n3 = 0
        for i in range(nx):
            for j in range(ny):
                for k in range(nz):
                    #面Aと面Cではyの基準がずれているため、Cの補正をしている。
                    if plane_A[j, i] and plane_B[k, i] and plane_C[k, 3 - j]:
                        n3 += 1

        n = n1 - n2 + n3

        self.n1 = n1
        self.n2 = n2
        self.n3 = n3
        self.n = n
        self.plane_A = plane_A
        self.plane_B = plane_B
        self.plane_C = plane_C

        self.label.configure(text='Result:\t'+str(int(n)))

app = App()
app.mainloop()

今後の課題

• 任意のサイズの直方体で実行できるようにする
• 三面をリストとするときの基準位置の見直し
• コードのGUI部分と計算部分を独立させたい