ABC400 C - 2^a b^2
https://atcoder.jp/contests/abc400/tasks/abc400_c
ペナルティを出しつつなんとか解けました。復習のために記事にまとめました。
コンテスト中の自分の動き
順調に考察を進め、できたつもりで提出しましたが多くの人がやってしまったであろう sqrt の誤差の罠に引っかかってしまいました。
落ち着いて考え直して二分探索に方針変更し、正解できました。最初に二分探索をサボったのは悪手でした……。
以下の考察は僕がコンテスト中に考えた流れに沿って書きました。実際には頭が混乱していてここまで綺麗に考えられてはいませんし、図を描いたりする余裕もなかったのですが。
今後はコンテスト中に解くときにも一度落ち着いて図を描いてみるようにした方がいいかもしれませんね。
考察
良い整数の特徴
まずは入力例1を見ながら、良い整数を確認してみます。
\begin{align}
2 &= 2^1 ・ 1^2\\
4 &= 2^2 ・ 1^2\\
8 &= 2^3 ・ 1^2\\
16 &= 2^4 ・ 1^2\\
18 &= 2^1 ・ 3^2\\
\end{align}
16は $ 2^2 ・ 2^2 $ とも書けますが、右を $ 1^2 $ で揃えた方が統一感がありますね。ここで右を必ず奇数にできることに気づきます。実際、bが偶数の場合を考えて $b = 2c$ とすると $b^2 = 4c^2$ なので
\begin{align}
N &= 2^a ・ b^2 \\
&= 2^a ・ 4c^2\\
&= 2^{a+2} ・ c^2
\end{align}
とでき、a の方に$ b^2 $の偶数の部分が全て吸収されてしまいます。というわけで $ 2^a$ は言うまでもなく偶数、$ b^2 $は奇数なので両者を掛けた数字を数える際に重複を考える必要がなくなります。
良い整数を数える
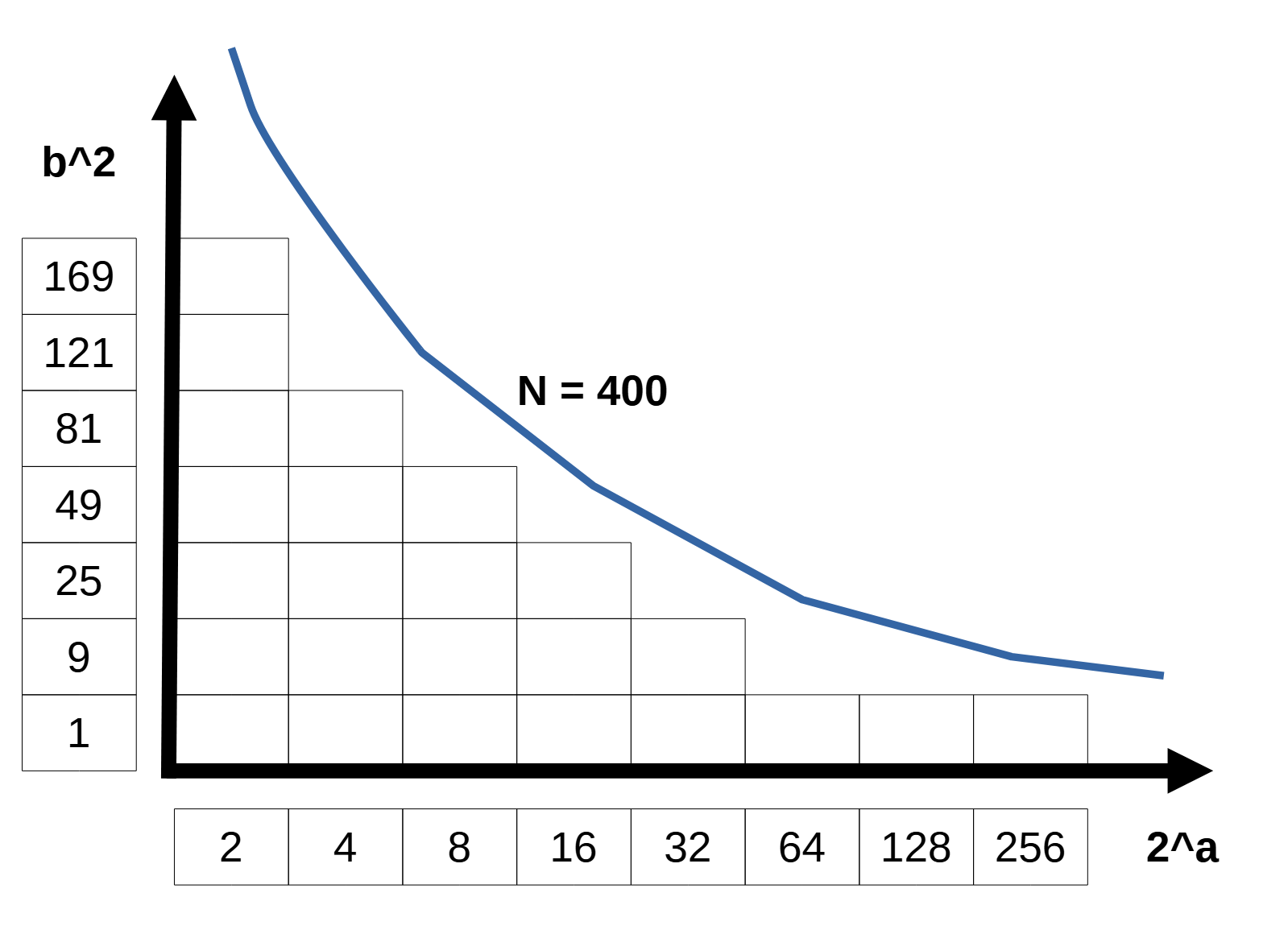
次に入力例2を見ながら考えます。N=400の場合、$ 2^a $と $b^2 $の関係はこのようになります。
条件を満たす整数(図中の長方形の数)を数えれば24個とわかります。定石通り変数の一方($ 2^a $, $ b^2 $ のどちらか)を固定し(全探索)、他方を工夫して探索することで計算量を抑えることを考えます。
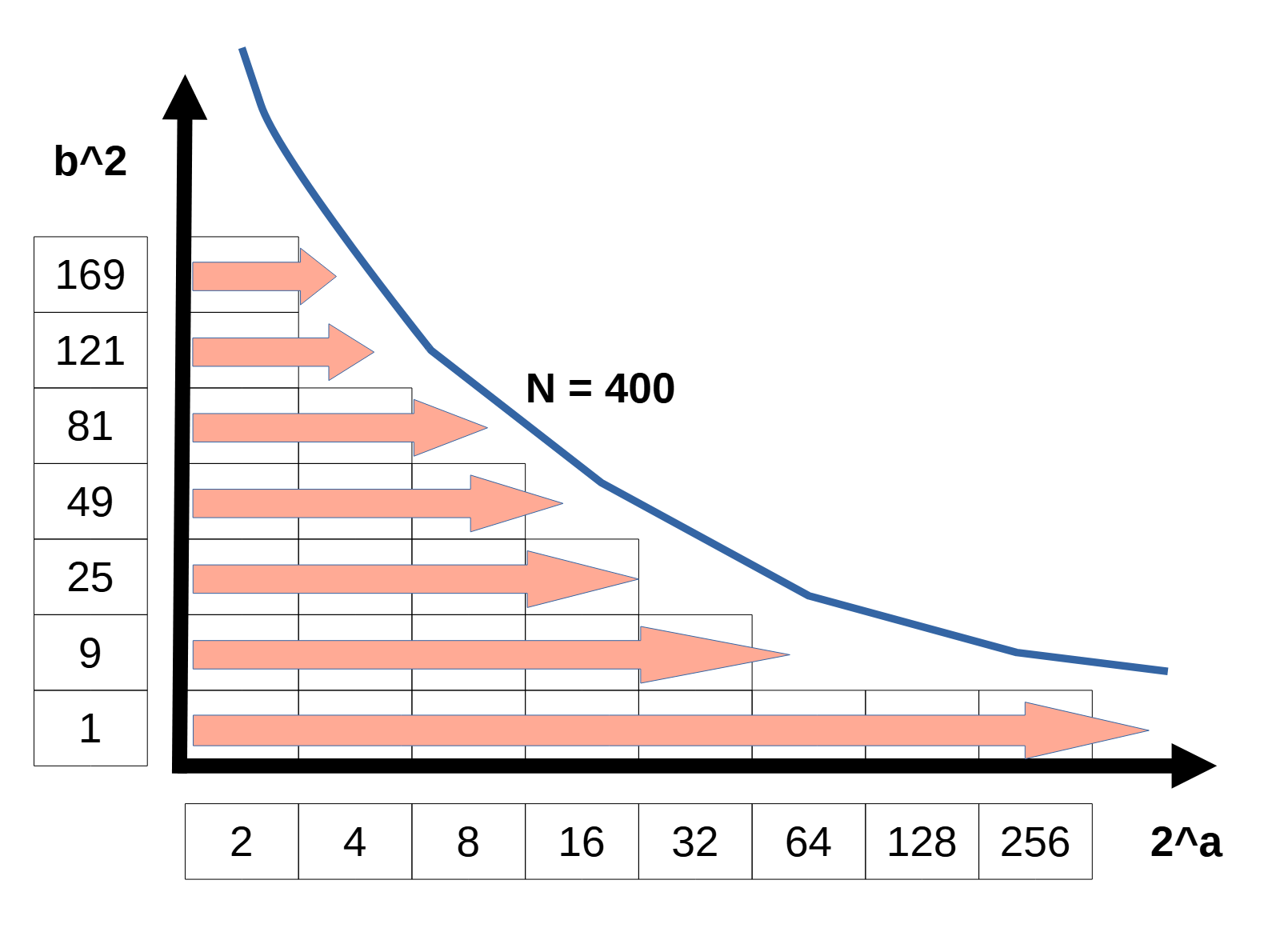
b を固定する調べ方
この図のように b ($ b^2 $) を全探索する場合を考えます。aは正整数なのでこうなります。
\begin{align}
2^a ・ b^2 &= N \leq 10^{18}\\
2 &\leq 2^a \leq \frac{10^{18}}{b^2}\\
b &\leq \sqrt{\frac{10^{18}}{2}} = \frac{10^9}{\sqrt{2}}
\end{align}
bの取りうる範囲が大きすぎますね。これを全探索するとTLEになってしまいます(公式のユーザ解説によればこれでもACできるようですが……)。
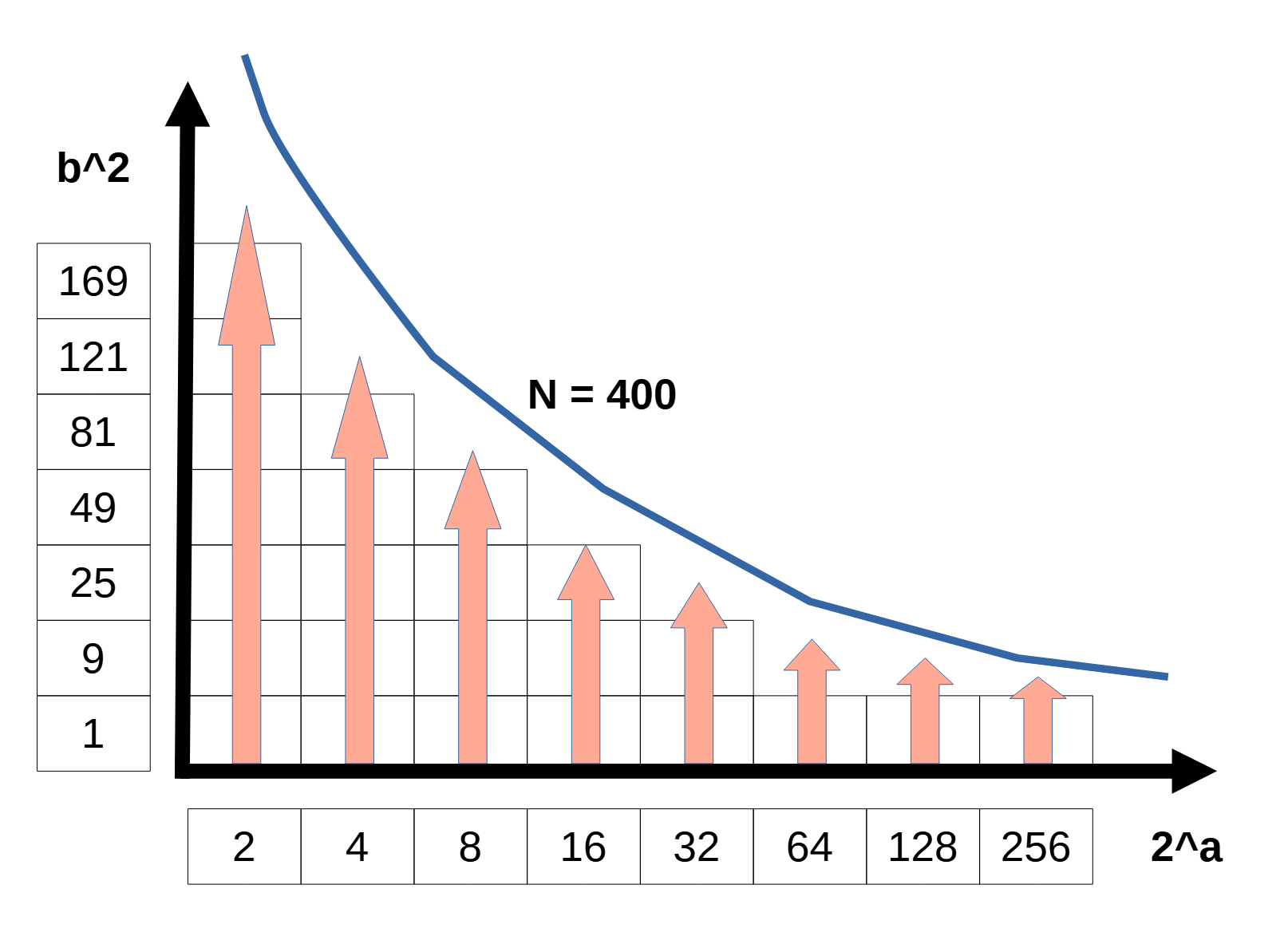
a を固定する調べ方
次にこの図のように a ($2^a$)を全探索する場合を考えます。b は正整数という条件から $ b^2 \geq 1$ なので、
\begin{align}
2^a ・ b^2 &= N \leq 10^{18}\\
1 &\leq b^2 \leq \frac{10^{18}}{2^a}\\
2^a &\leq 10^{18}
\end{align}
です。これなら全探索できますね。$ 2^{60} $ が $ 10^{18} $ より少し小さいぐらいなので念のため $ 2^1 \leq 2^a \leq 2^{70} $ の範囲で調べます。 (※修正。逆ですね。$ 2^{60} $ の方が $ 10^{18} $より少し大きいです。)というわけで $ 1 \leq a \leq 70 $ の範囲で (※これも70のままでも支障はありませんが、実際には60までで十分だと思います。) a を動かしながら
\begin{align}
b^2 &\leq \frac{10^{18}}{2^a}\\
b &\leq \sqrt{\frac{10^{18}}{2^a}}
\end{align}
を満たす整数 b の最大値を求めます。多くの人が引っかかってしまったように、ここで math.sqrt を使ってしまったので WA が 4 つ出てしまいました。ついでに言うとこの後に math.floor も使うようにしたら WA が1つ増えました。
これではいけないと思い、二分探索に方針を変更します。できる自信がなかったか、ok, ng 等の設定ができる気がしなかったのか……。今になって思うとこの考察のように図を描けば簡単にできた気もします。
実装
二分探索の最大値 ng の設定 $ 10^9 $ は勘で決めましたが、今思えば割と適切だった気もします。たぶんこの二分探索ならある程度以上大きければどう設定しても問題ないはず……。
def solve(arg, n, m):
# arg <= √(n/m) を両辺二乗して m を掛ける
return (arg ** 2) * m <= n
N = int(input())
ans = 0
for a in range(1, 71):
aa = pow(2, a) # √(N/aa) 以下の最大の整数を探す
ok = 0
ng = 10**9
while (abs(ok - ng) > 1):
mid = (ok + ng) // 2
if solve(mid, N, aa):
ok = mid
else:
ng = mid
b = (ok+1)//2 # ok 以下の最大の奇数
ans += b
print(ans)
逆に b の方に a を吸収させる考え方
2025/04/07 追記です。
公式のユーザ解説にあるエレガントな解法について後から読んで考えてみました。結局のところ、これはこの記事で書いた $ a $ に $ b^2$ の偶数の部分を全て吸収させる考え方とは逆で、$ b $ の方に$ 2^a $ の2乗の部分を全て吸収させる考え方ですね。コンテスト中にギリギリ思いつけなくもないかな?と思いました。
例えば a が偶数のとき a = 2c として、このようになります。
\begin{align}
N &= 2^a ・ b^2 \\
&= 2^{2c} ・ b^2\\
&= 2^c ・ 2^c ・ b^2\\
&= 2^0・(2^c ・ b)^2\\
\end{align}
実際には a は正整数という条件から $a \geq 2$, $c \geq 1$ なので、
$$N = 2^2・(2^{c-1}・b)^2$$
とするのが正確でしょうか。 aが奇数なら $ a = 2c-1 $ ($a \geq 1$, $c \geq 1$)として
\begin{align}
N &= 2^a ・ b^2 \\
&= 2^{2c-1} ・ b^2\\
&= 2^1・2^{c-1} ・ 2^{c-1} ・ b^2\\
&= 2^1・(2^{c-1} ・ b)^2\\
\end{align}
重複が気になるところですが、$ (2^{c-1}・b)^2 $ 部分で全ての平方数を表せるため、それぞれ
\begin{align}
N = 2・b^2 \\
N = 4・b^2
\end{align}
とできます。このとき $ b \geq 1$ なので重複はしません。