ABC404 E - Bowls and Beans
https://atcoder.jp/contests/abc404/tasks/abc404_e
コンテスト本番中に解けず、さらに解説を読んでもなお理解できなかったのですが、2日経ってようやく自分なりの解き方がわかりました。
コンテスト中の自分の動き
D問題までを30分で解き終え、E問題にたっぷりと時間を残すことができました。そして
- なるべく手前の($i$の小さい)茶碗に豆を運びたい。また、既に豆が入っている茶碗に豆を運んだ方が操作回数が少なく済むはず。
- 手前を優先すべきか、豆の入った茶碗を優先すべきか?
- 豆はなるべくまとめたいので、他の茶碗に入れる際に分ける意味はないはず。
などと考え、制約 N が小さいので DP で解けると予想しました。理解できた今になってから見直すと、ここまでわかっていてなぜ解けなかったのかと疑問に思ってしまいます。
コンテスト中は DP の配列や遷移がうまく作れませんでした。こんなことを考えていました。
- $ dp[i][j] := $ 茶碗 i に豆が j 個入った状態(i+1 以降は全て空)にするのに必要な操作回数の最小値
- $ dp[i] := $ 茶碗 i-1 までが初期値、茶碗 i に残りの豆全部、i+1 以降が空な状態にするまでの操作回数の最小値
豆の個数が 2000 以下になる制約に引っ張られて DP 配列に入れています。まとめて移せばいいので豆の個数は関係ないと気づいてからはそれを外してみたり。豆が入っている or 入っていないの 2 つの状態しかないのなら茶碗と豆の状態を $ 2^N $ で管理……も当然ダメですね。
そんなことを考えながら1時間以上が経過し、諦めました。
コンテスト後
いろんな解説を読みながら理解しようと考えていたときに「豆を飛び越す意味はない」という旨の記述を目にしました。確かに直感的にはそうなんですが、何故そうなるのか確信が持てませんでした。また、「貪欲で解ける」とも言われていましたが茶碗の遷移の際には $ C_i $ の大きな茶碗を狙って移動した方がいい場面もあるはずで、やっぱり DP ではないか?ということも考えていました。
そんなこんなで一旦は理解を諦めましたがやっぱり頭の中にはこの問題が残っており、翌日歩いているときに豆をまとめた方がいい理由をやっと思いつきました。
考察
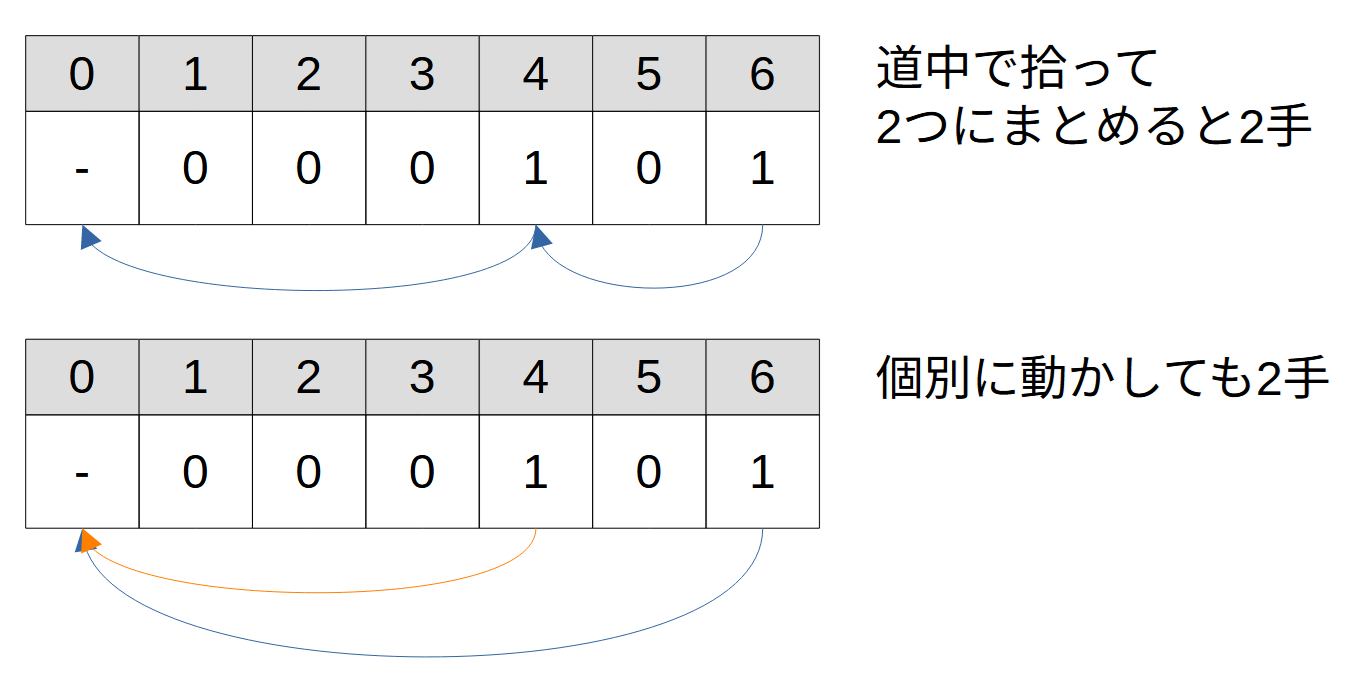
豆を同じ茶碗にまとめることで一緒に動かせるようになり、手数の節約になります。そして、一度まとめた後は最後まで一緒に動かすことができるので、まとめるならなるべく早い方がいいです。実際、最小の場合で考えてみると以下の画像のように、手数が同じになることはあっても余計に増えることはありません(増えてしまうパターンが思いつかない)。
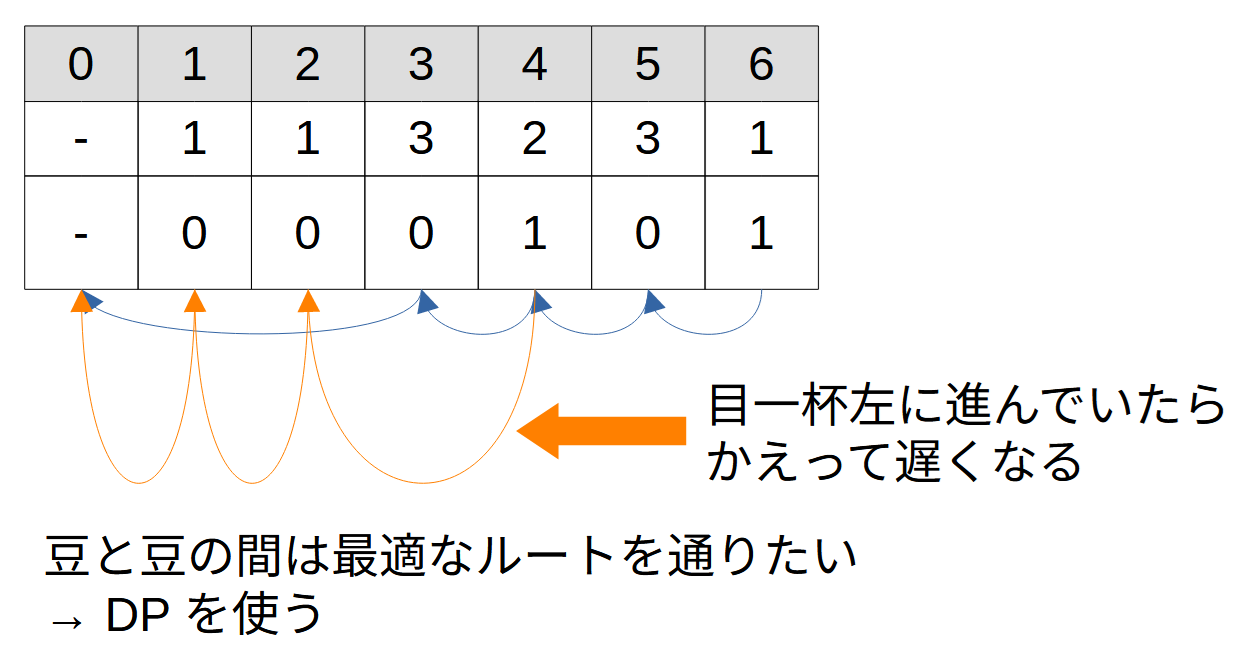
というわけで、豆のある茶碗から豆のある茶碗へと移動していく方針で考えていくことにします。その上でどう移動するかですが、例えば毎回目一杯 $C_i$ の分だけ進んでいくと余計に手数がかかってしまう場合があります。そこで、ようやく DP の出番です。よくある問題ですね。
1つ前の回、 ABC403-D でも部分的に DP を活用する考え方が出てきましたがそれと同じですね。反省点、敗因としては視野が狭かったことがいえます。制約から DP、貪欲では無理だから DP と決めつけてしまっていました。そして、いつもの DP のやり方に当てはめることしか考えていませんでした。貪欲だけでは無理、DPだけでも無理。「部分問題に分割してからの DP」という典型もあるということなのでしょう。ABC403-D のときは思いつけたのに今回は無理だったのは、いかにも DP で解けそうな見た目をしていたからだと思います。僕の場合 ABC403-D は考えていく途中で「ここで DP 使えそうじゃない?」と思いついたのでそこの違いでしょう。
実装
まず豆が置かれた茶碗の一覧 $beans$ を用意し、それを順番に辿っていきます。豆が置かれた茶碗 $now$ から次の豆が置かれた茶碗 $next$ までの移動に DP を使いますが、毎回 $ DP[直前の豆が置かれた茶碗] $ の値を利用できるので DP の配列は最初に 1 つ用意すれば十分です。
N = int(input())
C = [-1] + list(map(int, input().split()))
A = [-1] + list(map(int, input().split()))
beans = [0] # 豆が置かれた茶碗のリスト。終点として 0 も加える。
for i, a in enumerate(A):
if i == 0: continue
if a == 1:
beans.append(i)
beans.sort(reverse=True)
INF = 10**20
dp = [INF for _ in range(N)]
dp[beans[0]] = 0
for i in range(len(beans)-1):
# 茶碗[beans[i]] から 茶碗[beans[i+1]] に移動する。
now, next = beans[i], beans[i+1]
for j in range(now, next, -1):
for k in range(1, C[j]+1): # 1-C[j]まで全ての遷移パターンを調べる
if j - k > next: # next に到達できない場合は C[j] の分だけめいっぱい移動する
dp[j - k] = min(dp[j - k], dp[j] + 1)
else: # next 以下に到達できる場合は next で止まる
dp[next] = min(dp[next], dp[j] + 1)
print(dp[0])