はじめに
こんばんは,老技術者でございます。先日,新型コロナウィルスの特集番組を見ていたら抗体検査のところでIgMだのIgGだのって聞き覚えのあるワードが飛び込んできました。記憶を呼び起こしてみたら…はい,やってました。某検査屋さんからの案件で,電気泳動画像からの異常判定のプログラムを書いておりました。IgMだのIgGだのってのはそこに登場する免疫グロブリンのクラス名だったのです。
人の命にかかわることだから,偽陰性(本当は異常なのに陰性と判定してしまう)ってのはまずいですよね。でも疑わしきはじゃんじゃん陽性にすると,これから話題にする偽陽性(本当は正常なのに陽性と判定してしまう)が増えて検査の信頼性に関わるのでこれまた物言いがつきます。これを複数のパラメータのそれぞれの閾値を動かすことで良い案配にチューニングするのです。その微妙な匙加減を自動化するのが老技術者の腕の見せ所なのでした。
ところが,どう匙加減を調整してもなかなか陽性判定検体中の偽陽性の割合が減らないことがあります。それが,病理検査でありがちな「不均衡データ」(例えば,感染検体数が非感染検体数に比べて100分の1とか)の場合です。
そこで今宵のお話は,閾値の選び方によって,病理検査結果がこうも変わるんだ!ということを数値実験で体感するとともに「不均衡データ」の扱いの難しさについてもわかった感じになっていただこうと思います。なお,以下では話を分かりやすくするために,感染症の抗体検査を例に説明していきます。
仮定
次の単純な仮定を置いて考えることにします。
1. 陰性/陽性判定のための閾値を設定するパラメータは1つだけである
2. そのパラメータに対して,非感染(陰性)検体,感染(陽性)検体それぞれが正規分布している
この2つの仮定のもとに,まずは個体数,標準偏差が全く同じで平均だけが違う2つの群のデータを生成します(図1)。
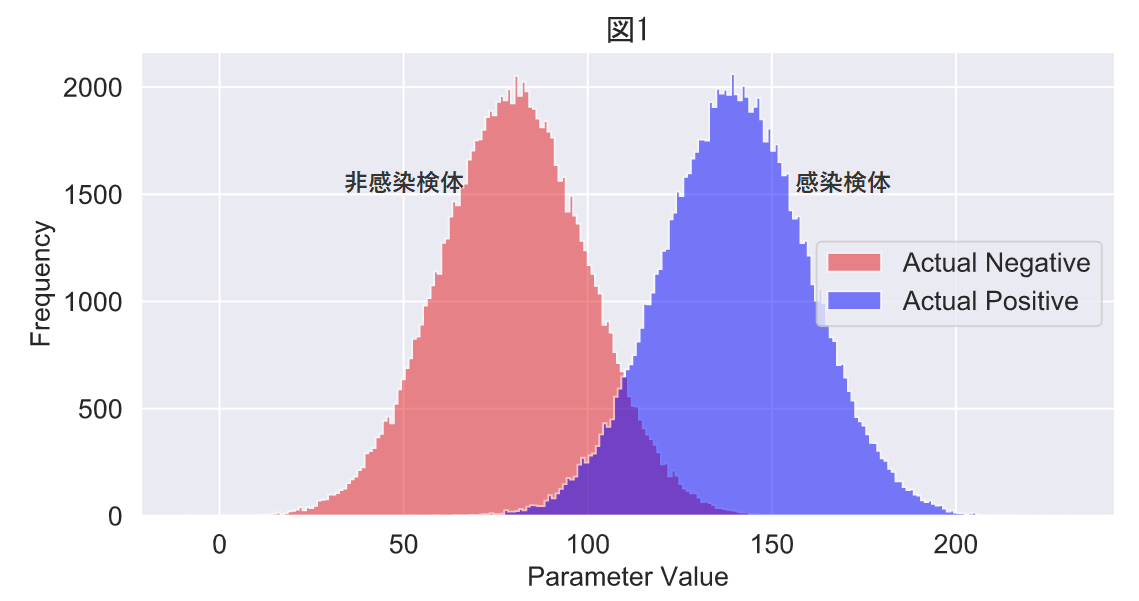
このヒストグラムで,左の赤い山が実際の非感染検体,右の青い山が実際の感染検体です。
用語の整理
はじめに図2を見ながら今回使用する用語の整理をしておきます。まず,パラメータ値の閾値(カットオフ値,Threshold)を決めます。青い線で示したのが閾値とするとその左側が陰性判定,右側が陽性判定となります。次に「実際に非感染検体か感染検体か」と「判定が陰性判定か陽性判定か」の組合せで次の4つのカテゴリーを定義します。
| 分類名 | 覚え方 | 定義 | ||
|---|---|---|---|---|
| TN | True Negative | 真陰性 | 正しく陰性 | 非感染検体を正しく陰性と判定 |
| FP | False Positive | 偽陽性 | 間違えて陽性 | 非感染検体を間違えて陽性と判定 |
| FN | False Negative | 偽陰性 | 間違えて陰性 | 感染検体を間違えて陰性と判定 |
| TP | True Positive | 真陽性 | 正しく陽性 | 感染検体を正しく陽性と判定 |
Tを「正しく」,Fを「間違えて」,Pを「陽性」,Nを「陰性」と読み替えると覚えやすいです。
いま仮に閾値(Threshold,青線)を100として,その左側が陰性判定(Negative),右側が陽性判定(Positive)であるとします。先ほどのヒストグラムに色を付けて,TN,FP,FN,TPの定義を確認しましょう。

非感染検体だけを見てみると,図3のようになります。
青線の左側は「正しく陰性判定」つまり真陰性(TN),
青線の右側は「間違えて陽性判定」つまり偽陽性(FP)
となります。

感染検体だけを見てみると,図4のようになります。
青線の左側は「間違えて陰性判定」つまり偽陰性(FN),
青線の右側は「正しく陽性判定」つまり真陽性(TP)
となります。

分類の評価
閾値を設定して,検体を陰性・陽性に分類する際,この分類の評価はどのようにしたらよいでしょうか?
まずは,先ほど紹介したTN,FP,FN,TPそれぞれの個体数を数えて表にします。この表のことを**混同行列(confusion matrix)**といいます。
| 予測 | |||
|---|---|---|---|
| 陰性 | 陽性 | ||
| 検体 | 非感染 | TN | FP |
| 感染 | FN | TP | |
閾値を決めるうえで注目するのは次の4つの指標です。
(1) 正解率(accuracy)
正解率は全個体の中で正しく予測できたものの割合で
$$
正解率=\frac{TN + TP}{FN + FP + TN + TP}
$$
と計算します。色分けしてこの定義式と混同行列との関係を見ると次のようになります。

(2) 適合率(precision)
適合率は陽性と判定した中で正しく予測できたものの割合で
$$
適合率=\frac{TP}{FP + TP}
$$
と計算します。色分けしてこの定義式と混同行列との関係を見ると次のようになります。

(3) 真陽性率(true positive rate,TPR)
再現率は感染検体の中で正しく陽性と予測できたものの割合です。
再現率(recall),感度(sensitivity)ともいい,
$$
真陽性率=\frac{TP}{FN + TP}
$$
と計算します。色分けしてこの定義式と混同行列との関係を見ると次のようになります。

(4) 偽陽性率(false positive rate,FPR)
偽陽性率は非感染検体の中で誤って陽性と予測してしまったものの割合で
$$
偽陽性率=\frac{FP}{TN + FP}
$$
と計算します。色分けしてこの定義式と混同行列との関係を見ると次のようになります。

例えば閾値が100の場合の混同行列は下表のようになります。
| 予測 | |||
|---|---|---|---|
| 陰性 | 陽性 | ||
| 検体 | 非感染 | 84006 | 15994 |
| 感染 | 2321 | 97679 | |


閾値が130の場合の混同行列は下表のようになります。
| 予測 | |||
|---|---|---|---|
| 陰性 | 陽性 | ||
| 検体 | 非感染 | 99388 | 612 |
| 感染 | 30766 | 69234 | |

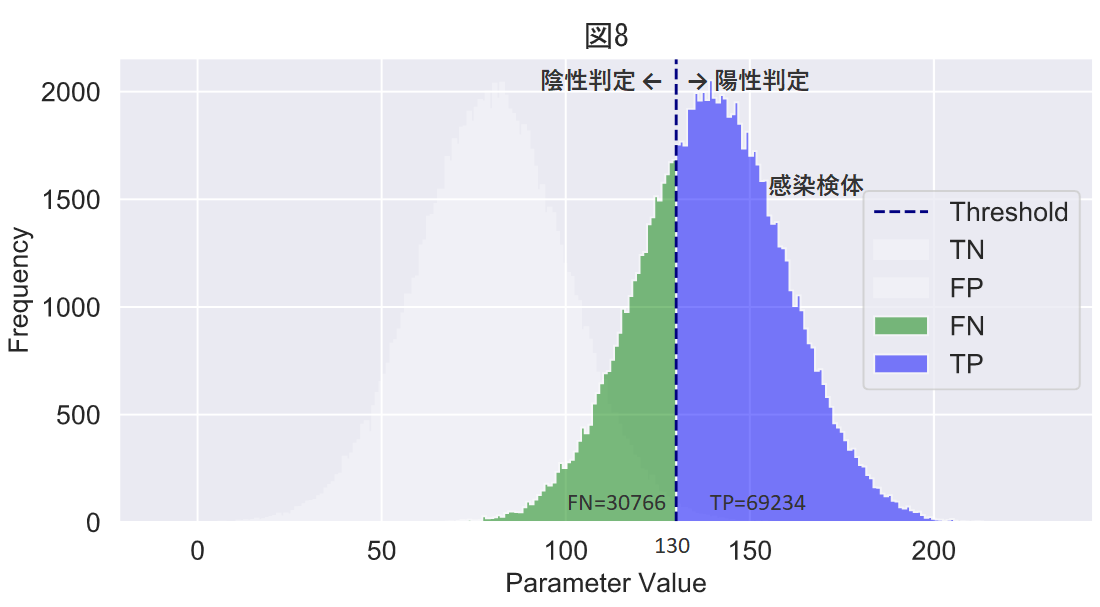
つまり閾値を100から130にすると
| 予測 | |||
|---|---|---|---|
| 陰性 | 陽性 | ||
| 検体 | 非感染 | TN 増 | FP 減 |
| 感染 | FN 増 | TP 減 | |
となることがわかります。上記の4つの評価指標を計算してみると下表のようになります。
| 評価指標 | 閾値 | |
|---|---|---|
| 100 | 130 | |
| $$ 正解率=\frac{TN + TP}{FN + FP + TN + TP} $$ | 0.90842 | 0.84311 |
| $$ 適合率=\frac{TP}{FP + TP} $$ | 0.85929 | 0.99123 |
| $$ 真陽性率=\frac{TP}{FN + TP}=再現率 $$ | 0.97679 | 0.69234 |
| $$ 偽陽性率=\frac{FP}{TN + FP} $$ | 0.15994 | 0.00612 |
閾値を連続的に変えていったときにこれらの評価指標がどう変化するかを図示すると図9のようになります。

閾値が100の場合と130の場合を比較してみると,病理検査で重要な真陽性率は閾値100の方が高く,それとトレードオフ関係になる適合率も0.85付近とそこそこ高くなっています。一方,閾値130では適合率はほぼ1になっていますが真陽性率が0.7未満ということで感染検体の30%以上を陰性と判定して見逃してしまうことになります。
そこで見逃しが許されない病理検査でしたら閾値100かさらにその下の閾値を使うのが良いということになります。
不均衡データの場合
上の数値実験は感染検体と非感染検体が同数というケースでした。しかし,実際の病理検査ではたいていの場合,非感染検体に比べ感染検体が著しく少ない,いわゆる不均衡データとなります。この場合,何が違ってくるでしょうか。いま10万:1万の不均衡データを生成してみました。

閾値が100の場合の混同行列は下表のようになります。
| 予測 | |||
|---|---|---|---|
| 陰性 | 陽性 | ||
| 検体 | 非感染 | 84006 | 15994 |
| 感染 | 657 | 9343 | |

となります。
非感染検体だけ取り出してみると

これは均衡データの場合と同じですので図5と全く同じになっています。
次に感染検体だけ取り出してみましょう。

となり,病理検査で問題となる偽陰性(FN)は小さく抑えられています。
ところが,検査の結果,陽性と判定された検体だけ見てみると,
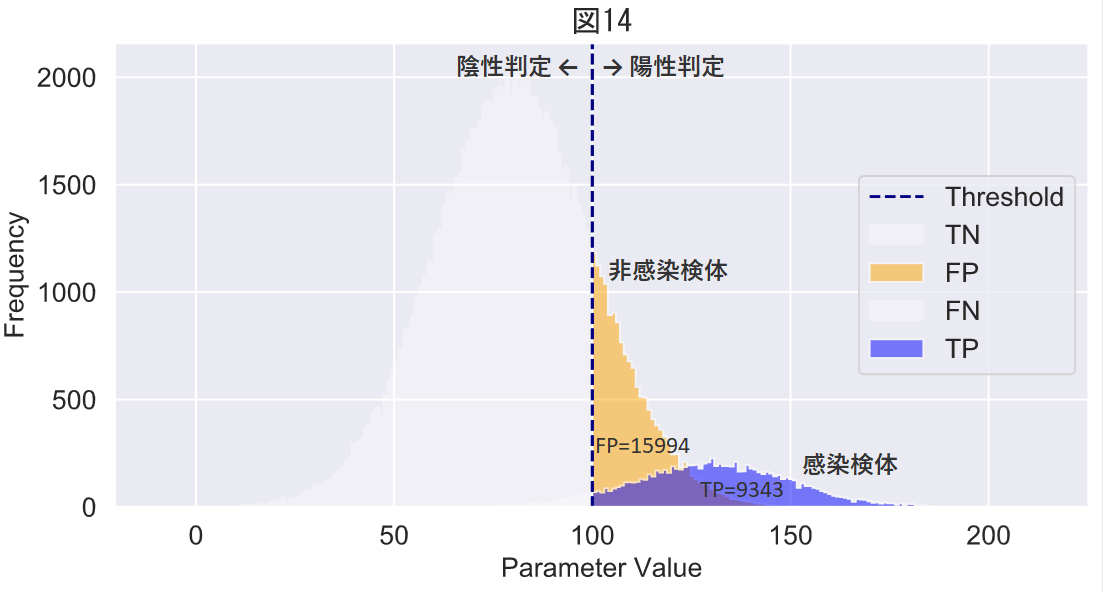
となります。適合率は陽性と判定した中で正しく予測できたものの割合で,閾値100では,
$$
適合率=\frac{TP}{FP + TP}=\frac{9343}{15994 + 9343}=0.3687
$$
となります。陽性と判定した検体中の偽陽性の割合(つまり1-適合率)が6割以上に達するというのは由々しき問題です。
閾値を上にずらしていけばこの偽陽性の割合は減っていきますが,代わりに本当は感染検体なのに間違って陰性と判定された検体(偽陰性)が増えてしまいます(図15)。これはもっと由々しい事態です。

つまり,不均衡データでは偽陰性検体数を抑えようとすると必然的に偽陽性検体数が著しく多くなってしまう,という一例が上の数値実験から示せたことになります。