データ解析ツールROOTでフィッティングしてみた

概要

前回、ROOTの基本的な説明を書きました。今回は実際に取ったデータをfittingします。コードはC++です。

データ

今回使うデータは電子の散乱角度です。霧箱を用いて測定しました。霧箱はかなりレガシーな検出器で、さまざまな放射線を検出するので、電子をその中から探す必要があります。この電子の判別については別記事を作ろうと思います。

データの可視化

まず取ったデータをグラフで表示します。ちなみにデータはcsv形式で、散乱角度のみのデータです。コードは以下の通りです。

graph.cpp

// this code is for draw histgram 


int graph(){
    gROOT ->Reset();

    FILE *fp;
    fp = fopen("data.csv","r");

    int tem;
    int i=0;
    double tem2;


    TH1S *h1 = new TH1S("Myhist","Scattering Angle",12,0,M_PI);


    while((fscanf(fp,"%d",&tem))!=EOF){
        tem2 = tem*M_PI/180;
        h1 -> Fill(tem2);
        i++;
    }    

    fclose(fp);

    gStyle -> SetOptFit();
    gStyle -> SetOptLogy();
    h1 -> Draw();
    h1 -> SetTitle("Scattering Angle");
    h1 -> GetXaxis()-> SetTitle("scattering angle [rad]");
    h1 -> GetYaxis()-> SetTitle("frequency");

    return 0;

}

前回通り、root graph.cppを実行すると

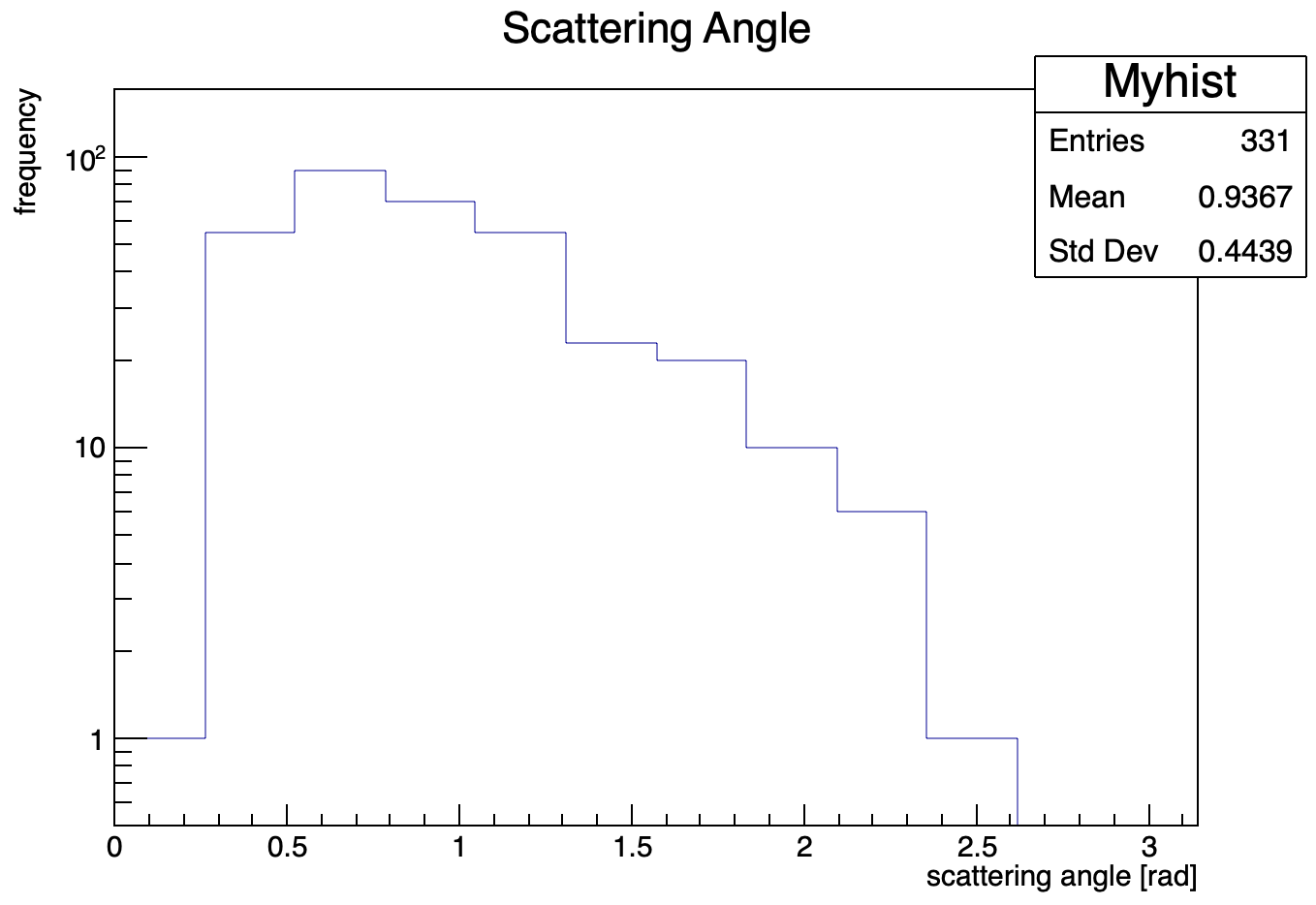
ちゃんと描画できました。
今回はイベント数が少ないのでヒストグラムで描画しています。binの幅は適当に15度としました。

ちなみに、C++なのにライブラリをincludeしてないのは、ROOTがインタプリタとして働いているからで、コンパイルがいらないのもこのためです。その代わりmain関数の名前はファイル名と一致させる必要があるので注意です。

fitting

この測定データを理論式でfittingします。理論式はsin関数の-4乗に比例します。比例係数はこの測定方法からもとまらないので、fiitingにより決定します。
まずはfittingし、描画するコードを示します。

fitting.cpp

// this code is for fitting


int fitting(){
    gROOT ->Reset();

    FILE *fp;
    fp =fopen("data.csv","r");

    int fitstart =40;
    int fitend =140;

    int tem;
    int i=0;
    double tem2;

    TH1S *h1 = new TH1S("Myhist","Scattering Angle",12,0,M_PI);
    TF1 *f = new TF1("f","[0]/sin(x/2)/sin(x/2)/sin(x/2)/sin(x/2)",1.,3.14);
    f ->SetParameter(0,3);


    while((fscanf(fp,"%d",&tem))!=EOF){
        tem2 = tem*M_PI/180;
        h1 -> Fill(tem2);
        i++;
    }    

    fclose(fp);

    gStyle ->SetOptFit();
    gStyle -> SetOptLogy();
    h1 ->Fit("f","","",fitstart*M_PI/180,fitend*M_PI/180);
    h1 -> Draw();
    h1 -> SetTitle("Scattering Angle");
    h1 -> GetXaxis()-> SetTitle("scattering angle [rad]");
    h1 -> GetYaxis()-> SetTitle("frequency");

    return 0;

}

実行すると、

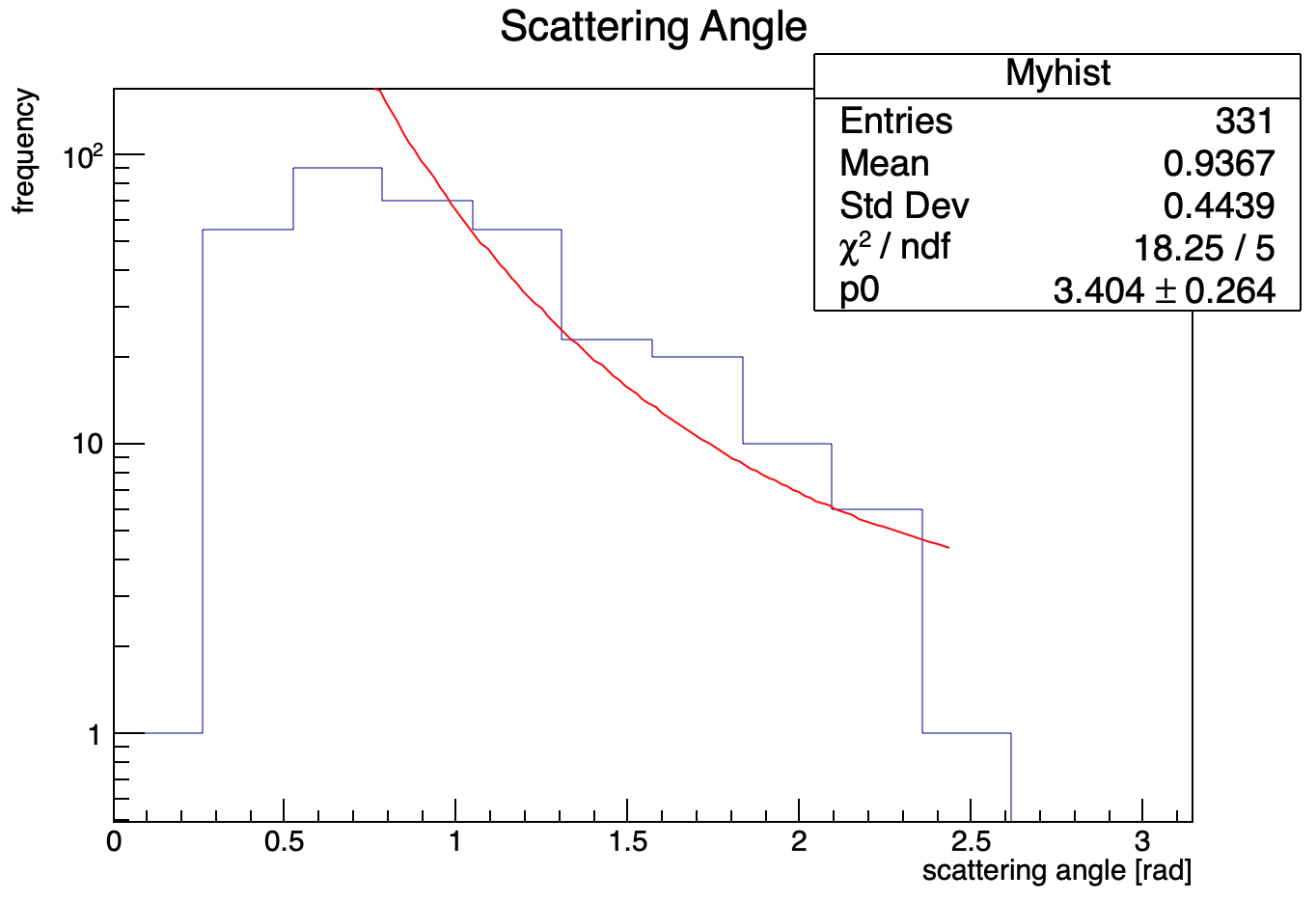
40~140度の区間でsin^-4でfittingできています。

fitting部分の解説

TF1 *f = new TF1("f","[0]/sin(x/2)/sin(x/2)/sin(x/2)/sin(x/2)",1.,3.14);

fというTF1クラスのインスタンスを生成しています。TF1は1変数関数のクラスです。第二引数で関数を定義しています。[0]の部分はfitting用のパラメタです。もしfiiting用のパラメタが複数ある場合は[1],[2]と中の数字を増やして使えば大丈夫です。第三、四引数は定義域を表しています。

h1 ->Fit("f","","",fitstart*M_PI/180,fitend*M_PI/180);

こうすると第一引数の関数でh1の関数をfittingしてくれます。fittingの範囲は第四、五引数の範囲です。このように範囲を指定するとfitting関数の定義域は無視でき、綺麗にfittingができます。第二、三引数は謎です。


今回は自分で定義した関数でfittingしてますが、ROOTが用意している関数でfittingすることもできます。例えばgauss関数でfittingしたい場合は

h1 ->Fit("gauss");

のようにシンプルに記述できます。


fittingを済ませた後はh1をDrawすればfitting関数も一緒に出てきます。

補足

実際に僕が描画しグラフには上の方にエントリ数や平均値などが出ている箱があります。それは統計BOXといって、使ったデータの数やカイ２乗、換算カイ２乗を計算して乗っけてくれる優れものです。コード内の

gStyle ->SetOptFit();

で表示を命令しています。

また、対数スケールで描画しているのは

gStyle -> SetOptLogy();

の部分が作用しています。

終わりに

こんな感じでめんどくさいfittingを数行で行うことができて、非常ありがたいツールという実感が湧きます。