[Unity] パスに沿った円柱(Cylinder)状のメッシュ生成

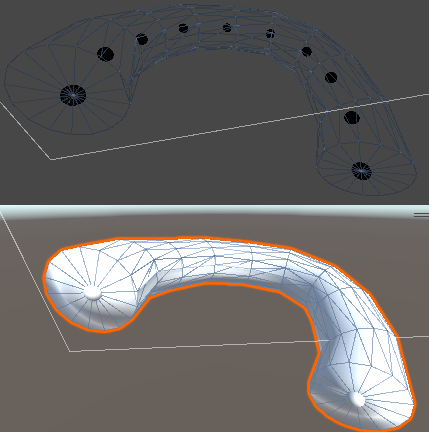
パスに沿った頂点の作り方はリンク先で解説しているので、本記事は円の頂点とトライアングルについての解説となります。

円の頂点座標の求め方

チューブ状のメッシュを生成するには高校の時に習った三角関数を思い出す必要があります。

図の例は８分割で円を作る場合で頂点の角度が360/8=45度です。
三角関数の公式に当てはめることで円の頂点座標を求めます。
コードにすると以下のようになります。

            int Division = 8;
            // 円の角度を分割数で割る
            float angleStep = (Mathf.PI * 2.0f) / Division;

            // 円周の頂点：反時計回り
            for (int j = 0; j < Division; j++)
            {
                float angle = j * angleStep;
                // 三角関数：sin(angle) = y, cos(angle) = x
                Vector3 vertic = positions[i] + rot * new Vector3(Mathf.Cos(angle), Mathf.Sin(angle), 0f) * Width;
                vertices.Add(vertic);
            }

円のトライアングルの生成

円の状のトライアングルを作る場合、円の中心の頂点を中心に外側の２点と結びます。
[1, 3, 2] [1, 4, 3] [1, 5, 4] [1, 6, 5] [1, 2, 6]
コードで書くと以下のようになります。

                // 表面用の円の中心点の配列番号
                int index = 0;

                for (int j = 0; j < Division; j++)
                {
                    triangles.Add(index);

                    if (j != Division - 1)
                    {
                        triangles.Add(index + j + 2);
                    }
                    else
                    {
                        triangles.Add(index + 1);
                    }

                    triangles.Add(index + j + 1);
                }
            }

全体のコード

表面と裏面を作るため、配列の最初と最後にそれぞれ面を作るための円の中心の頂点を格納しています。
トライアングルの計算で円周のトライアングルはその配列番号をオフセットした計算になっています。

GeneratePathCylinder.cs

using System.Collections.Generic;
using UnityEngine;

public class GeneratePathCylinder : MonoBehaviour
{
    class Square
    {
        public Vector3 lowerLeft;
        public Vector3 upperLeft;
        public Vector3 lowerRight;
        public Vector3 upperRight;
    }

    [SerializeField] Transform[] PathPosition;
    [SerializeField] Material Material;
    [SerializeField] float Width = 1f;
    [SerializeField] int Division = 16;
    [SerializeField] bool IsDrawGizmo = false;



    // Start is called before the first frame update
    void Start()
    {
        GenerateMesh();
    }

    private List<Vector3> CreateVertices()
    {
        int length = PathPosition.Length;
        var positions = new Vector3[length];
        var vertices = new List<Vector3>();

        for ( int i = 0; i < length; i++)
        {
            positions[i] = PathPosition[i].position;
        }

        for (int i = 0; i < positions.Length; i++)
        {
            Vector3 firstPos, secondPos;

            if (i == 0)
            {
                firstPos = positions[0];
                secondPos = positions[1];
            }
            else
            {
                firstPos = positions[i - 1];
                secondPos = positions[i];
            }

            Vector3 direction = (secondPos - firstPos).normalized;
            Quaternion rot = Quaternion.LookRotation(direction);

            // 円の角度を分割数で割る
            float angleStep = (Mathf.PI * 2.0f) / Division;

            // 表面用の円の中心点
            if (i == 0)
            {
                vertices.Add(positions[i]);
            }

            // 円周の頂点：反時計回り
            for (int j = 0; j < Division; j++)
            {
                float angle = j * angleStep;
                // 三角関数：sin(angle) = y, cos(angle) = x
                Vector3 vertic = positions[i] + rot * new Vector3(Mathf.Cos(angle), Mathf.Sin(angle), 0f) * Width;
                vertices.Add(vertic);
            }

            // 裏面用の円の中心点
            if (i == positions.Length - 1)
            {
                vertices.Add(positions[i]);
            }
        }

        return vertices;
    }

    public void GenerateMesh()
    {
        var mesh = new Mesh();

        var vertices = CreateVertices();
        var triangles = new List<int>();

        int length = PathPosition.Length;

        for (int i = 0; i < length; i++)
        {
            if (i == 0)
            {
                // 表面用の円の中心点の配列番号
                int index = 0;

                for (int j = 0; j < Division; j++)
                {
                    triangles.Add(index);

                    if (j != Division - 1)
                    {
                        triangles.Add(index + j + 2);
                    }
                    else
                    {
                        triangles.Add(index + 1);
                    }

                    triangles.Add(index + j + 1);
                }
            }
            else
            {
                // 円周の面
                for (int j = 0; j < Division; j++)
                {
                    int lastIndex = (i - 1) * Division + 1;
                    int currentIndex = i * Division + 1;

                    int lowerLeft, lowerRight, upperLeft, upperRight;

                    if (j != Division - 1)
                    {
                        lowerLeft = lastIndex + j;
                        lowerRight = lastIndex + j + 1;
                        upperLeft = currentIndex + j;
                        upperRight = currentIndex + j + 1;
                    }
                    else
                    {
                        lowerLeft = lastIndex + j;
                        lowerRight = lastIndex + 1;
                        upperLeft = currentIndex + j;
                        upperRight = currentIndex + 1;
                    }

                    //triangles.AddRange(SquareToTriangles(lowerLeft, lowerRight, upperLeft, upperRight));
                    triangles.AddRange(SquareToTriangles(lowerRight, lowerLeft, upperRight, upperLeft));
                }

                if (i == length - 1)
                {
                    int index = i * Division + 1;
                    // 裏面用の円の中心点の配列番号
                    int index2 = Division * length + 1;

                    for (int j = 0; j < Division; j++)
                    {
                        triangles.Add(index2);
                        triangles.Add(index + j);

                        if (j != Division - 1)
                        {
                            triangles.Add(index + j + 1);
                        }
                        else
                        {
                            triangles.Add(index);
                        }
                    }
                }
            }
        }

        mesh.SetVertices(vertices);
        mesh.SetTriangles(triangles, 0);
        mesh.RecalculateNormals();

        var obj = new GameObject();
        obj.name = "GenerateMesh";
        obj.transform.parent = transform;
        var meshFilter = obj.AddComponent<MeshFilter>();
        var meshRenderer = obj.AddComponent<MeshRenderer>();
        var meshCollider = obj.AddComponent<MeshCollider>();

        meshFilter.mesh = mesh;
        meshCollider.sharedMesh = mesh;
        meshRenderer.material = Material;
    }

    private List<int> SquareToTriangles(int lowerLeft, int lowerRight, int upperLeft, int upperRight)
    {
        var triangles = new List<int>();

        triangles.Add(lowerLeft);   // 0
        triangles.Add(upperLeft);   // 2
        triangles.Add(lowerRight);  // 1

        triangles.Add(upperLeft);   // 2
        triangles.Add(upperRight);  // 3
        triangles.Add(lowerRight);  // 1

        return triangles;
    }

    private void OnDrawGizmos()
    {
        if((PathPosition == null) || (PathPosition.Length < 2) || !IsDrawGizmo)
        {
            return;
        }

        var vertices = CreateVertices();

        for (int i = 0; i < vertices.Count; i++)
        {
            Gizmos.DrawSphere(vertices[i], 0.1f);
        }
    }
}