1. はじめに
前回に引き続きPyTorchを用いたarXiv実装の2回目になります。今回紹介する論文はVISUALIZING THE LOSS LANDSCAPE OF NEURAL NETSになります。
扱う内容は前回と同じニューラルネットの可視化です。ただし前回は中間層の可視化でしたが、今回は出力層の可視化です。本論文ではディープラーニングのロス関数を可視化する手法を提案しています。
ディープラーニングの学習においては、SGDやAdaGradなどのアルゴリズムを用いてロス関数を最小とするパラメータの探索を行います。凸関数は局所最適化を繰り返すことで大域的最適解が得られますが、非凸関数ではその保障はありません(参照ページ)。そしてディープラーニングのロス関数は一般に凸関数とは限らないため、学習により適切なパラメータが求まる保障はありません。
しかし、適切なバッチサイズ・フィルタサイズを用いることやResNetのようにショートカットコネクションを用いることで学習が上手くいくケースが知られています。本論文ではなぜこれらのケースでは学習が上手く進むのかをロス関数の可視化という観点で検証しています。
2. 既存のロス関数の可視化手法
ディープラーニングのパラメータ数は多く、例えばAlexNetのパラメータ数は6000万個になります。そのためロス関数は高次元となります。そのためロス関数の可視化に関してはいくつかの手法が提案されていますが、どの手法でも共通するのは可視化において何らかの方法で次元を落とすことです。
2-1. 1-Dimensional Linear Interpolation
本手法はQualitatively characterizing neural network optimization problemsにて提案された手法です。学習開始時のパラメータを$\theta_i$を始点とし、学習完了後のパラメータ$\theta_f$を終点とます。$\alpha=0$が開始始点であり、$\alpha=1$が学習完了地点となるような$\theta_\alpha$を考えます。そしてロス関数を$\alpha$の関数$f(\alpha)$として扱います。
\theta_\alpha = (1 - \alpha)\theta_i + \alpha\theta_f
f(\alpha) = L (\theta_\alpha)
この手法は1次元線形補完という名前の通り、始点と終点のパラメータの内分点をロス関数の入力とします。つまり始点から終点方向に対して直線的に動かした場合のロス関数の値を可視化しています。当然ですが実際に学習の際のパラメータの経路がこの直線上という保障はありません。
本手法の実行結果例を以下に記載します。横軸$\alpha=0$が開始始点であり$\alpha=1$を学習完了地点とする1つのパラメータを持つ関数として、ロス関数が表現されています。

2-2. 2D Contour Plots
上記手法を拡張した手法です。適当な開始地点$\theta^*$に対して、2つのベクトル$\delta$および$\eta$を考えます。ここで$\delta$および$\eta$の方向はガウス分布を用いてランダムに生成します。そして$\delta$および$\eta$の張る平面上のパラメータをロス関数の入力とします。
f(\alpha, \beta) = L (\theta^* + \alpha\delta + \beta\eta)
本手法の実行結果例を以下に記載します。ロス関数が2つの独立のパラメータを用いて表現されています。

3. 新規に提案されたロス関数の可視化手法
3-1. 既存手法の問題点
2-2で紹介した方向ベクトル$\delta$および$\eta$をランダムとするアプローチはシンプルではありますが、ロス関数に固有の幾何学的性質を捉えるのに失敗する恐れがあります。
例として下のように畳み込み層(CNN)・バッチ正規化(BN)・活性化関数(ReLU)からなるシンプルな2つのモデルAおよびBを考えます。ここでモデルBのCNNの各パラメータの値を一律モデルAの10倍します。
モデルBではCNNの出力はモデルAの10倍になりますが、後続のBNにおいてミニバッチ毎の入力データを平均が0、分散が1のデータとなるように変換されます。つまりモデルAとモデルBはCNNの値が10倍されているにも関わらず、入力が同じならBNにより出力は同じです。
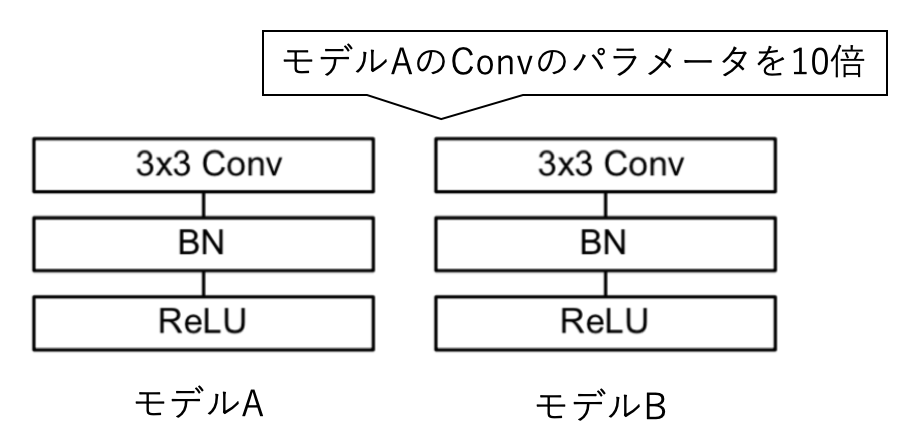
ここでモデルAおよびBのCNNの各パラメータの値を一律に0.1だけ増加させることを考えます。この場合母体のCNNのパラメータが違うので、モデルAのほうがモデルBよりも大きな影響を受けます。もしモデルAおよびBの影響を同じにするには、モデルBでは0.1ではなくその10倍の1だけ増加させる必要があります。

つまりモデルのパラメータの値を変更させる場合は、変更先となる母体のパラメータの値の大きさを考慮する必要があります。既存手法ではその考慮がありません。
3-2. FILTER-WISE NORMALIZATION
提案手法ではパラメータの値の更新時に、母体のフィルタの大きさに応じた正規化を行います。
今$i$番目のフィルタに加算される値を$d_i$とすると、各$d_i$に対して以下のように母体のパラメータ$\theta_i$の大きさに応じた正規化を行います。
d_i \leftarrow \frac{d_i}{||d_i||} ||\theta_i||
Pythonのコードの実装は以下の通りです。
def normalize_direction(direction, weights, norm='filter'):
if norm == 'filter':
# Rescale the filters (weights in group) in 'direction' so that each
# filter has the same norm as its corresponding filter in 'weights'.
for d, w in zip(direction, weights):
d.mul_(w.norm()/(d.norm() + 1e-10))
まとめると本論文では以下の手法でモデルの可視化を行います。
-
原点を学習済みのパラメータとし、原点を中心にして2つランダムな方向ベクトルの張る平面上のパラメータをロス関数の入力対象とする。
-
ロス関数の値を求める際は、Filter-Wise Normalizationを用いて正規化する。
3-3.ソースコード
本論文のソースコードはこちらに公開されています。私は勉強を兼ねて上記の本家版のソースコードを参考にこちらに簡易版を作成しました。
本家版は細かいパラメータや並列処理も可能ですが、簡易版では可視化対象のモデル以外は全て固定とし必要な最小限の処理のみを実装しています。処理の概要を追うだけなら簡易版のほうが容易です。
簡易版の実行方法は以下の通りです。なぜかGoogleColabだと失敗することがあります1。まずmain.pyでロスの計算を行い、その結果を3d_surface_file.h5に保存します。その後visualize.pyにて可視化を行います。
$ python -m src.main
$ python -m src.visualize
visualize.pyはGPUは不要ですがGUI環境が必要です。そのためmain.pyをGPUに対応したクラウド上で計算し、その後3d_surface_file.h5をローカルにコピーしてからvisualize.pyをローカル上で行うことを勧めます。
3-3-1. main.pyの概要
実行完了までにGoogleColab上でおよそ6時間程度はかかります。
# main.pyの概要
# 可視化対象モデルの作成
model = ResNet56_noshort()
# ランダムなベクトルの作成
rand_directions = create_random_directions(model)
# 可視化対象モデルの学習
# 学習結果はtrained_modelに保存
trained_model = prepare_trained_model(model)
# 最小値を中心としてランダムなベクトルの範囲内のロスを計算
# 最終的な計算結果は3d_surface_file.h5に保存される
calulate_loss_landscape(trained_model, rand_directions)
3-3-2. visualize.pyの概要
visualize.pyは3d_surface_file.h5を元にロス関数の3D表示・等高線表示・ヒートマップ表示を行います。以下にいくつか実行結果を記載します。
図の中心は学習完了時のパラメータを元に計算したロスの値です。そのため中心の原点がロスの値の最小値になります。縦軸および横軸は2つのベクトルの係数$\alpha$および$\beta$に対応します。
-
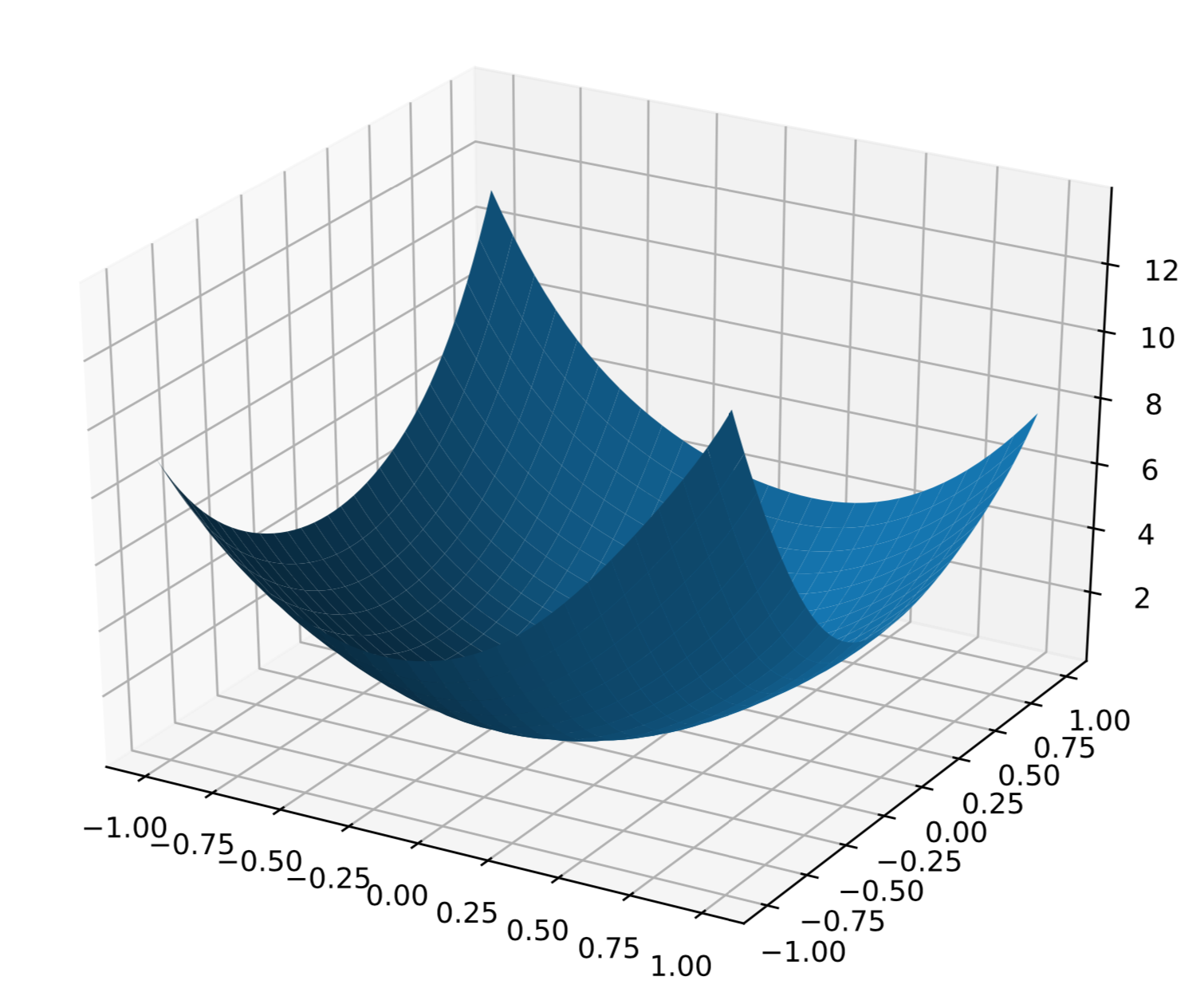
AlexNetの3D表示版:
綺麗な凸関数になっているのがわかります。
-
ResNet56(ショートカット無し)の3D表示版:
AlexNetと異なりショートカットの無いResNet56は学習が困難です。ロスが発散するためロスの上限を10に絞っていますが、明らかにAlexNetとは原点周辺とはロス関数の形状が異なります。

-
ResNet18(ショートカット無し)の等高線表示版
等高線表示版では、等高線に垂直な方向が原点を向いていれば学習が1直線に進むことを意味します。つまり等高線が同心円状ならばそれだけ学習は一本道なので容易となります。さらに等高線の間隔が密なほどロスの値の変化が激しいことを意味します。

-
ResNet18(ショートカット無し)のヒートマップ表示版
色が紺色に近いほどロス小さいことを意味します。原点周辺以外にも紺色の分布があることからロス関数が凸関数になっていないことがわかります。

4. 提案手法の検証
ここでは論文から上述の提案手法をResNetに適用した結果をいくつか抜粋します。論文の原文にはここで紹介したResNet以外の比較結果や、学習のトラジェクトリーの可視化手法の記載があります。
4-1. ネットワークの深さの影響の可視化
ResNet(ショートカット無し版)を可視化したのが下図です。ResNet20・ResNet56・ResNet101の3種類の可視化結果を比較しています。
ResNet20では同心円状の等高線が見られ凸関数となっていることがわかります。さらに等高線に垂直な方向がロスの最小値を向いていることが見て取れます。
ResNet56およびResNet101では等高線の分布は同心円でなくなり等高線の垂直な方向がロスの最小値とは不一致となっています。また等高線の間隔が密なことから値が急激に変化することが見て取れます。
これらからネットワークを深くするほど学習が困難になることが見て取れます。

4-2. ショートカットによる影響の可視化
ResNet20・ResNet56・ResNet101の3種類に対して、ショートカットあり版(上)となし版(下)の可視化結果を比較したのが下の図です。
ショートカットあり版(上)では等高線が同心円状に分布し間隔が疎になっています。ショートカットを加えることによりロス関数が凸関数となり、ネットワークを深くしても学習が可能なことが見て取れます。
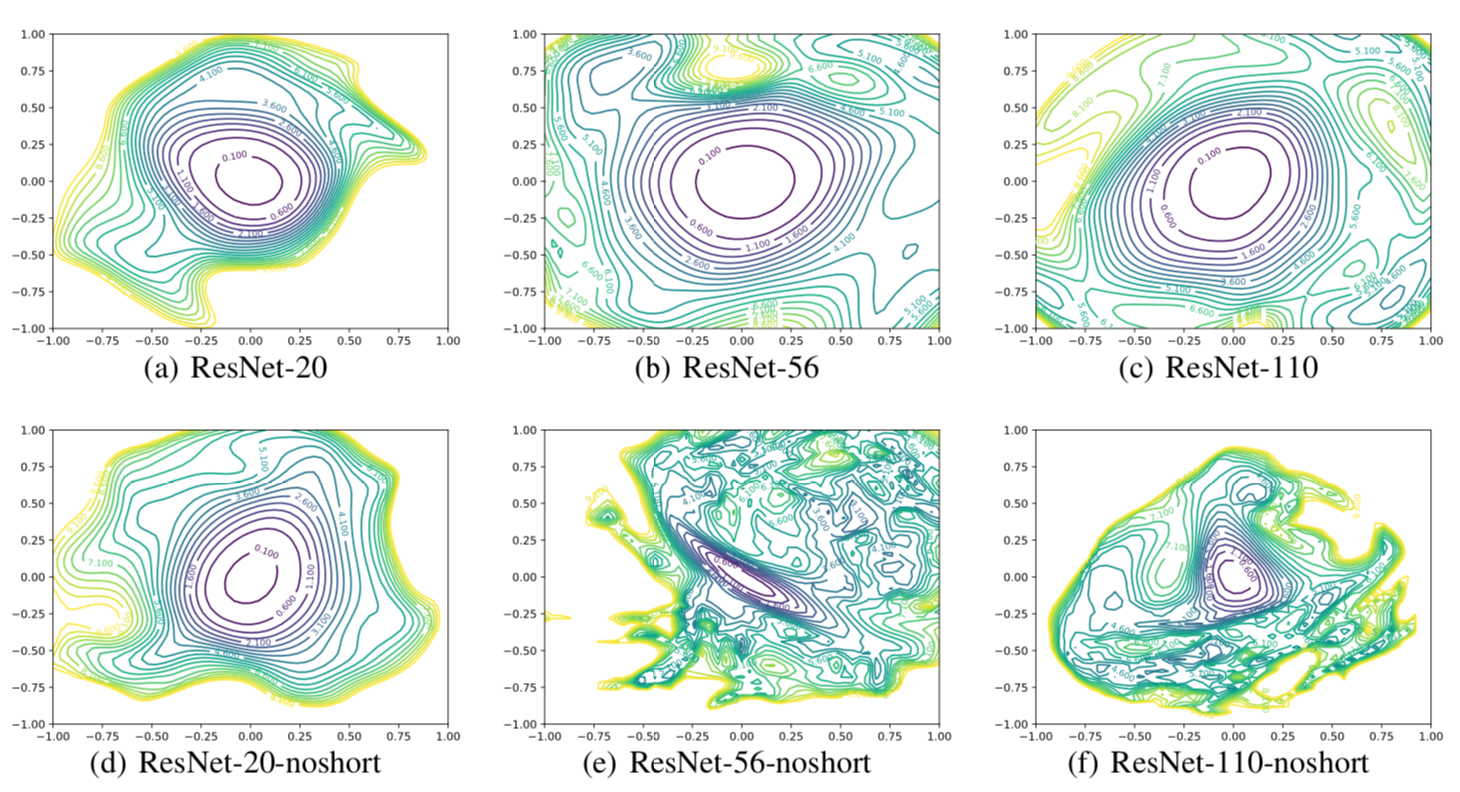
下の学習結果からも、ショートカット無し版では深さに伴い精度が低下していますが、ショートカットあり版では深さにともない精度も向上しています。

4-3.CNNのフィルタ数による影響の可視化
ResNet56のショートカットあり版に対して、各層のCNNのフィルタ数を$k倍$した結果を可視化したのが下の図です。$k$の隣の$%$はテストのエラー率です。
CNNのフィルタ数を増やせば増やすほどロス関数が勾配の緩やかな凸関数に近づき精度も向上していることが見て取れいます。

5. 個人的な感想
アーキテクチャやパラメータの違いによる影響が、可視化されたロス関数の形状に綺麗に反映されているところが面白いです。学習が進まないモデルではロス関数が非凸関数となるのはわかるのですが、その場合どうすれば凸関数にできるかはモデル毎に考える必要がありそうです。
今回は紹介しきれませんでしたがGPUの並列処理の実装方法なども今後の参考になりそうです。
6. (追記)重みの更新
説明が不足しているようなので参考までにFILTER-WISE NORMALIZATIONの重みの更新処理を載せておきます。
各層のランダムな重みの変化を方向ベクトルとして扱っています。そのため原点から特定の方向に移動した場合は、学習完了地点の重みに対してベクトルの移動方向分に相当する重みを加算します。この加算された重みを元にロス関数の計算を行います。
# init_weightsは原点(つまり学習完了状態での)重み
def overwrite_weights(model, init_weights, directions, step):
# dxおよびdyは2つの方向ベクトル
dx = directions[0]
dy = directions[1]
changes = [d0 * step[0] + d1 * step[1] for (d0, d1) in zip(dx, dy)]
device = 'cuda' if torch.cuda.is_available() else 'cpu'
for (p, w, d) in zip(model.parameters(), init_weights, changes):
p.data = w.to(device) + torch.Tensor(d).to(device)
-
モデルの学習完了後のcaluculate_loss_landscape()メソッド内において、'NoneType'関連の例外が発生します。保存されたtrain_modelを読み込めば成功するのでもう一度src.mainを実行してください。 ↩